算法 - 排序

发表于 | 分类于 | 阅读次数

经典排序算法：选择排序、插入排序、希尔排序、归并排序、冒泡排序、快速排序和堆排序。

通用 API

排序算法中的通用 API ： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
// 比较并返回较小值
private static boolean less(Comparable v, Comparable w) {
    return v.compareTo(w) < 0;
}

// is v < w ?
private static boolean less(Object v, Object w, Comparator comparator) {
    return comparator.compare(v, w) < 0;
}

// 交换数组中第 i 和 j 中的元素
// exchange a[i] and a[j]
private static void exch(Object[] a, int i, int j) {
    Object swap = a[i];
    a[i] = a[j];
    a[j] = swap;
}

选择排序

定义

选择排序 Selection sort：遍历数组找到数组中的最小元素，将它和数组中的第一个元素交换位置；其次，在剩下的元素中找到最小的元素，将它与数组的第二个元素交换位置；如此反复直到整个数组排完序。
核心思路：不断的在数组的剩余元素中找出最小的，所以称为选择排序。

动图演示

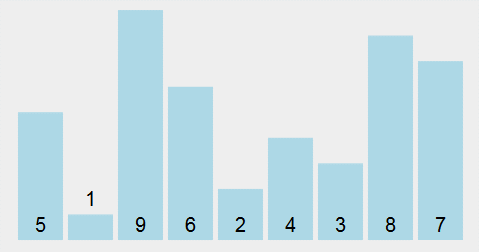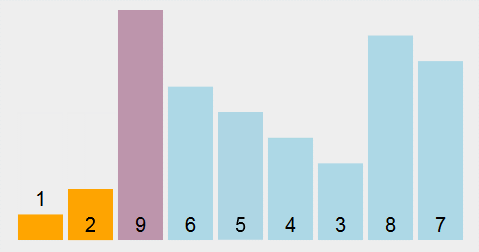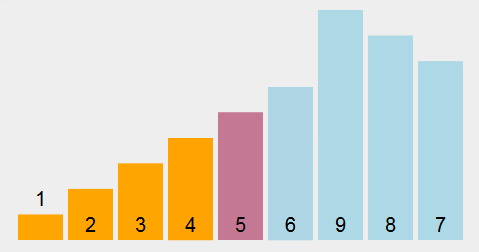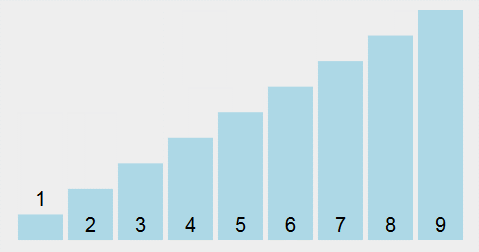
0086-selection-sort.gif

代码示例

1
2
3
4
5
6
7
8
9
10
public static void selection_sort(Comparable[] a) {
    int n = a.length;
    for (int i = 0; i < n; i++) {
        int min = i;
        for (int j = i+1; j < n; j++) {
            if (less(a[j], a[min])) min = j;
        }
        exch(a, i, min);
    }
}

特点

  • 时间复杂度
    根据估算法则，两个嵌套 for 循环，时间复杂度为 O(N²) 。
  • 运行时间和输入无关
    为了找出最小元素扫描一遍数组并不能为下一次扫描提供任何帮助信息，所以和输入数据的初始状态无关。
  • 数据移动最少
    在比较时，如果第一个元素就是最小元素也会和自己交换，所以数组中每个元素都会发生一次交换，整个算法交换次数为 N 。

插入排序

定义

插入排序 Insertion sort：一个已经有序的数据序列，要求在这个已经排好的数据序列中插入一个数，但要求插入后此数据序列仍然有序。
通常说的插入排序为直接插入排序，其核心思想为：将数组分为两部分，第一个为第一部分，将数组剩余元素划为第二部分。将第二部分中的第一个元素取出，和已经排好序的第一部分比较，插入合适的位置。以此类推，直到最后一个元素插入前面已经排好序的数组中。

动图演示

0086-insertion-sort.gif

代码示例

1
2
3
4
5
6
7
8
public static void insertion_sort(Comparable[] a) {
    int n = a.length;
    for (int i = 0; i < n; i++) {
        for (int j = i; j > 0 && less(a[j], a[j-1]); j--) {
            exch(a, j, j-1);
        }
    }
}

特点

  • 时间复杂度
    根据估算法则，两个嵌套 for 循环，时间复杂度为 O(N²) 。
  • 和输入序列高度相关
    如果输入序列是有序的，或者部分有序的，插入排序将会减少很多次比较和交换。最好情况的完全有序，只需要比较 N-1 次。
  • 排序方式
    排序通常是从后向前比较，方便数组移动。
  • 适用范围
    部分有序数组、小规模数组。

希尔排序

定义

希尔排序 Shell sort：是插入排序的一种，又称缩小增量排序，是直接插入排序算法的一种更高效的改进版本。
希尔排序是基于插入排序的以下两点性质而提出改进方法的：

  • 插入排序在对几乎已经排好序的数据操作时，效率高，即可以达到线性排序的效率
  • 但插入排序一般来说是低效的，因为插入排序每次只能将数据移动一位

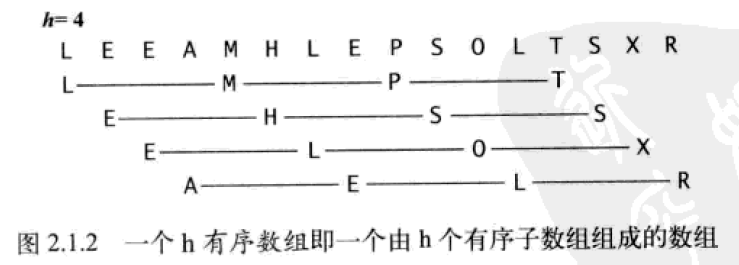
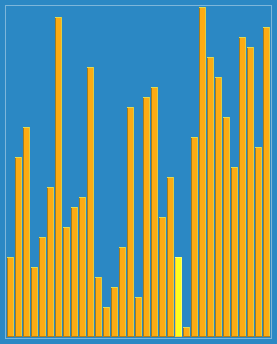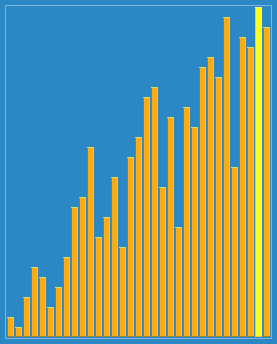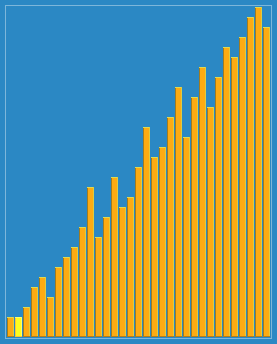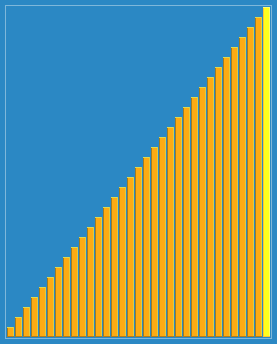
希尔排序核心思想：使数组中任意间隔为 h 的元素是有序的，这样的数组称为：h 有序数组。对于任意以 1 结尾的 h 序列，我们都能将数组排序。其中 h 序列的典型序列满足：h=3h+1 (h<n/3)，如：1, 4, 13, 40, 121, 364, 1093, …
按照不同步长对元素进行插入排序：当刚开始元素很无序的时候，步长最大，所以插入排序的元素个数很少，速度很快；当元素基本有序了，步长很小，插入排序对于有序的序列效率很高。下图为 h 序列展示，希尔排序会对每个 h 序列单独排序，直到 h=1。

0086-shell-sort-h-sequence.png

动图演示

0086-shell-sort.gif

代码示例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public static void shell_sort(Comparable[] a) {
    int n = a.length;

    // 3x+1 increment sequence:  1, 4, 13, 40, 121, 364, 1093, ... 
    int h = 1;
    while (h < n/3) h = 3*h + 1; 

    while (h >= 1) {
        // h-sort the array
        for (int i = h; i < n; i++) {
            for (int j = i; j >= h && less(a[j], a[j-h]); j -= h) {
                exch(a, j, j-h);
            }
        }
        h /= 3;
    }
}

特点

  • 时间复杂度
    按照 3x+1 递增序列，希尔排序的复杂度能达如下量级。希尔排序比选择排序、插入排序速度快得多，数组越大优势越明显。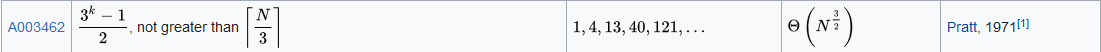
    0086-shell-sort-time-complexity.png
  • 适用范围
    无序数组、中等规模数组。

归并排序

定义

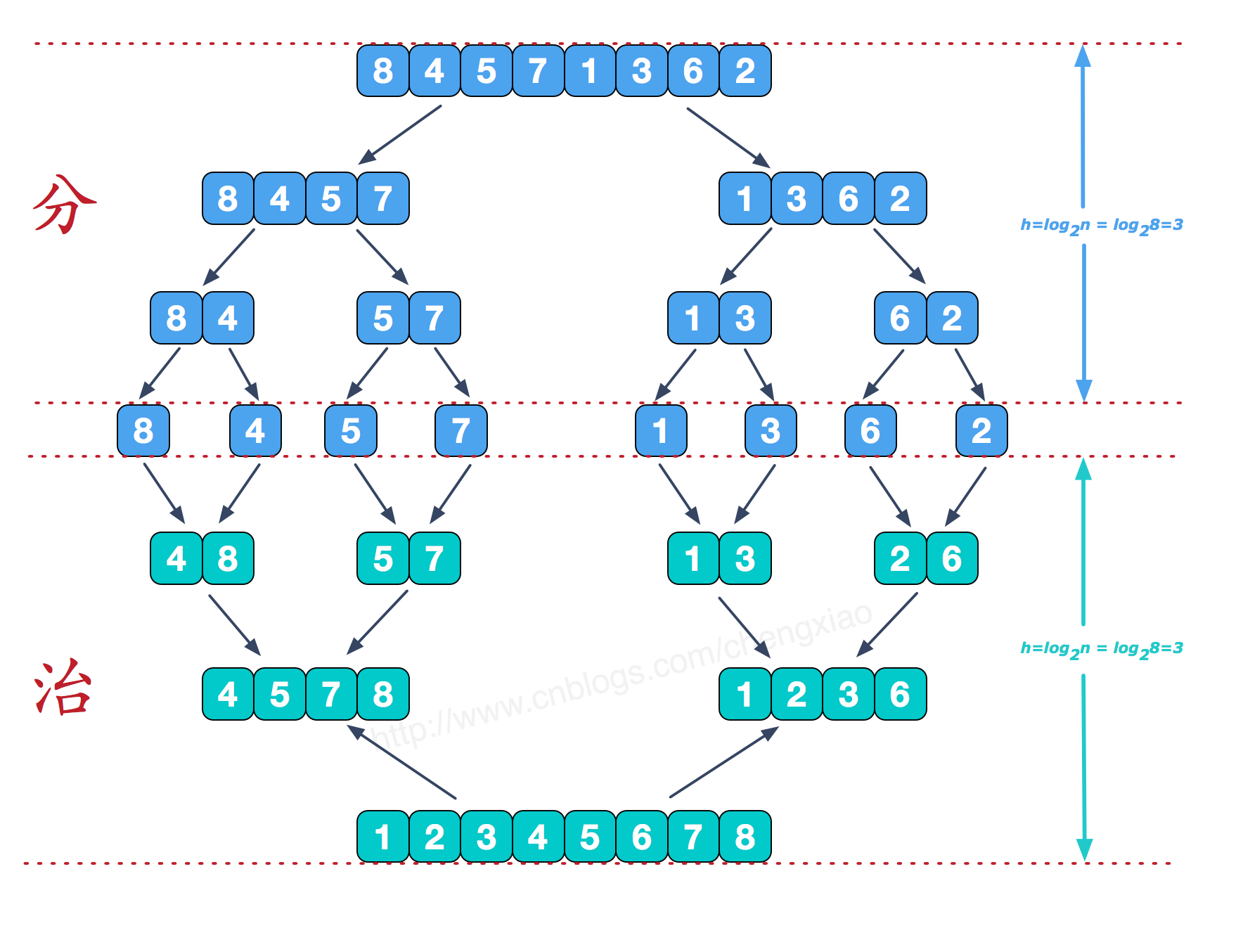
归并排序 Merge sort：该算法是采用分治法 Divide and Conquer 的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。其递归思路：一个数组可以递归地将它分为两半分别排序，然后将结果归并起来。

动图演示

0086-merge-sort.gif

图解

0086-merge-sort-static.png

代码示例

有两种实现方式：递归，自顶向下；非递归，自底向上。

  • 自顶向下，递归方法 

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    /**
     * Rearranges the array in ascending order, using the natural order.
     * @param a the array to be sorted
     */
    public static void sort(Comparable[] a) {
        Comparable[] aux = new Comparable[a.length];
        sort(a, aux, 0, a.length-1);
    }

    // mergesort a[lo..hi] using auxiliary array aux[lo..hi]
    private static void sort(Comparable[] a,Comparable[] aux,int lo,int hi){
        if (hi <= lo) return;
        int mid = lo + (hi - lo) / 2;
        // 递归排序左半部分
        sort(a, aux, lo, mid);
        // 递归排序右半部分
        sort(a, aux, mid + 1, hi);
        // 归并  
        merge(a, aux, lo, mid, hi);
    }

    // 归并过程  
    private static void merge(Comparable[] a, Comparable[] aux, 
        int lo, int mid, int hi) {
        // copy to aux[]
        // 辅助数组
        for (int k = lo; k <= hi; k++) {
            aux[k] = a[k]; 
        }

        // merge back to a[]
        int i = lo, j = mid+1;
        for (int k = lo; k <= hi; k++) {
            if      (i > mid)              a[k] = aux[j++];
            else if (j > hi)               a[k] = aux[i++];
            else if (less(aux[j], aux[i])) a[k] = aux[j++];
            else                           a[k] = aux[i++];
        }
    }

  • 自底向上，非递归 

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    /**
     * Rearranges the array in ascending order, using the natural order.
     * @param a the array to be sorted
     */
    public static void sort(Comparable[] a) {
        int n = a.length;
        Comparable[] aux = new Comparable[n];
        for (int len = 1; len < n; len *= 2) {
            for (int lo = 0; lo < n-len; lo += len+len) {
                int mid  = lo+len-1;
                int hi = Math.min(lo+len+len-1, n-1);
                merge(a, aux, lo, mid, hi);
            }
        }
    }

    private static void merge(Comparable[] a, Comparable[] aux, 
        int lo, int mid, int hi) {
        // copy to aux[]
        for (int k = lo; k <= hi; k++) {
            aux[k] = a[k]; 
        }

        // merge back to a[]
        int i = lo, j = mid+1;
        for (int k = lo; k <= hi; k++) {
            if      (i > mid)              a[k] = aux[j++];
            else if (j > hi)               a[k] = aux[i++];
            else if (less(aux[j], aux[i])) a[k] = aux[j++];
            else                           a[k] = aux[i++];
        }

    }

特点

  • 时间复杂度
    根据归并排序的静态分解图可知，归并排序的结构类似一个二叉树，树的高度就是拆分比较的次数 LogN，而归并比较需要 N 次，所以归并排序的时间复杂度为 O(NlogN) 。

冒泡排序

定义

冒泡排序 Bubble sort：它重复地走访过要排序的元素列，一次比较两个相邻的元素，如果他们的顺序错误就把他们交换过来，重复地进行直到没有相邻元素需要交换。
核心思路：依次比较相邻的两个数，将小数放在前面，大数放在后面。

动图演示

0086-bubble-sort.gif

代码示例

1
2
3
4
5
6
7
8
public void sort(int[] a){
    int n = a.length;
    for(int i=n-1; i>=0; i--){
        for(int j=1; j<=i; j++){
            if(a[j] < a[j-1]) exch(a, j, j-1);
        }
    }
}

特点

  • 时间复杂度
    根据估算法则，两个嵌套 for 循环，时间复杂度为 O(N²) 。
  • 和输入序列高度相关

快速排序

定义

快速排序 Quick sort：是对冒泡排序的一种改进，通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。
快速排序是应用最广泛的排序算法，实现简单且比其他排序算法快的多。

切分

切分 partition：快速排序在数据分割时，切分的位置取决于数组的内容。切分整个过程使得数组满足下面三个条件：

  • 对于某个切分 j，a[j] 位置已经排定
  • a[low] 到 a[j-1] 中的所有元素都不大于 a[j]
  • a[j] 到 a[high] 中的所有元素都不小于 a[j]

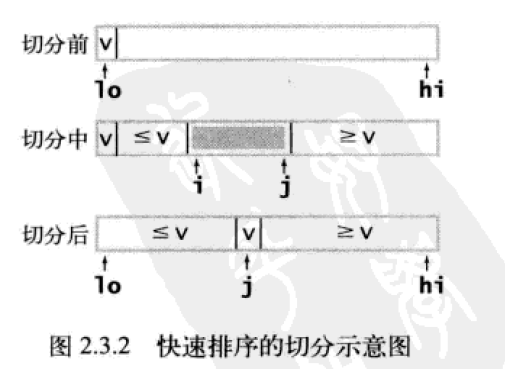
0086-quick-sort-partition.png

切分的策略通常是：

  • 随意地取 a[low] 作为切分元素，该元素将会是被排定的元素
  • 数组从左向右扫描，找到一个大于等于它的元素 a[i]
  • 数组从右向左扫描，找到一个小于等于它的元素 a[j]
  • 如果 i>=j ，表示数组已经有序，退出循环
  • 否则，交换上面两个元素，保证小的元素都在左边，大的元素都在右边
  • 如此反复，直到循环退出后，交换 a[low], a[j] ，并返回 j，切分完毕

动图演示

图示快速排序是从左到右扫描，并同时记录下第一个较大元素，和第一个较小元素交换。

0086-quick-sort.gif

代码示例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
// partition the subarray a[lo..hi] so that a[lo..j-1] <= a[j] <= a[j+1..hi]
// and return the index j.
private static int partition(Comparable[] a, int lo, int hi) {
    int i = lo;
    int j = hi + 1;
    Comparable v = a[lo];
    while (true) { 

        // find item on lo to swap
        while (less(a[++i], v)) {
            if (i == hi) break;
        }

        // find item on hi to swap
        while (less(v, a[--j])) {
            if (j == lo) break;     // redundant since a[lo] acts as sentinel
        }

        // check if pointers cross
        if (i >= j) break;

        exch(a, i, j);
    }

    // put partitioning item v at a[j]
    exch(a, lo, j);

    // now, a[lo .. j-1] <= a[j] <= a[j+1 .. hi]
    return j;
}

public static void sort(Comparable[] a) {
    // 随机打乱输入顺序
    StdRandom.shuffle(a);
    // 递归排序
    sort(a, 0, a.length - 1);
}

// 递归实现版本
// quicksort the subarray from a[lo] to a[hi]
private static void sort(Comparable[] a, int lo, int hi) { 
    if (hi <= lo) return;
    int j = partition(a, lo, hi);
    sort(a, lo, j-1);
    sort(a, j+1, hi);
}

// 非递归实现版本  
// 使用栈来记录递归过程，这种方法多出一个记录栈，
// 而且还需要装箱拆箱，并不是特别好的方法
private void sortNonRecur(int[] a, int low, int high){
    if(high <= low) return;
    Stack<Integer> stack = new Stack<>();
    stack.push(high);
    stack.push(low);
    int i,j,p;
    
    while(!stack.empty()){
        i = stack.pop();
        j = stack.pop();
        p = partition(a, i, j);

        if(p < j){
            stack.push(j);
            stack.push(p+1);
        }

        if(p > i){
            stack.push(p-1);
            stack.push(i);
        }
    }
}

特点

  • 时间复杂度
    快速排序使用了分治思想 logN，而一次切分比较最多 N 次，所以复杂度估算为 NlogN 。
  • 快速排序和归并排序的异同
    归并排序为先递归排序再归并；而快速排序为先切分排序再递归。
  • 不适用小数组，通常在快速排序中，如果小数组直接切换为插入排序

快速排序平均时间复杂度推算：
0086-quick-sort-time-complexity.jpg

三向切分快速排序

对于普通快速排序，如果重复元素很多，这些重复元素的比较和交换都是无任何意义的。三向切分思路是：将数组切分为三部分，分别对应于小于、等于和大于切分元素。

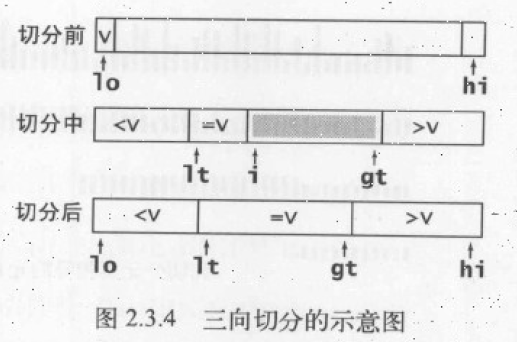
0086-quick-sort-3-way.png

三向切分快速排序实现步骤：从左向右遍历一遍数组，维护一个指针 lt 使得 a[low..lt-1] 中的元素都小于 v，一个指针 gt 使得 a[gt+1..high] 中的元素都大于 v ，一个指针 i 使得 a[lt..i-1] 中的元素都等于 v，a[i..gt] 中的元素未排序，直到 i>gt 即 a[i..gt] 为空，所有元素排序完毕，遍历结束。

  • 指定 a[low] 元素为切分元素 v，i,lt,low 相等同时指向 v
  • gt,high 相等，即 gt 指向数组最后一个元素
  • 如果 a[i] 小于 v，将 a[lt] 和 a[i] 交换，将 lt, i 分别加 1
  • 如果 a[i] 大于 v，将 a[gt] 和 a[i] 交换，将 gt 减 1
  • 如果 a[i] 等于 v，将 i 加 1

对拥有重复元素的数组，三向切分能大大提高排序速度。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
public static void sort(Comparable[] a) {
    // 随机打乱输入顺序
    StdRandom.shuffle(a);
    sort(a, 0, a.length - 1);
}

// quicksort the subarray a[lo .. hi] using 3-way partitioning
private static void sort3Way(Comparable[] a, int lo, int hi) { 
    if (hi <= lo) return;
    // 初始化 lt,gt,i
    int lt = lo, gt = hi;
    Comparable v = a[lo];
    int i = lo + 1;
    while (i <= gt) {
        int cmp = a[i].compareTo(v);
        if      (cmp < 0) exch(a, lt++, i++);
        else if (cmp > 0) exch(a, i, gt--);
        else              i++;
    }

    // a[lo..lt-1] < v = a[lt..gt] < a[gt+1..hi]. 
    // 递归调用
    sort(a, lo, lt-1);
    sort(a, gt+1, hi);
}

排序算法的稳定性

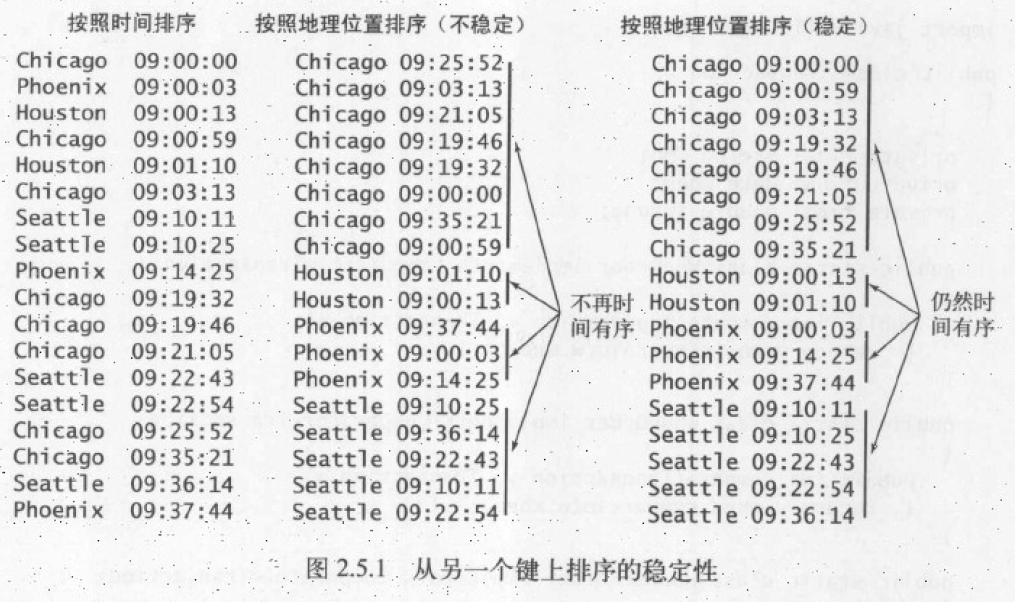
稳定性：如果一个排序算法能够保留数组中的已排好序元素的相对位置则可以被称为稳定的。也就是说排序算法在执行的过程中，对于已经排好序的元素，不会再次打乱，就是稳定的排序算法。

  • 插入排序和归并排序是稳定的；选择排序、希尔排序、快速排序和堆排序都不是稳定的。
  • 稳定性的意义是，可以多键值排序，后面键值的排序不会打乱前面已经排过序的键值。比如一张表先按时间排序，再按名称排序。稳定性算法排完名称后，相同名称的数据，仍然会按照时间排序。

0086-sort-stability.png

排序算法性能

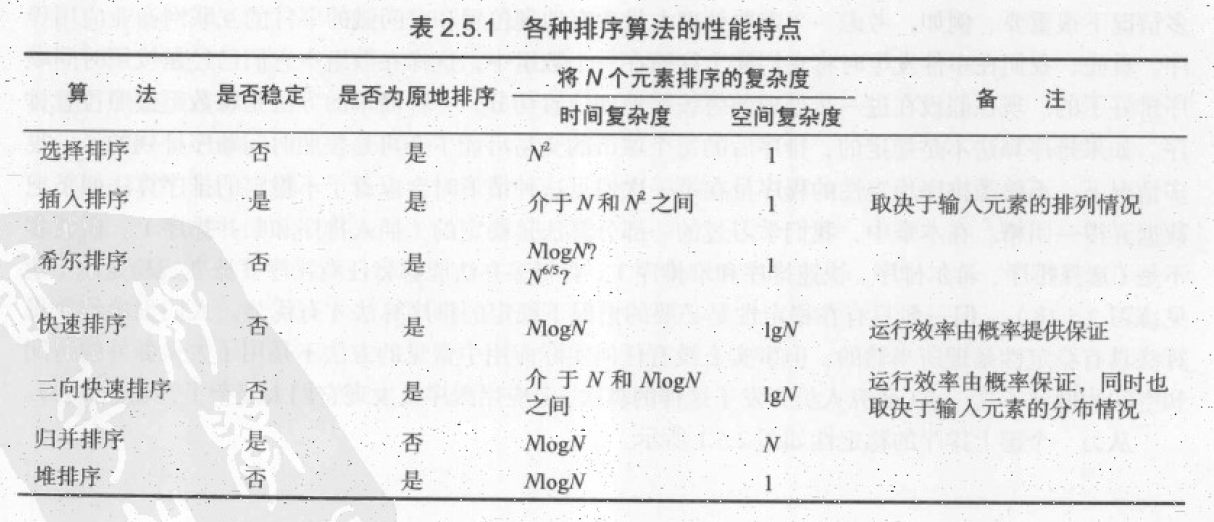
0086-sort-performance.png

从图中可以看出，快速排序性能是最优的。JDK 中数组排序使用的是 DualPivotQuicksort.java，后续再介绍这种双轴排序算法。源码可以看出通常当被排序数组很小时，使用插入排序；大数组直接使用快速排序。

参考文档

0%