算法 - 优先队列 - 二叉堆

发表于 | 分类于 | 阅读次数

算法：优先队列、堆、二叉堆、索引优先队列、堆排序等相关介绍。

基本概念

定义

优先队列 Priority queue ：是这样一种数据结构，支持删除优先级最高元素和插入元素。通常有两种实现方式：

  • 最大优先队列：支持删除最大元素
  • 最小优先队列：支持删除最小元素

通用 API

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
public class MaxPQ<Key> implements Iterable<Key> {
    // 存储优先队列的元素
    private Key[] pq;                    // store items at indices 1 to n
    // 优先队列长度
    private int n;                       // number of items on priority queue
    // 各种构造方法
    public MaxPQ(int initCapacity) {...}
    public MaxPQ() {...}
    public MaxPQ(int initCapacity, Comparator<Key> comparator) {...}
    public MaxPQ(Comparator<Key> comparator) {...}
    public MaxPQ(Key[] keys) {...}
    public boolean isEmpty() {...}
    public int size() {...}
    // 返回最大元素
    public Key max() {...}
    // 动态调整优先队列数组大小，以 2 的倍数调整
    private void resize(int capacity) {...}
    // 插入元素
    public void insert(Key x) {...}
    // 删除最大元素，并返回最大值
    public Key delMax() {...}
    // 上浮
    private void swim(int k) {...}
    // 下沉
    private void sink(int k) {...}

   /********************************************************************
    * Helper functions for compares and swaps.
    ********************************************************************/
    // 最大优先队列和最小优先队列，主要是在比较上返回值相反
    private boolean less(int i, int j) {
        if (comparator == null) {
            return ((Comparable<Key>) pq[i]).compareTo(pq[j]) < 0;
        }
        else {
            return comparator.compare(pq[i], pq[j]) < 0;
        }
    }

    private void exch(int i, int j) {
        Key swap = pq[i];
        pq[i] = pq[j];
        pq[j] = swap;
    }
}

优先队列的初级实现

  • 数组实现无序
    插入元素：直接插入到数组最后一列；删除最大元素：遍历数组找到最大元素，和最后一列交换后删除它。
  • 数组实现有序
    插入元素：类似插入排序，将所有较大元素向右移动一格使数组保持有序；删除元素：最大元素总是在数组最右边，直接删除。
  • 链表实现
    可以基于链表模拟栈操作，pop 找到并返回最大元素并删除；push 保证元素为逆序。

0087-priority-queue-array.png

0087-priority-queue-implement.png

二叉堆

堆

堆 Heap 是一类特殊的数据结构的统称，堆通常是一个可以被看做一棵树的数组对象。堆总是满足下列性质：

  • 堆中某个节点的值总是不大于或不小于其父节点的值
  • 堆总是一棵完全二叉树

堆的定义如下：n 个元素的序列 {K1,K2,Ki,…,Kn} 当且仅当满足下关系时，称之为堆：

  • (Ki <= K2i,ki <= K2i+1) 或者 (Ki >= K2i,Ki >= K2i+1), (i = 1,2,3,4...n/2)
  • 若将和此次序列对应的一维数组（即以一维数组作此序列的存储结构）看成是一个完全二叉树，则堆的含义表明：完全二叉树中所有非终端结点的值均不大于（或不小于）其左、右孩子结点的值。由此，若序列 {K1,K2,…,Kn} 是堆，则堆顶元素（或完全二叉树的根）必为序列中 n 个元素的最小值（或最大值）

将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。
堆有序：当一颗二叉树的每个节点都大于等于它的两个子节点时，称为堆有序。
常见的堆有：二叉堆、二项堆、斐波那契堆。本文重点介绍二叉堆。

二叉堆

二叉堆 binary heap 是一种特殊的堆。二叉堆是：完全二叉树或者是近似完全二叉树。二叉堆有两种：

  • 最大堆
    父结点的键值总是大于或等于任何一个子节点的键值。
  • 最小堆
    父结点的键值总是小于或等于任何一个子节点的键值。

二叉堆定义：一组能够用堆有序的完全二叉树排序的元素，并在数组中按照层级存储（不使用数组的第一个位置）。
二叉堆在数组中的数学性质：

  • 位置为 k 的节点，其父节点位置为向下取整 [k/2] ，其两个子节点位置为 2k,2k+1
  • 位置为 k 的节点，在数组中向上移动一层时，则令 k=2/k；向下移动一层，则令 k=2k 或者 k=2k+1

本文中，默认堆数组的第 0 个元素不保留任何信息，从第 1 个元素开始存储堆元素。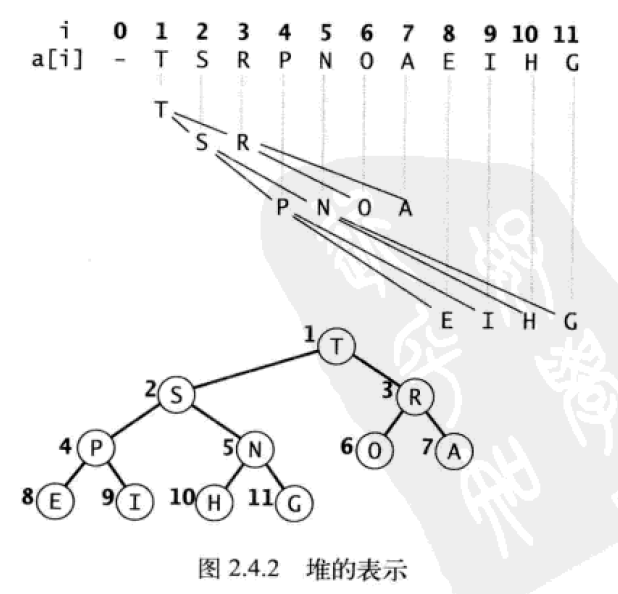
0087-binary-heap-show.png

二叉堆有序化

二叉堆的插入和删除操作会打破堆的状态，需要遍历整个堆并按照要求将堆的状态恢复，称为堆的有序化。

上浮

上浮 swim ：由下至上的堆有序化。如果堆的有序状态因为某个节点变得比它的父节点更大而打破，那么需要交换它和它的父节点来修复堆。但是交换后，该节点可能仍然比父节点大，因此需要重复比较，将这个节点不断的上移，直到找到更大的父节点。这个节点每次都需要上浮到堆的上一层，直到堆恢复有序状态。

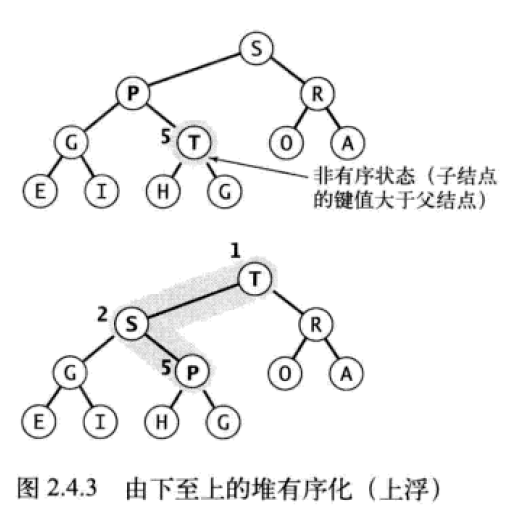
0087-binary-heap-swim.png

1
2
3
4
5
6
private void swim(int k) {
    while (k > 1 && less(k/2, k)) {
        exch(k, k/2);
        k = k/2;
    }
}

下沉

下沉 sink ：由上至下的堆有序化。如果堆的有序状态因为某个节点变得比它的两个子节点或者其中一个子节点更小而打破，那么需要交换它和较大子节点来修复堆。同样，交换后该节点可能仍然比子节点或者其中一个子节点小，因此需要重复比较，将这个节点不断的下移，直到找到它的子节点都比它小或者堆的底部。这个节点每次都需要下沉到堆的下一层，直到堆恢复有序状态。

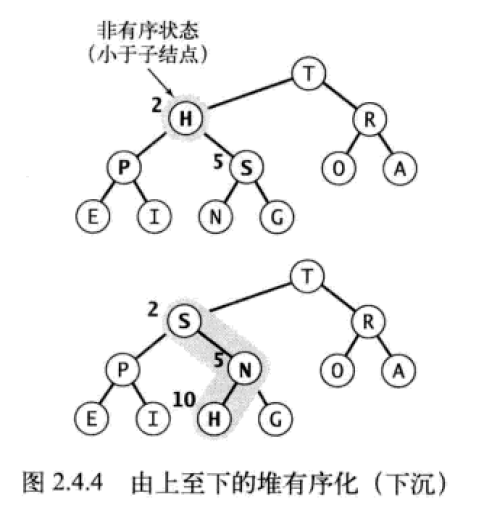
0087-binary-heap-sink.png

1
2
3
4
5
6
7
8
9
10
11
12
private void sink(int k) {
    while (2*k <= n) {
        // 找出较大的子节点
        int j = 2*k;
        if (j < n && less(j, j+1)) j++;
        // 比较如果节点比较大子节点大，下沉结束
        if (!less(k, j)) break;
        // 否则和较大子节点交换
        exch(k, j);
        k = j;
    }
}

插入和删除最大元素

  • 插入元素
    将新元素加入到数组末尾，并让这个新元素上浮到合适位置。
  • 删除最大元素
    从数组顶端删除最大元素（根元素），将数组的最后一个元素放到顶端，并将这个元素下沉到合适位置。

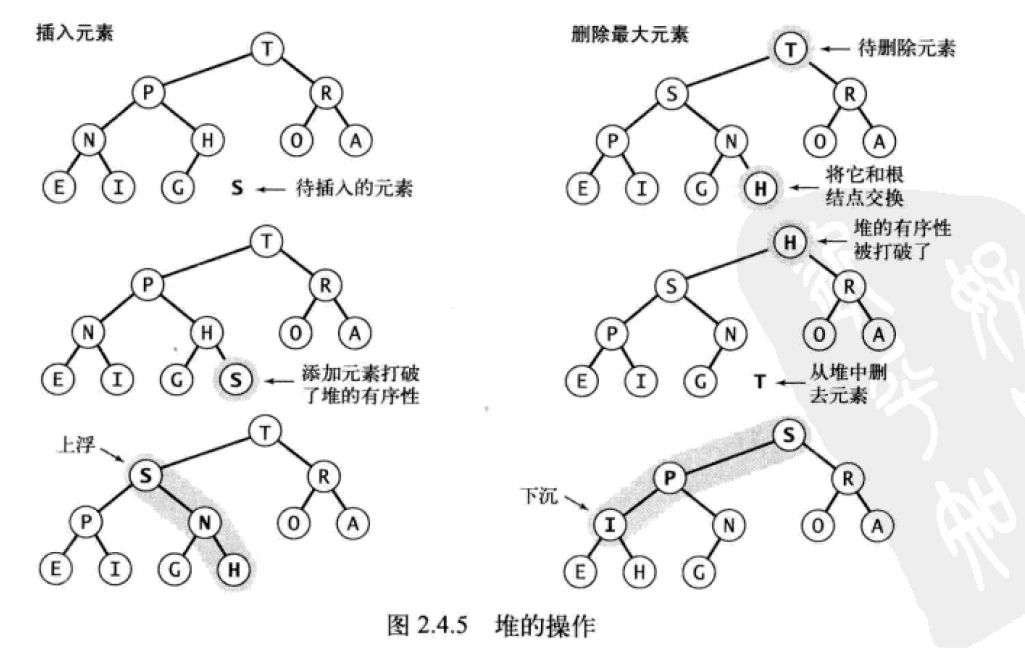
0087-binary-heap-insert-delmax.png

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
public void insert(Key x) {

    // double size of array if necessary
    // 检查优先队列大小，是否需要扩容
    if (n == pq.length - 1) resize(2 * pq.length);

    // add x, and percolate it up to maintain heap invariant
    // 将新元素加入到数组末尾
    pq[++n] = x;
    
    // 将新元素上浮到合适位置
    swim(n);
}

public Key delMax() {
    // 判断优先队列是否为空  
    if (isEmpty()) throw 
        new NoSuchElementException("Priority queue underflow");
        
    // 删除优先队列顶端元素，并将最后一个元素交换到顶端
    Key max = pq[1];
    exch(1, n);
    pq[n] = null;     // to avoid loiterig and help with garbage collection
    
    // 将顶端元素下沉到合适位置 
    sink(1);    
    
    // 调整优先队列大小
    if ((n > 0) && (n == (pq.length - 1) / 4)) resize(pq.length / 2);
    return max;
}

根据上面算法的估算，插入和删除最大元素的时间复杂度都是 O(logN)。

二叉堆构造过程

二叉堆的构造过程：逐个插入元素，保持堆的有序状态。

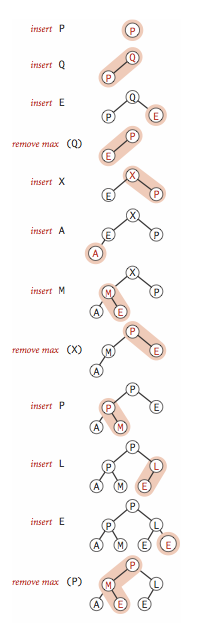
0087-binary-heap-construct.png

小结

可以看出，优先队列在插入元素的过程中，堆始终保持有序状态；删除最大值（最小值），堆仍然有序。优先队列的特点，不需要事先将所有元素读入内存，可以一边读入，一边保持堆有序状态。

索引优先队列

意义

索引优先队列，首先是一个优先队列，但是又带有索引。索引是用来干什么的呢？我们先回顾下上面介绍的优先队列中，Key[] pq 保存了所有元素，并构成二叉堆，并不方便查找指定元素的位置，或者在指定位置更新元素。索引优先队列，使用数组 Key[] keys 存储元素信息（或其他重要信息），增加一个整型数组 int[] pq 来保存元素下标（即索引），使用索引数组构成二叉堆。这样二叉堆在插入，删除，修改时，仅仅改变的是索引数组，而元素数组并不需要变化（删除元素时置空）。通过索引可以找到元素在堆中的下标，再用这个下标就能访问到元素。

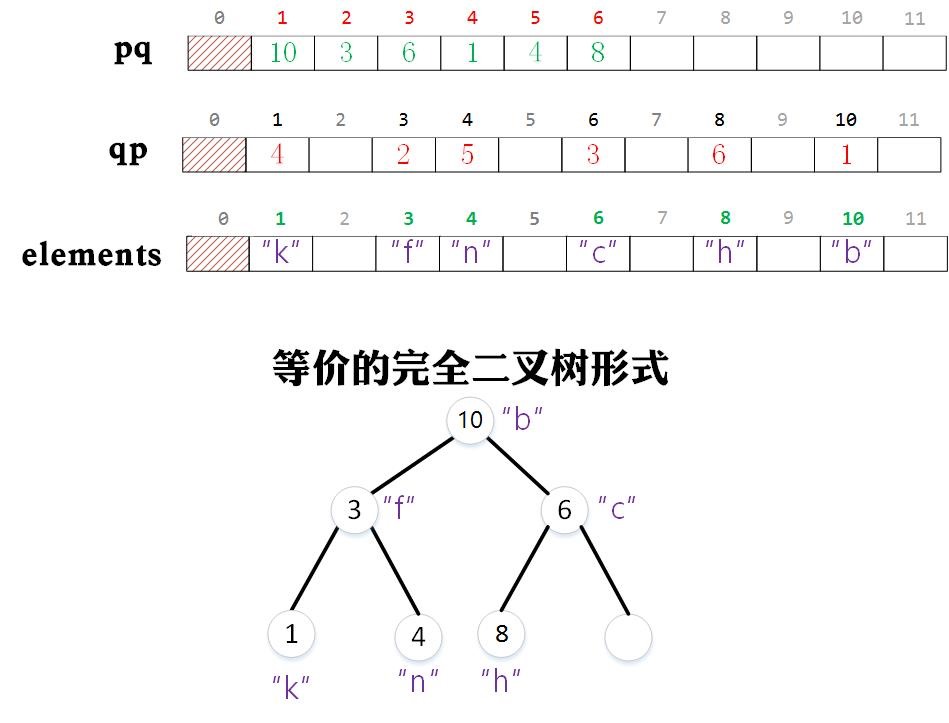
0087-binary-heap-index-priority-queue.jpg

通用 API

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
public class IndexMinPQ<Key extends Comparable<Key>> 
    implements Iterable<Integer> {
    private int maxN;        // maximum number of elements on PQ
    private int n;           // number of elements on PQ
    // pq 存储元素在 keys 中的下标（即索引），并构成二叉树
    private int[] pq;        // binary heap using 1-based indexing
    // qp 存储索引在 pq 中的下标，主要是方便检索 pq。换句话说
    // 元素在 keys 中的下标保存在 pq 中
    // 元素在 keys 中的下标，在 pq 中的下标，保存在 qp 中
    // 某个元素索引满足等式：qp[pq[i]] = pq[qp[i]] = i
    private int[] qp;        // inverse of pq - qp[pq[i]] = pq[qp[i]] = i
    // Key 可以包含很多信息，可以是自定义类
    // 只需要指定排序方式（指定某个属性为优先级，用于排序）
    // 索引优先队列中 Key[] 并不需要交换，也不会移动数据，只需要比较就行
    // 二叉堆建立、插入、删除，都基于索引数组 pq, qp
    private Key[] keys;      // keys[i] = priority of i
    
    public IndexMinPQ(int maxN) {...}
    public boolean isEmpty(){...}
    public int size() {...}
    
    // 索引优先队列，指定索引位置插入元素
    public void insert(int i, Key key) {...}
    // 最小值的索引
    public int minIndex() {... return pq[1];}
    // 最小值元素
    public Key minKey() {... return keys[pq[1]];}
    // 删除最小值
    public int delMin() {...}
    
    public boolean contains(int i) {...}
    public Key keyOf(int i) {... return keys[i];}
    // 指定索引位置，修改元素值
    public void changeKey(int i, Key key) {...}
    public void decreaseKey(int i, Key key) {...}
    public void increaseKey(int i, Key key) {...}
    public void delete(int i) {...}

    /*************************************************************
    * General helper functions.
    **************************************************************/
    // 本示例介绍的是：索引最小优先队列，所以根存放的是最小值
    private boolean greater(int i, int j) {
        return keys[pq[i]].compareTo(keys[pq[j]]) > 0;
    }

    // 仅仅改变索引数组和反向数组
    private void exch(int i, int j) {
        int swap = pq[i];
        pq[i] = pq[j];
        pq[j] = swap;
        qp[pq[i]] = i;
        qp[pq[j]] = j;
    }
    
   /**************************************************************
    * Heap helper functions.
    **************************************************************/
    // 越小越上浮
    private void swim(int k) {
        while (k > 1 && greater(k/2, k)) {
            exch(k, k/2);
            k = k/2;
        }
    }

    // 越大越下沉
    private void sink(int k) {
        while (2*k <= n) {
            int j = 2*k;
            if (j < n && greater(j, j+1)) j++;
            if (!greater(k, j)) break;
            exch(k, j);
            k = j;
        }
    }
}

关键算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
// 插入元素
public void insert(int i, Key key) {
    ...
    n++;
    // 反向数组，记录索引在二叉堆的位置
    qp[i] = n;
    // 索引始终加入到二叉堆最后一列
    pq[n] = i;
    // 在指定索引位置添加元素
    keys[i] = key;
    // 上浮到合适位置
    swim(n);
}

// 删除最小值
public int delMin() {
    ...
    // 最小值始终在二叉堆第一个有效位置
    int min = pq[1];
    // 二叉堆中最小值和最后一个元素交换
    exch(1, n--);
    // 将交换过来的索引下沉到合适位置
    sink(1);
    assert min == pq[n+1];
    // 反向数组，元素数组，对应索引位置置空
    qp[min] = -1;        // delete
    keys[min] = null;    // to help with garbage collection
    pq[n+1] = -1;        // not needed
    return min;
}

// 修改指定索引位置的元素
public void changeKey(int i, Key key) {
    ...
    // 修改元素值
    keys[i] = key;
    // 这里是否可以优化，先比较 key 是变大还是变小了
    // 再来决定是上浮还是下沉
    swim(qp[i]);
    sink(qp[i]);
}

public void delete(int i) {
    ...
    int index = qp[i];
    exch(index, n--);
    swim(index);
    sink(index);
    keys[i] = null;
    qp[i] = -1;
}

小结

  • 时间复杂度
    索引优先队列，不管是插入、删除、修改等，时间复杂度都能控制在 logN，但是需要辅助数组来快速实现。
  • 优点
    除了能多保存元素信息，索引优先队列还可以更新指定索引的 key 值，这个是普通优先队列无法做到的。通常普通优先队列，对外 API 只包含队列的基本操作，只是在取出元素时，确保每次都是取出的最小值或者最大值。

堆排序

定义

堆排序 Heap sort：使用堆数据结构设计的一种排序算法，它是选择排序的一种。利用小根堆或者大根堆的特性，每次选出最小值或者最大值来完成排序。堆排序有两个阶段：

  • 堆构造阶段
    将数据读入后，构造一个堆。堆的特点是，不管什么时候加入新数据，堆都是有序的。
  • 堆下沉阶段（大根堆，由大到小排序）
    始终从堆中取出最大元素，并得到排序结果。取出最大元素后，堆最后一列元素交换到堆顶，并下沉到合适位置，确保堆保持有序。

动图演示

  • 堆构造-插入法
    向优先队列一样，逐个插入新元素来构造堆，这个过程时间复杂度为 NlogN 。
    0087-heap-sort-constuctor.gif

  • 堆构造-原地构造（经典算法）
    现有数组为元素读入顺序，直接在这个数组上构造堆。具体方法：从数组中间位置，从右向左逐个元素 sink 来构造堆，时间复杂度为 N。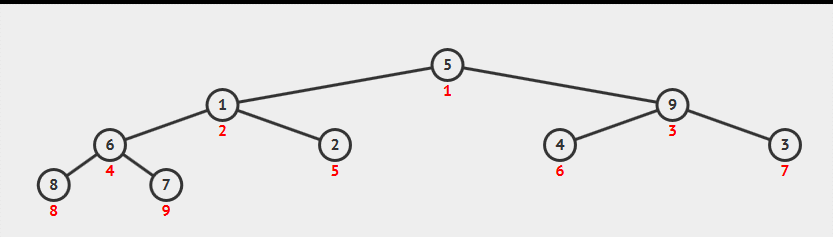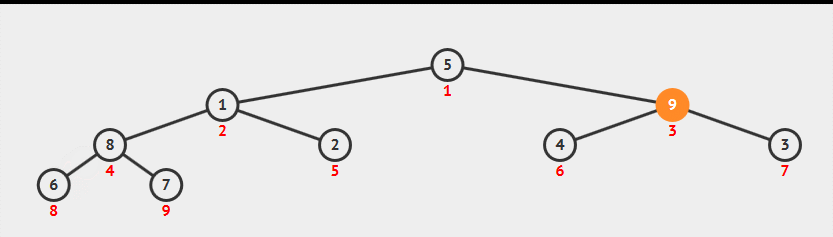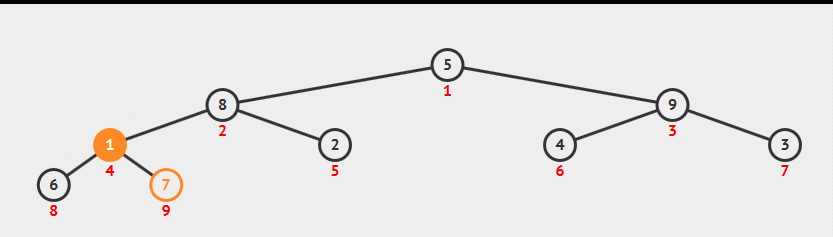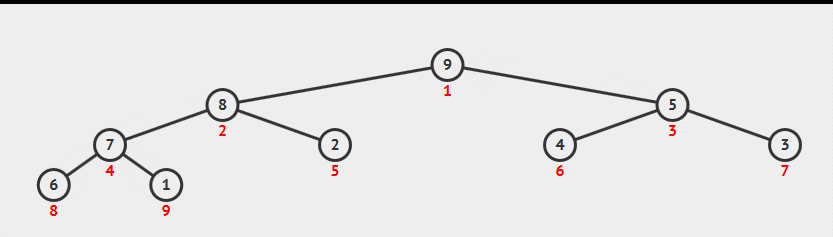
    0087-heap-sort-sink.gif

  • 堆取出最大值
    优先队列，逐个取出最大值，实现排序效果。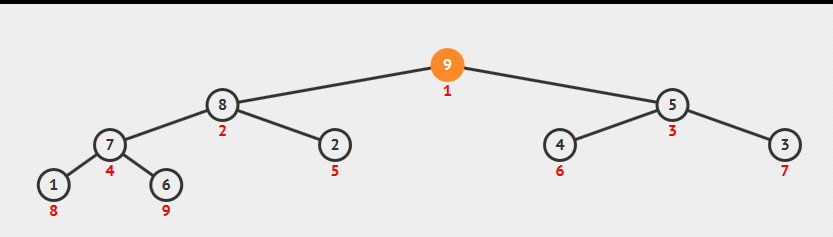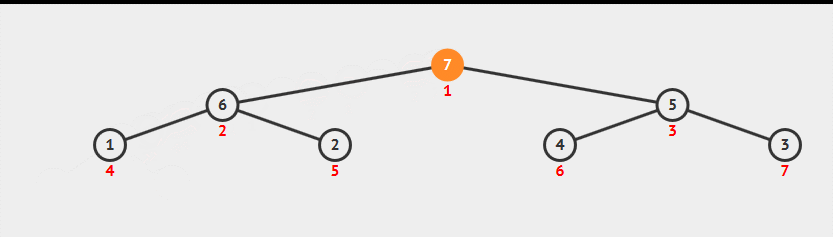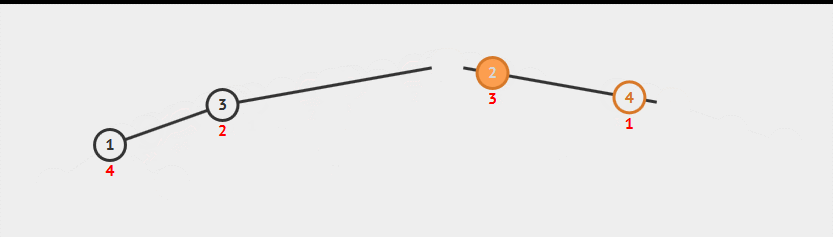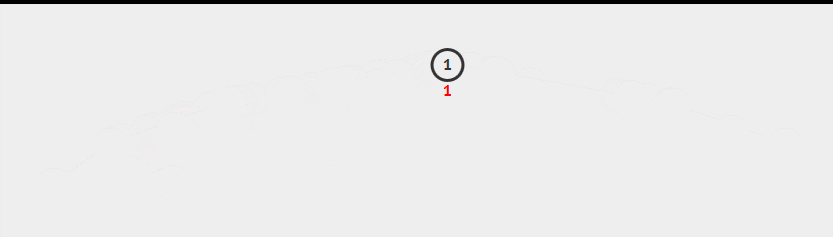
    0087-heap-sort.gif

堆排序经典算法代码示例

我们可以使用优先队列，插入元素方法构造堆，删除最大元素方法来实现堆排序。但是我们接下来介绍的是，使用 sink 下沉方法，来原地构造堆和排序，这种算法就是经典的堆排序算法，由 J.W.Williams 发明，并由 R.W.Floyd 在 1964 年改进。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
public static void sort(Comparable[] a) {
    int n = a.length;
    // 堆构造
    // 核心思路：从数组中间位置，从右向左逐个将元素 sink 来构造堆
    // 也就是从最后一个子堆开始，逐个将子堆有序化
    // 当到最后一个子堆时，也就是整个堆，下沉第一个元素，确保整个堆有序化
    for (int k = n/2; k >= 1; k--)
        sink(a, k, n);
        
    // 堆排序
    while (n > 1) {
        // 核心思路：将最大值交换到数组最后一列
        // 将交换到第一个的元素，在剩下的 n-1 个元素中做下沉
        // 使得 n-1 个元素的堆恢复到有序状态，即始终确保堆第一个元素为最大值
        // 如此反复，直到只剩下第一个元素
        // 整个数组变成有序状态
        exch(a, 1, n--);
        sink(a, 1, n);
    }
}

private static void sink(Comparable[] a, int k, int n) {
    while (2*k <= n) {
        // 找出较大的子节点
        int j = 2*k;
        if (j < n && less(a, j, j+1)) j++;
        
        // 如果比子节点大，跳出
        if (!less(a, k, j)) break;
        
        // 交换，并循环下沉到合适位置
        exch(a, k, j);
        k = j;
    }
}

// 数组从 a[1] 开始为有效元素
private static boolean less(Comparable[] a, int i, int j) {
    return a[i].compareTo(a[j]) < 0;
}

private static void exch(Object[] a, int i, int j) {
    Object swap = a[i];
    a[i] = a[j];
    a[j] = swap;
}

堆排序静态分解图

  • 堆形态分解轨迹
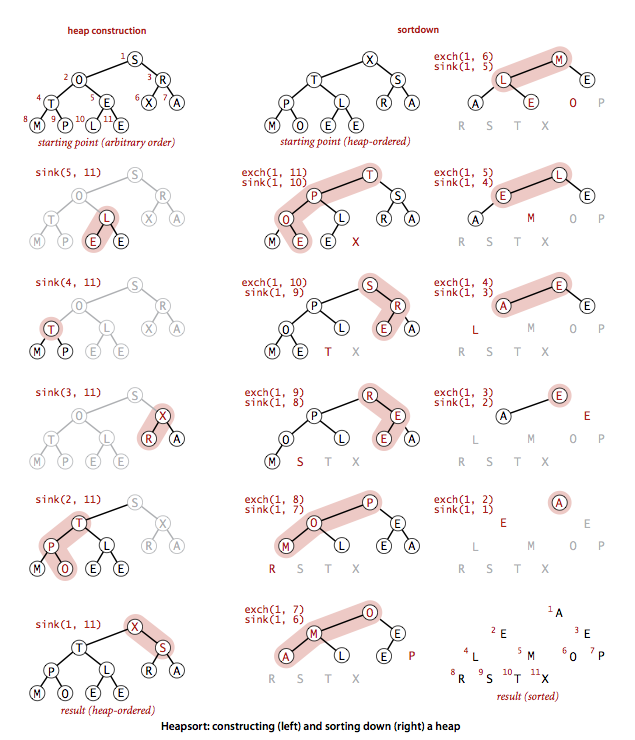
    0087-heapsort-trace.png

  • 数组形态分解轨迹
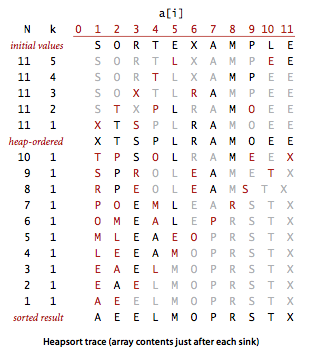
    0087-heapsort-array.png

特点

经典堆排序算法中：

  • 堆构造只需少于 2N 次比较和 N 次交换
  • 堆排序只需要 2NlogN 次比较和 NlogN 次交换
  • 整个堆排序过程为上述之和

JDK 中的优先队列

JDK 中的优先队列源码为 java.util.PriorityQueue.java，默认是最小优先队列（小根堆），如果需要实现最大优先队列，在构造时传入自定义 Comparator 实现大根堆的比较就可以了。

类图结构

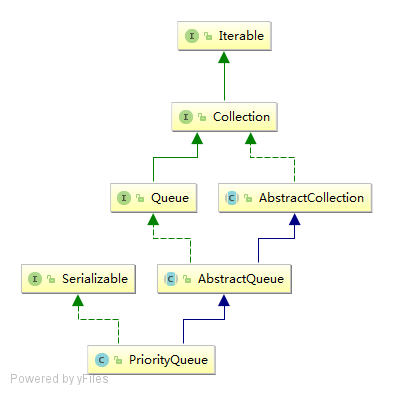
0087-JDK-PriorityQueue-UML.png

源码分析

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
public class PriorityQueue<E> extends AbstractQueue<E>
    implements java.io.Serializable {
    private static final int DEFAULT_INITIAL_CAPACITY = 11;

    // 存储元素数组
    transient Object[] queue; // non-private to simplify nested class access
    // 元素个数
    private int size = 0;
    private final Comparator<? super E> comparator;
    
    // 构造方法
    public PriorityQueue() {...}
    public PriorityQueue(int initialCapacity) {...}
    public PriorityQueue(Comparator<? super E> comparator) {...}
    public PriorityQueue(int initialCapacity,
                         Comparator<? super E> comparator) {...}
    public PriorityQueue(Collection<? extends E> c) {...}
    public PriorityQueue(PriorityQueue<? extends E> c) {...}
    public PriorityQueue(SortedSet<? extends E> c) {...}
    
    // 优先队列中增加一个元素
    public boolean add(E e) {return offer(e);}
    // 数组最后一列加入新元素，并将新元素上浮到合适位置
    public boolean offer(E e) {
        if (e == null)
            throw new NullPointerException();
        modCount++;
        int i = size;
        if (i >= queue.length)
            grow(i + 1);
        size = i + 1;
        if (i == 0)
            queue[0] = e;
        else
            siftUp(i, e);
        return true;
    }
    
    // 取出最小值
    public E peek() {return (size == 0) ? null : (E) queue[0];}
    public boolean remove(Object o) {...}
    public boolean contains(Object o) {...}
    public int size() {...}
    public void clear() {...}
    
    // 取出最小值后，将最后一列元素交换并下沉到合适位置
    public E poll() {
        if (size == 0)
            return null;
        int s = --size;
        modCount++;
        E result = (E) queue[0];
        E x = (E) queue[s];
        queue[s] = null;
        if (s != 0)
            siftDown(0, x);
        return result;
    }
    
    private void siftUp(int k, E x) {
        if (comparator != null)
            siftUpUsingComparator(k, x);
        else
            siftUpComparable(k, x);
    }

    @SuppressWarnings("unchecked")
    // 上浮
    private void siftUpComparable(int k, E x) {
        Comparable<? super E> key = (Comparable<? super E>) x;
        while (k > 0) {
            int parent = (k - 1) >>> 1;
            Object e = queue[parent];
            if (key.compareTo((E) e) >= 0)
                break;
            queue[k] = e;
            k = parent;
        }
        queue[k] = key;
    }

    @SuppressWarnings("unchecked")
    private void siftUpUsingComparator(int k, E x) {...}

    private void siftDown(int k, E x) {
        if (comparator != null)
            siftDownUsingComparator(k, x);
        else
            siftDownComparable(k, x);
    }

    @SuppressWarnings("unchecked")
    // 下沉
    private void siftDownComparable(int k, E x) {
        Comparable<? super E> key = (Comparable<? super E>)x;
        int half = size >>> 1;        // loop while a non-leaf
        while (k < half) {
            int child = (k << 1) + 1; // assume left child is least
            Object c = queue[child];
            int right = child + 1;
            if (right < size &&
                ((Comparable<? super E>) c).compareTo((E) queue[right]) > 0)
                c = queue[child = right];
            if (key.compareTo((E) c) <= 0)
                break;
            queue[k] = c;
            k = child;
        }
        queue[k] = key;
    }

    @SuppressWarnings("unchecked")
    private void siftDownUsingComparator(int k, E x) {...}
}

小结

PriorityQueue 所有公共接口，几乎和队列保持一致。所以可以参考队列的使用方式，但实际的存储是以堆的形式存在的。

参考文档

0%