算法 - 红黑树 | Earth Guardian

算法：2-3 查找树，红黑树，JDK 中 TreeMap 源码分析。其中 2-3 查找树，红黑树基本定义参考《算法 4》，TreeMap 源码解析参考《算法导论》中红黑树的分析。

2-3 查找树

定义

2-3 查找树的定义：一颗 2-3 查找树或为一颗空树，或由以下节点组成：

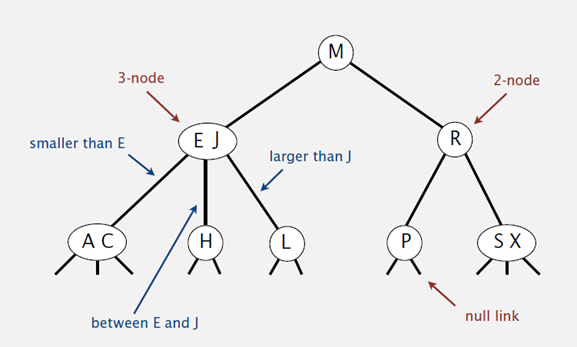
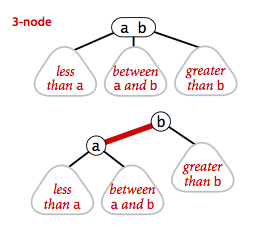
2 节点：含有一个键（及其对应的值）和两条链接，左链接指向的 2-3 树中的键都小于该节点，右链接指向的 2-3 树中的键都大于该节点
3 节点：含有两个键（及其对应的值）和三条链接，左链接指向的 2-3 树中的键都小于该节点，中链接指向的 2-3 树中的键都位于该节点的两个键之间，右链接指向的 2-3 树中的键都大于该节点
空链接：指向一颗空树的链接

一颗完美平衡的 2-3 查找树中，所有的空链接到根节点的距离都是相同的。通常我们在操作（构造、插入、删除）时，都会刻意保持 2-3 树的平衡性，有序性。

查找

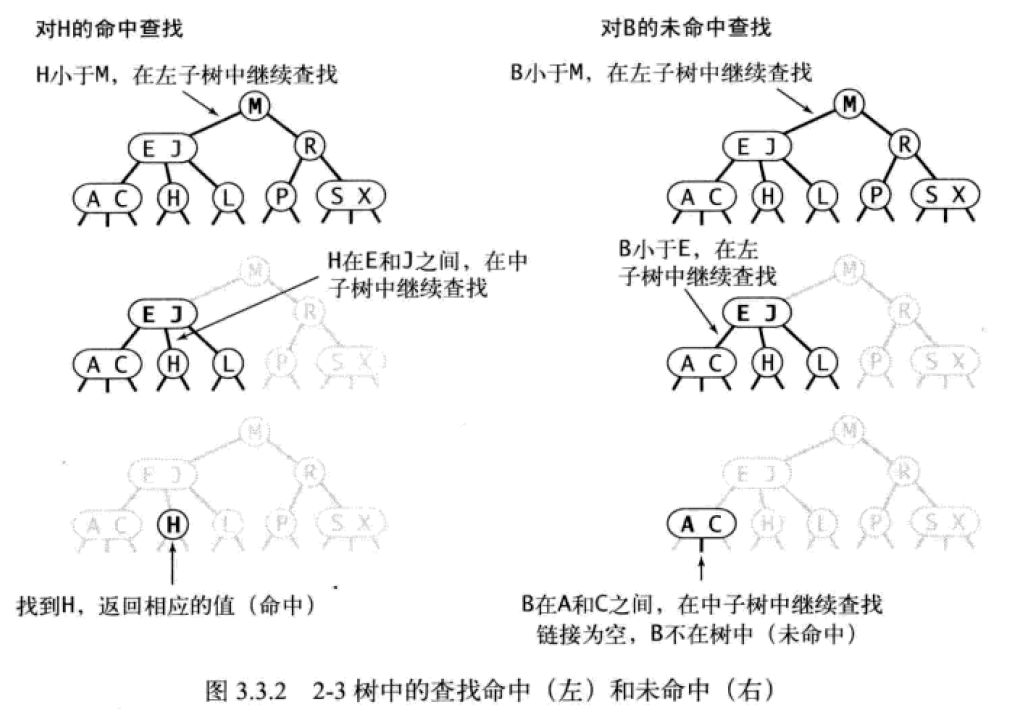
2-3 树的查找算法和二叉查找树算法类似：先从根节点比较，递归向下查找；如果相等则命中，否则根据比较结果指向相应的链接递归查找；如果是空链接表示查找未命中。

插入

2-3 树中的插入操作非常复杂，细分为如下几种情形：

向 2 节点中插入新键
向 3 节点中插入新键，整棵树只包含这个 3 节点
向 3 节点中插入新键，其父节点为 2 节点
向 3 节点中插入新键，其父节点为 3 节点

参考 2、3 节点的定义，引入 4 节点。所有 3 节点的插入操作，会涉及到 4 节点及对应转换。插入新键后，需要保持 2-3 查找树的平衡性、有序性，针对以上情形逐个分析：

向 2 节点中插入新键
查找到合适位置后，将新键直接加入 2 节点，使其成为一个 3 节点，完全不影响平衡性。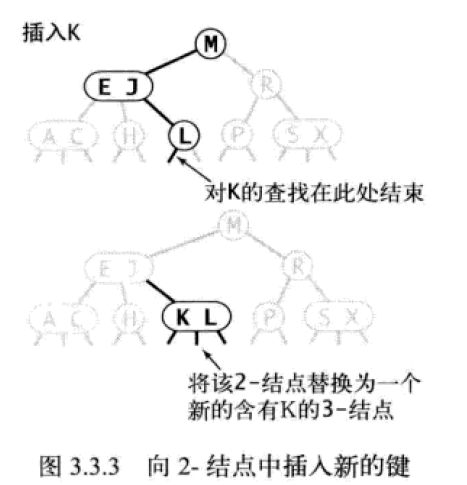
向 3 节点中插入新键，整棵树只包含这个 3 节点
先将新键存入 3 节点使其变为一个 4 节点，而 4 节点很容易分解为一颗由 3 个 2 节点组成的 2-3 树。此时这棵树既是一颗二叉查找树，同时也是一颗完美平衡的 2-3 树。这个场景插入新键前树高为 0，插入后高度增长为 1 。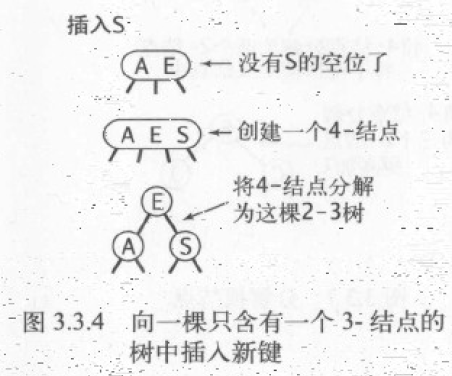
向 3 节点中插入新键，其父节点为 2 节点
先将新键存入 3 节点使其变为一个 4 节点，为了避免破坏平衡性，此时并不能直接将中键创建新节点，而是要将其移动到原来的父节点中。使父节点由 2 节点变为 3 节点。这次转换保持了树的平衡性和有序性。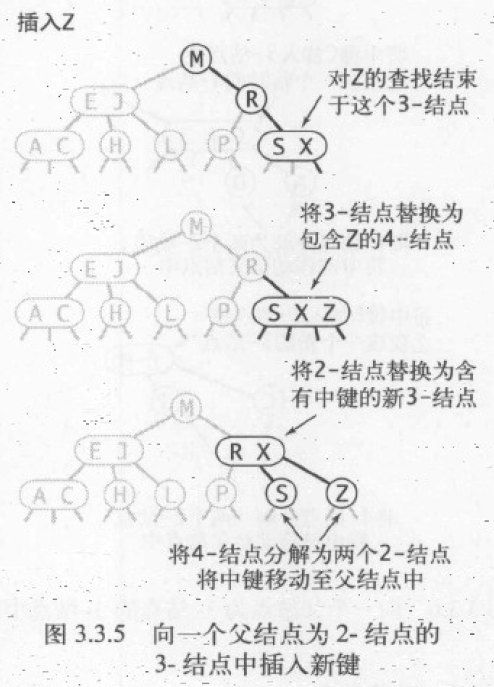
向 3 节点中插入新键，其父节点为 3 节点
先将新键存入 3 节点使其变为一个 4 节点，分解中键插入到父节点中，而父节点也是一个 3 节点。同理递归向上分解中键，直到不需要分解或者到达根节点。
如果递归分解中键到根节点，此时根节点是一个 4 节点，参考第二种情形，直接将该节点分解为 3 个 2 节点，使得树高加 1 。此时树仍然是平衡、有序的。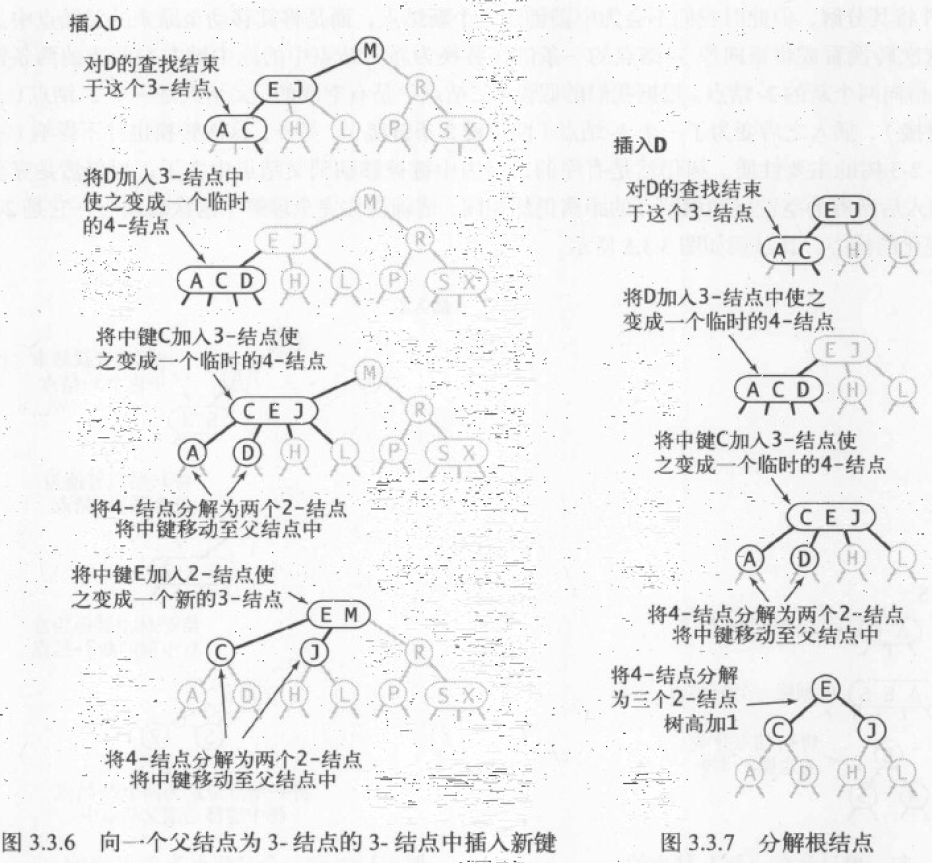

4 节点分解及其性质

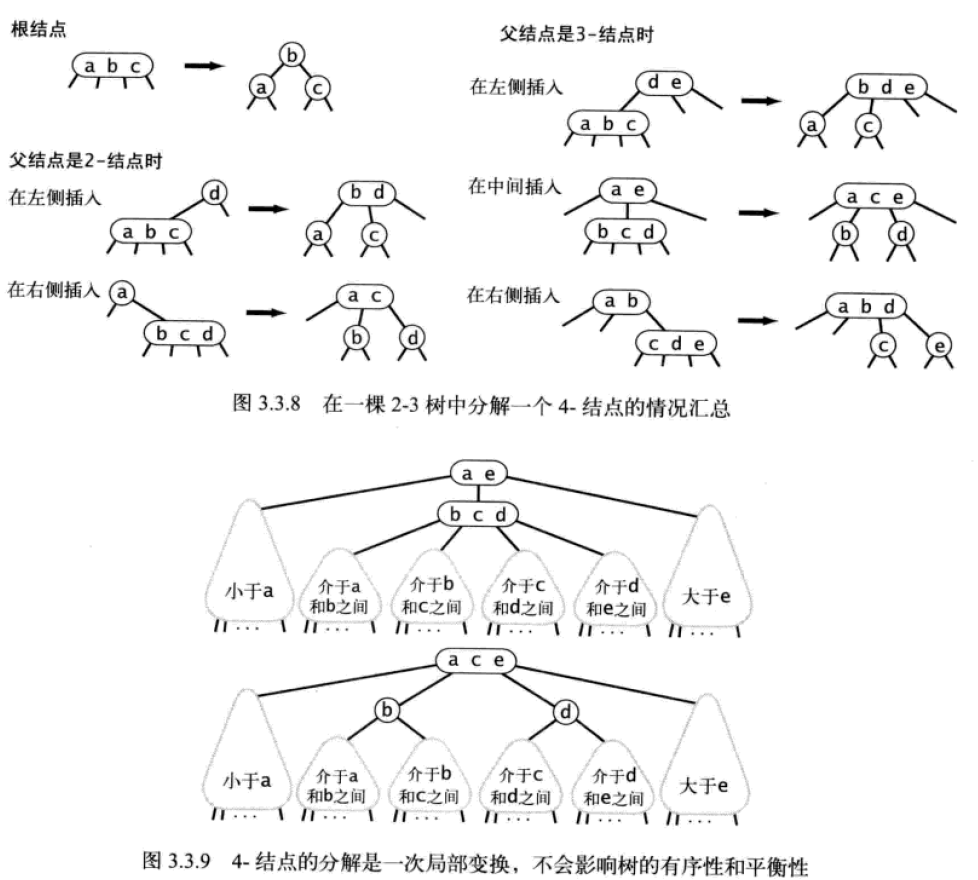
4 节点分解为 2-3 树一共包含 6 中情况。4 节点的分解变换都是局部的：除了相关的节点和链接之外不必修改或者检查树的其他部分。
这些局部变换也不会影响树的全局有序性和平衡性：任意空链接到根节点的路径长度都是相等的。

2-3 树构造

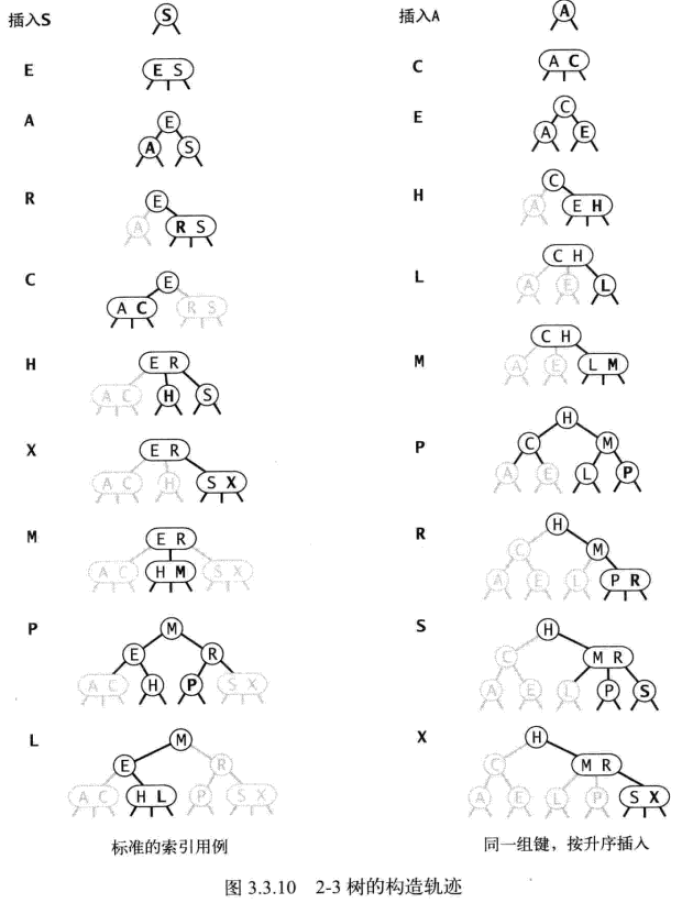
2-3 树构造过程是由下向上的，总是会经历 2 节点、 3 节点、 4 节点的转换。

小结

2-3 查找树中，插入和查找的时间复杂度必然不超过 logN，即使在最坏情况下，也能保持良好的平衡性
2-3 查找树因为涉及到多种节点，及类型转换，实现复杂

红黑树

定义

由于 2-3 树难于实现，所以使用一种名为红黑树的新数据结构来实现它。红黑树首先是一颗二叉查找树，它同时满足 5 条性质：

每个节点要么是红色要么就是黑色
根节点必须是黑色
每个空（NIL）节点必须是黑色
如果节点是红色，它的两个子节点必须是黑色
树是完美黑色平衡的：即任意空 NIL 节点到根节点路径上包含相同数量的黑色节点

红黑树实现有多种表达方式，但必须满足上面 5 条性质。红黑树目的是用标准的二叉查找树和红黑两种颜色来实现。《算法 4》中的实现有如下特点：

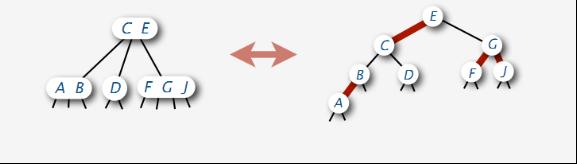
红链接：红色左链接连接的两个 2 节点，表示 2-3 树的 3 节点。其特点是：必须为左链接，且不能出现两条连续的红链接。
黑链接：表示 2-3 树中的 2 节点

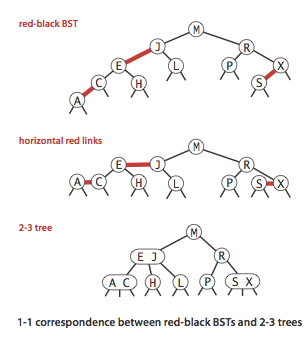
我们将红黑树中的红链接画平，那么所有空节点到根节点的距离都是相同的（黑色平衡），我们将红链接节点合并，即为一颗 2-3 树。相反，如果将 2-3 树的 3 节点画成由红色左链接相连的两个 2 节点，即转换为一颗红黑树。所以可以认为红黑树既是一颗二叉查找树，又是一颗 2-3 树。

红黑树节点比二叉查找树多了一个字段 color ，用来表示和其父节点链接的颜色。

private class Node {
    private Key key;           // key
    private Value val;         // associated data
    private Node left, right;  // links to left and right subtrees
    private boolean color;     // color of parent link
    private int size;          // subtree count

    public Node(Key key, Value val, boolean color, int size) {
        this.key = key;
        this.val = val;
        this.color = color;
        this.size = size;
    }
}

红黑树中红节点有多种表示方法，《算法 4》中采取的是 2-3 树表示法，也就是只有左红链接。而各种语言自带的 SDK 中红黑树通常是使用 2-3-4 树表示法，这种表示法中红节点可以是左链接、也可以是右链接。还有些算法论文中红黑树使用 2-3-4 树表示时，使用两个连续的左红链接来表示 4 节点。使用不同表示法，插入、删除、修复等算法实现会有较大差异。《算法 4 》使用的是 2-3 树，而《算法导论》则使用的是 2-3-4 树；不管使用哪种树，红黑树的 5 条基本性质不变。

旋转

以《算法 4》中，使用左红链接表示 3 节点，来解释红黑树的旋转。在插入或删除等操作后，可能会出现红色右链接或者两条连续的红链接，出现这些情况时需要旋转红链接并修复。

左旋转
红色右链接旋转为左链接。实现思路是将两个节点中，较大的作为根节点。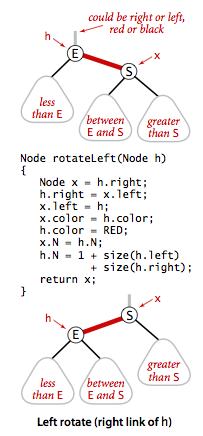
右旋转
红色左链接旋转为右链接。实现思路是将两个节点中，较小的作为根节点。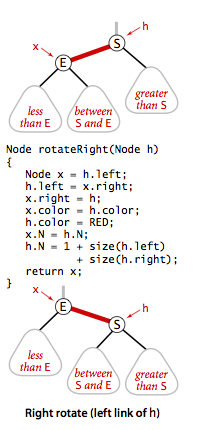

不管是左旋转还是右旋转，我们都不会改变其在父节点链接的颜色。这条链接可能是红色，也可能是黑色，总之旋转不会破坏节点和父节点链接的颜色。如果出现两条连续的红链接，需要递归旋转，直到根节点。

// 左旋转
// make a right-leaning link lean to the left
private Node rotateLeft(Node h) {
    // assert (h != null) && isRed(h.right);
    Node x = h.right;
    h.right = x.left;
    x.left = h;
    x.color = x.left.color;
    x.left.color = RED;
    x.size = h.size;
    h.size = size(h.left) + size(h.right) + 1;
    return x;
}

// 右旋转
private Node rotateRight(Node h) {
    // assert (h != null) && isRed(h.left);
    Node x = h.left;
    h.left = x.right;
    x.right = h;
    x.color = x.right.color;
    x.right.color = RED;
    x.size = h.size;
    h.size = size(h.left) + size(h.right) + 1;
    return x;
}

颜色转换

如果一个节点的两个子节点都为红色（可以理解为 2-3 树中的 4 节点），需要对这三个节点做颜色转换：两个子节点的颜色由红变黑，当前节点的颜色要由黑变红。相当于 4 节点的中键建立新键，插入到父节点中，使父节点变为 3 节点。
根节点：颜色旋转可能会将根节点变为红色，违背了红黑树的定义。因此每次插入节点时，都会将根节点设置为黑色。
颜色转换和旋转操作一样，都属于局部转换，不会破坏整棵树的黑色平衡性。

// flip the colors of a node and its two children
private void flipColors(Node h) {
    // h must have opposite color of its two children
    // assert (h != null) && (h.left != null) && (h.right != null);
    // assert (!isRed(h) &&  isRed(h.left) &&  isRed(h.right))
    //    || (isRed(h)  && !isRed(h.left) && !isRed(h.right));
    h.color = !h.color;
    h.left.color = !h.left.color;
    h.right.color = !h.right.color;
}

插入

《算法 4》的插入分析：2-3 树的插入复杂且情形很多，每次插入新键都会形成 3 节点或者 4 节点，需要逐一对应分析：

向 2 节点插入新键
插入新键时，总是用红链接将新节点和它的父节点相连（即产生一个 3 节点）。如果新节点是父节点的左链接，则直接形成 3 节点；如果新节点是父节点的右链接，形成的 3 节点颜色不对，需要左旋转修复。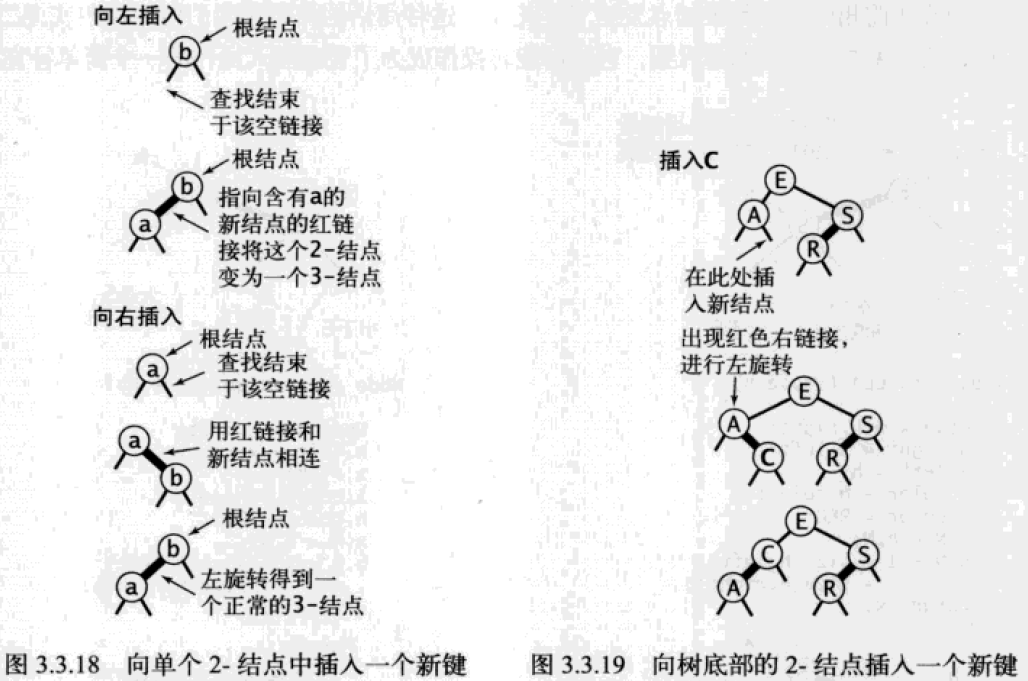
向 3 节点插入新键，整棵树只包含这个 3 节点
3 节点中插入新键时，会产生 4 节点，此时必然涉及到 4 节点的分解，即颜色转换。向 3 节点中插入新键时有三种情况：新键小于树中的两个键，在两个键之间，或者大于两个键。插入后会出现红色右链接、连续两个红链接、两个子节点都为红链接的情形，需要对应做左右旋转及颜色转换。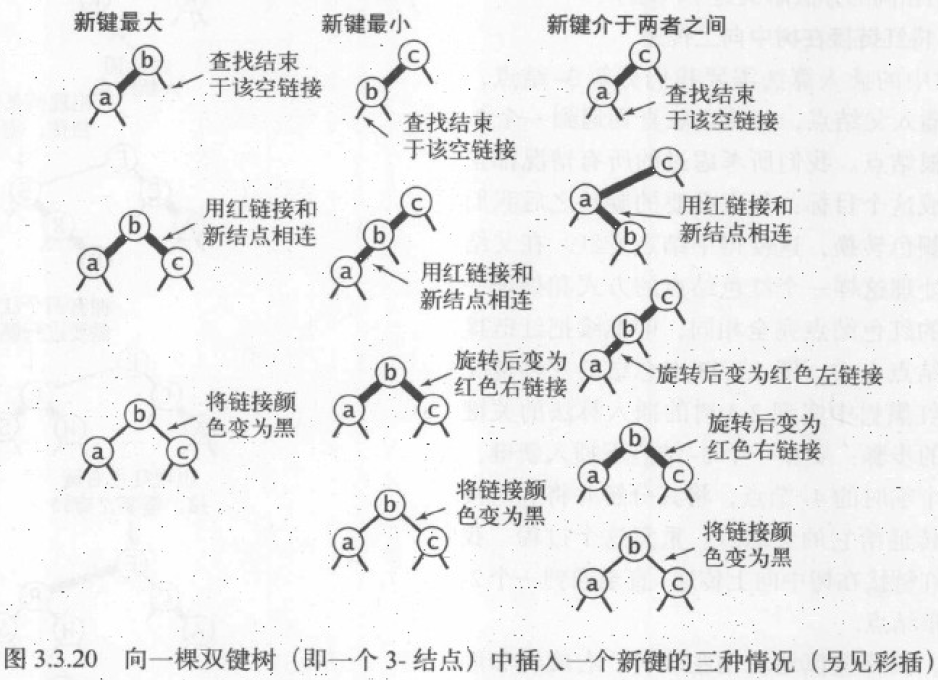
向 3 节点插入新键，3 节点位于树中或底部
操作方式和整个树为 3 节点类似，但是会使得红链接在树中向上传递。使用递归的方式处理这条红链接，直到遇到 2 节点或者根节点。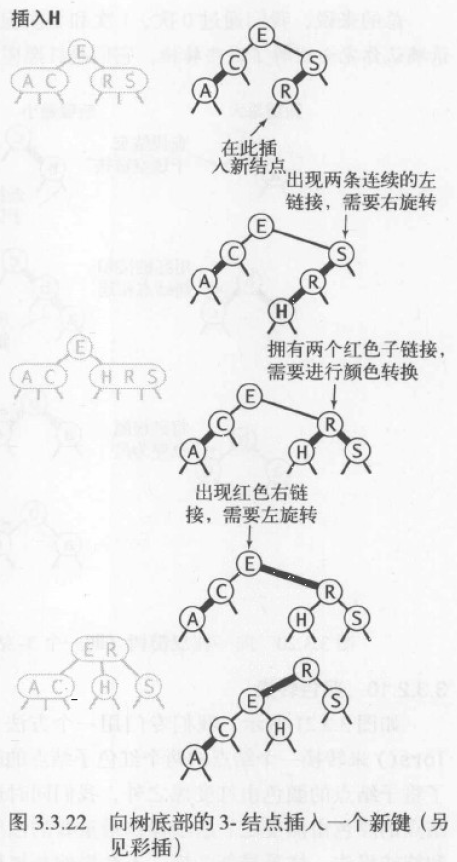

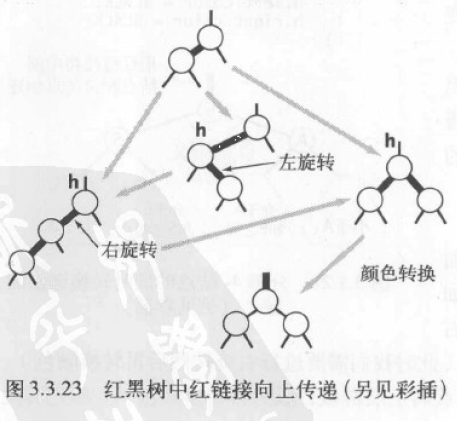
根据以上分析，插入新键小结如下：

新键节点总是红色
如果右子节点是红色而左子节点是黑色，则将该节点左旋转
如果左子节点是红色，且它的左子节点也是红色，即连续两条红链接，则将该节点右旋转
如果左右两个子节点都是红色，进行颜色转换
不管是那种情形的插入，插入新节点后，必须将根节点置为黑色

public void put(Key key, Value val) {
    if (key == null) throw new IllegalArgumentException("key is null");
    if (val == null) {
        delete(key);
        return;
    }

    root = put(root, key, val);
    // 每次插入新键，必须将根节点设置为黑色
    root.color = BLACK;
    // assert check();
}

// insert the key-value pair in the subtree rooted at h
private Node put(Node h, Key key, Value val) { 
    // 如果没有找到，新键一个节点
    // 新键默认为红色，即新插入节点会形成 3 节点或 4 节点
    if (h == null) return new Node(key, val, RED, 1);

    // 递归查找，新键插入到左子树还是右子树
    int cmp = key.compareTo(h.key);
    if      (cmp < 0) h.left  = put(h.left,  key, val); 
    else if (cmp > 0) h.right = put(h.right, key, val); 
    else              h.val   = val;

    // fix-up any right-leaning links
    // 如果右子节点是红色而左子节点是黑色，则将该节点左旋转
    if (isRed(h.right) && !isRed(h.left))      h = rotateLeft(h);
    // 如果左子节点是红色，且它的左子节点也是红色
    // 即连续两条红链接，则将该节点右旋转
    if (isRed(h.left)  &&  isRed(h.left.left)) h = rotateRight(h);
    // 如果左右两个子节点都是红色，进行颜色转换  
    if (isRed(h.left)  &&  isRed(h.right))     flipColors(h);
    
    // 递归更新节点数
    h.size = size(h.left) + size(h.right) + 1;

    return h;
}

构造轨迹

根据上面插入新键的思路，得到的红黑树是一颗接近完美平衡的二叉查找树。如下示例为同一组键值对，按照不同顺序构建的红黑树。

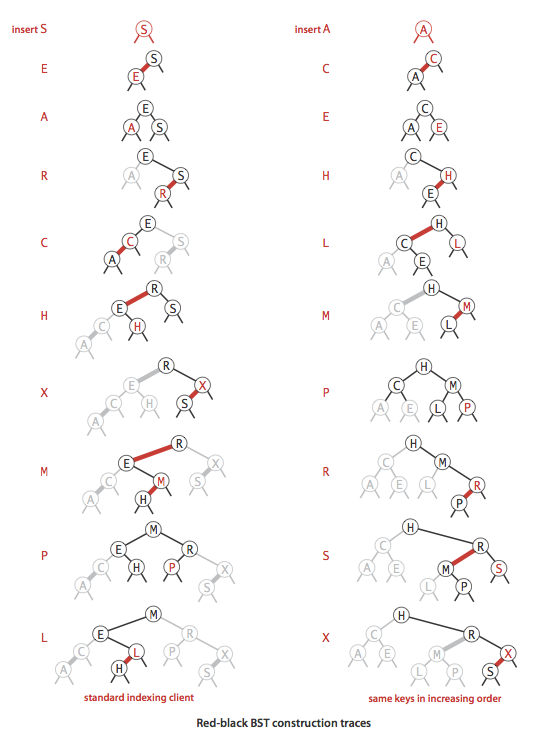
查找

红黑树的查找算法和二叉查找树算法完全一致。

public Value get(Key key) {
    if (key == null) throw new IllegalArgumentException("argument is null");
    return get(root, key);
}

// value associated with the given key in subtree rooted at x; 
// null if no such key
private Value get(Node x, Key key) {
    while (x != null) {
        int cmp = key.compareTo(x.key);
        if      (cmp < 0) x = x.left;
        else if (cmp > 0) x = x.right;
        else              return x.val;
    }
    return null;
}

删除及有序性

《算法 4》中并没有详细分析红黑树的删除，删除这个过程非常复杂，本文在 TreeMap 源码分析中详细介绍删除过程。

`JDK` 中的红黑树 `TreeMap`

java.util.TreeMap.java 是 JDK 中红黑树的实现，并且 java.util.HashMap.java 使用拉链法解决冲突时，链表个数超过 8 个会自动转换为红黑树。

节点

TreeMap 是使用 2-3-4 树的思路来实现红黑树的，参考了《算法导论》的伪代码来实现。如下示例将红节点“拉平”后，为一颗完美平衡的 2-3-4 树。

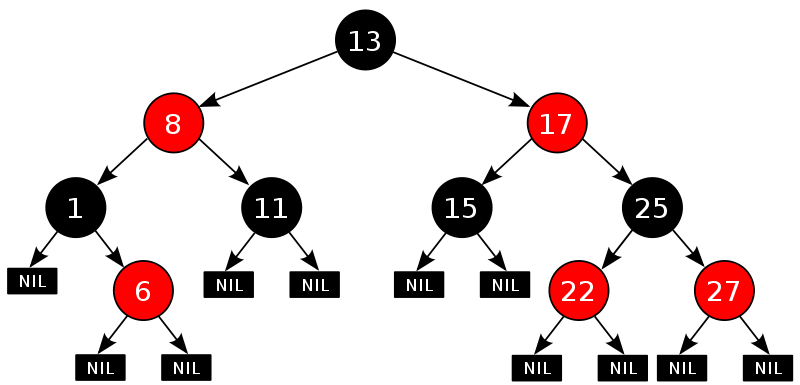
新建节点默认为黑色（但是插入修复时，总是会先将新节点设置为红色），节点中有三条链接分别指向：左子树、右子树、父节点。

private static final boolean RED   = false;
private static final boolean BLACK = true;
static final class Entry<K,V> implements Map.Entry<K,V> {
    K key;
    V value;
    Entry<K,V> left;
    Entry<K,V> right;
    Entry<K,V> parent;
    // 默认为黑色节点
    boolean color = BLACK;

    Entry(K key, V value, Entry<K,V> parent) {
        this.key = key;
        this.value = value;
        this.parent = parent;
    }

    public K getKey() {return key;}
    public V getValue() {return value;}
    public V setValue(V value) {...}
    public boolean equals(Object o) {...}
    public int hashCode() {...}
    public String toString() {...}
}

旋转

2-3 树和 2-3-4 树旋转的概念是一样的，都是红色节点的左右旋。

private void rotateLeft(Entry<K,V> p) {
    if (p != null) {
        Entry<K,V> r = p.right;
        p.right = r.left;
        if (r.left != null)
            r.left.parent = p;
        r.parent = p.parent;
        if (p.parent == null)
            root = r;
        else if (p.parent.left == p)
            p.parent.left = r;
        else
            p.parent.right = r;
        r.left = p;
        p.parent = r;
    }
}

private void rotateRight(Entry<K,V> p) {
    if (p != null) {
        Entry<K,V> l = p.left;
        p.left = l.right;
        if (l.right != null) l.right.parent = p;
        l.parent = p.parent;
        if (p.parent == null)
            root = l;
        else if (p.parent.right == p)
            p.parent.right = l;
        else p.parent.left = l;
        l.right = p;
        p.parent = l;
    }
}

前驱和后继

前驱：小于当前节点的最大节点
后继：大于当前节点的最小节点

换句话说，在红黑树排序中，前驱为当前节点的前一个，后继为当前节点的后一个。如下为后继节点图示：

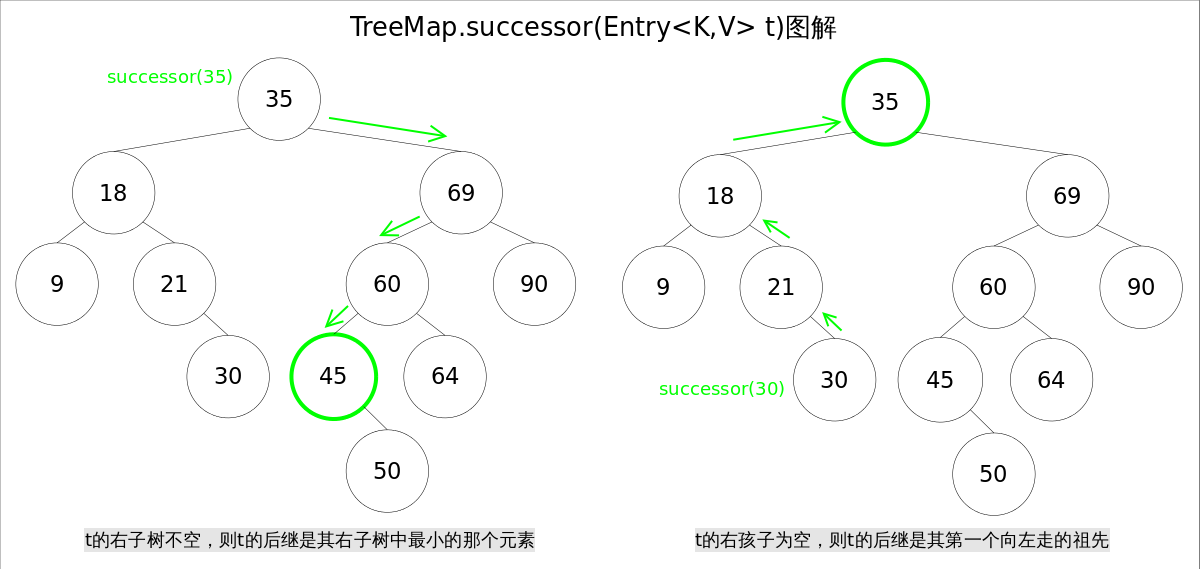
在看红黑树的文章时，网上经常出现一个结论：前驱或者后继节点最多包含一个子节点。这个结论并不准确！比如：当前节点为叶子节点或者只包含一个子节点时，则其前驱或者后继最多能包含两个节点。
示例：当前节点为叶子节点 30 ，其前驱为 21 包含一个子节点，后继为 35 包含两个子节点；当前节点为 45 ，只包含一个子节点，其前驱为 35 包含两个子节点，后继为 50 不包含子节点。
所以这个结论需要有一个前提条件才是正确的：当前节点有两个子节点时，其前驱或者后继最多只有一个子节点。

/**
 * Returns the successor of the specified Entry, or null if no such.
 */
static <K,V> TreeMap.Entry<K,V> successor(Entry<K,V> t) {
    if (t == null)
        return null;
    // t 的右子树不空，则 t 的后继是其右子树中最小的那个元素
    else if (t.right != null) {
        Entry<K,V> p = t.right;
        while (p.left != null)
            p = p.left;
        return p;
    } else {
    // t 的右子树为空，则 t 的后继是其第一个向左走的祖先
        Entry<K,V> p = t.parent;
        Entry<K,V> ch = t;
        while (p != null && ch == p.right) {
            ch = p;
            p = p.parent;
        }
        return p;
    }
}

/**
 * Returns the predecessor of the specified Entry, or null if no such.
 */
static <K,V> Entry<K,V> predecessor(Entry<K,V> t) {
    if (t == null)
        return null;
    else if (t.left != null) {
        Entry<K,V> p = t.left;
        while (p.right != null)
            p = p.right;
        return p;
    } else {
        Entry<K,V> p = t.parent;
        Entry<K,V> ch = t;
        while (p != null && ch == p.left) {
            ch = p;
            p = p.parent;
        }
        return p;
    }
}

插入

先循环查找新键插入的合适位置，插入后修复整棵树的平衡性。哪些节点需要修复？同时满足下面两条：

当前节点为红节点（修复时，新插入的节点总是设置为红色，也就是实际上新建节点默认是红色）
当前节点的父节点也为红节点

也就是说：如果出现上下连续两个红节点，则需要修复。修复分为三种情况：

叔叔结点（祖父结点的另一个子结点）是红色
修复方案：颜色转换，红色上移！父节点和叔叔节点变黑，祖父节点变为红色。祖父节点作为当前节点循环修复！
颜色：父节点和叔叔节点变黑，祖父节点变为红色。
旋转：不做旋转。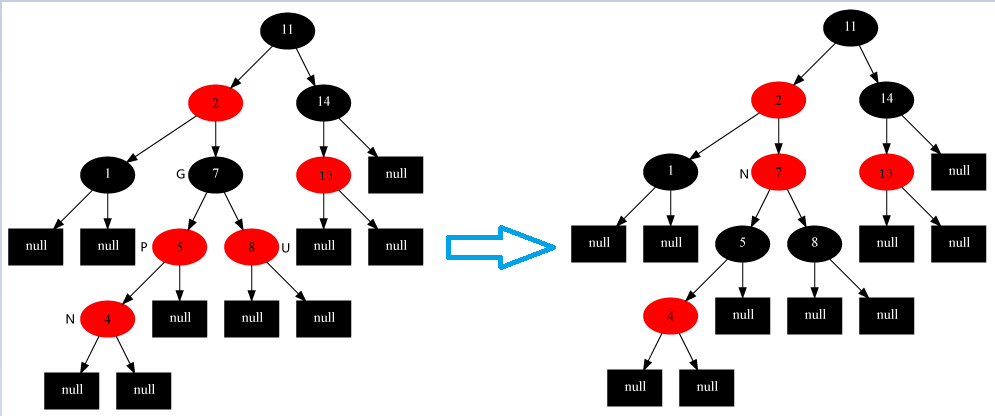
叔叔节点是黑色，当前结点是其父结点的右子
修复方案：父节点作为当前节点左旋。
颜色：不改变颜色。
旋转：父节点变成兄弟节点。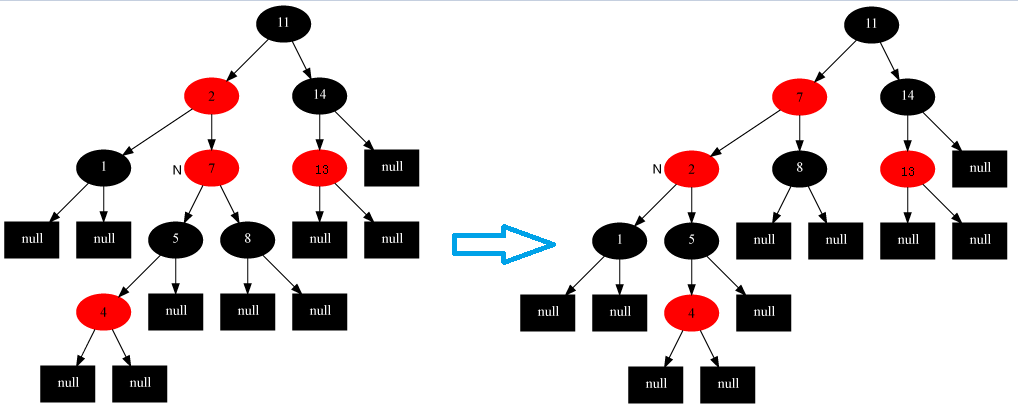
叔叔节点是黑色，当前结点是其父结点的左子
也就是：当前节点，父节点，祖父节点同为左边一条线或者右边一条线
修复方案：父节点变为黑色，祖父节点变为红色，并且祖父节点右旋。
颜色：父节点变为黑色，祖父节点变为红色。
旋转：祖父节点变为叔叔节点。

图示中：N 表示新建节点或当前节点；P 表示父节点；G 表示祖父节点。

小结：

插入修复，主要参考的是父节点和叔叔节点的颜色
情形一祖父节点循环修复；情形二和情形三顺序执行后退出
修复的最后一步是确保根节点为黑色
上面三种情况都会有对称情形，请看下面代码。也就说实际上是有 6 中情形，因为对称只需要分析三种情形
修复所做的旋转不会超过 2 次

如下为红黑树插入动态图，动图生成网址，插入顺序为 12, 1, 9, 2, 0, 11, 7, 19, 4, 15, 18, 5, 14, 13, 10, 16, 6, 3, 8, 17 ：

// 循环遍历找到新键插入的合适位置
public V put(K key, V value) {
    Entry<K,V> t = root;
    if (t == null) {
        compare(key, key); // type (and possibly null) check

        root = new Entry<>(key, value, null);
        size = 1;
        modCount++;
        return null;
    }
    int cmp;
    Entry<K,V> parent;
    // split comparator and comparable paths
    // 指定比较器
    Comparator<? super K> cpr = comparator;
    if (cpr != null) {
        do {
            parent = t;
            cmp = cpr.compare(key, t.key);
            if (cmp < 0)
                t = t.left;
            else if (cmp > 0)
                t = t.right;
            else
                return t.setValue(value);
        } while (t != null);
    }
    // 没有指定比较器，直接比较
    else {...}
    Entry<K,V> e = new Entry<>(key, value, parent);
    if (cmp < 0)
        parent.left = e;
    else
        parent.right = e;
    fixAfterInsertion(e);
    size++;
    modCount++;
    return null;
}

// 插入后修复新键及整颗树的平衡性
private void fixAfterInsertion(Entry<K,V> x) {
    // 修复的条件：上下连续两个红节点
    x.color = RED;

    while (x != null && x != root && x.parent.color == RED) {
        // 父节点为左子树
        if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
            // 获取叔叔节点
            Entry<K,V> y = rightOf(parentOf(parentOf(x)));
            // 情形 1：叔叔节点为红色
            if (colorOf(y) == RED) {
                // 修复方案：颜色转换，红色上移！
                // 父节点和叔叔节点变黑，祖父节点变为红色
                // 祖父节点作为当前节点循环修复
                setColor(parentOf(x), BLACK);
                setColor(y, BLACK);
                setColor(parentOf(parentOf(x)), RED);
                x = parentOf(parentOf(x));
            } else {
                // 情形 2：叔叔节点是黑色，当前结点是其父结点的右子
                // 修复方案：父节点作为当前节点左旋
                if (x == rightOf(parentOf(x))) {
                    x = parentOf(x);
                    rotateLeft(x);
                }
                // 当前节点左旋后，自动进入情形 3 （满足左子条件）
                // 情形 3：叔叔节点是黑色，当前结点是其父结点的左子
                // 修复方案：父节点变为黑色，祖父节点变为红色，并且祖父节点右旋
                setColor(parentOf(x), BLACK);
                setColor(parentOf(parentOf(x)), RED);
                rotateRight(parentOf(parentOf(x)));
            }
        } else {
        // 父节点为右子树，获取叔叔节点
            Entry<K,V> y = leftOf(parentOf(parentOf(x)));
            if (colorOf(y) == RED) {
                setColor(parentOf(x), BLACK);
                setColor(y, BLACK);
                setColor(parentOf(parentOf(x)), RED);
                x = parentOf(parentOf(x));
            } else {
                if (x == leftOf(parentOf(x))) {
                    x = parentOf(x);
                    rotateRight(x);
                }
                setColor(parentOf(x), BLACK);
                setColor(parentOf(parentOf(x)), RED);
                rotateLeft(parentOf(parentOf(x)));
            }
        }
    }
    
    // 修复完后，根节点必须设置为黑色
    root.color = BLACK;
}

删除节点

大致思路：找到被删节点 –> 找到替换节点 –> 删除或者修复

找被删节点：如果被删节点有两个子节点，复制后继节点（或者前驱）到被删节点（仅拷贝键值对，被删节点的三条链接和颜色保持不变），并使用其后继节点（或者前驱）作为新的被删节点
找替换节点：如果被删节点左子节点不为空，则用左子节点作为替换节点；否则用右子节点作为替换节点

如果替换节点不为空，则先删除再修复替换节点；如果替换节点为空（即被删节点为叶子节点），则先修复被删节点，再删除被删节点：

删除：被删除节点的左右父三条链接都置空，使用替换节点替换到被删节点的位置。除了修改替换节点的父链接，替换节点的颜色等其他信息全部保留
修复：被修复节点如果是黑色且不为根节点，需要变色和旋转；否则直接将被修复节点置黑结束修复。修复节点可能是替换节点（删除节点和替换节点都为黑色时，即连续两个黑色节点），也可能是被删节点（被删节点为黑色叶子节点，即黑叶子）。

被删节点的特点：

被删节点最多只包含一个子节点
分析如下：因为是二叉查找树，所以被删节点可能为叶子节点、只包含一个子节点、有两个子节点。而当被删节点有两个子节点时，需要使用前驱或者后继复制到被删节点位置，并将前驱或者后继作为新的被删节点。而被删节点有两个子节点时，其前驱或者后继（在其左右子树中）必定最多只会包含一个子节点。替换节点则为这个唯一的子节点或者为空节点。
被删节点为黑色才进入修复
如果被删节点是红色（表示是 3 节点或 4 节点），则直接删除该节点，并用替换节点替换后结束。如果被删节点是黑色（表示是 2 节点），删除后会导致左右不平衡，则进入修复流程。被修复节点可能是被删节点或者替换节点。

被修复节点的特点：

可能是被删节点或替换节点
颜色可红可黑：如果是被删节点必为黑色；如果是替换节点，可红可黑

修复节点

节点的假设：
被删除的节点为 X，其替换节点（孩子节点）为 N，大部分学习资料上，在讲删除后修复时，都是将 X 节点省略掉了，直接使用 N 节点替代了 X 节点的位置。不管是修复被删节点还是修复替换节点，本文使用 R 表示被修复节点。
而修复时，被修复节点 R 的父节点为 P，兄弟节点为 S；S 的左子节点为 SL，右子节点为 SR。

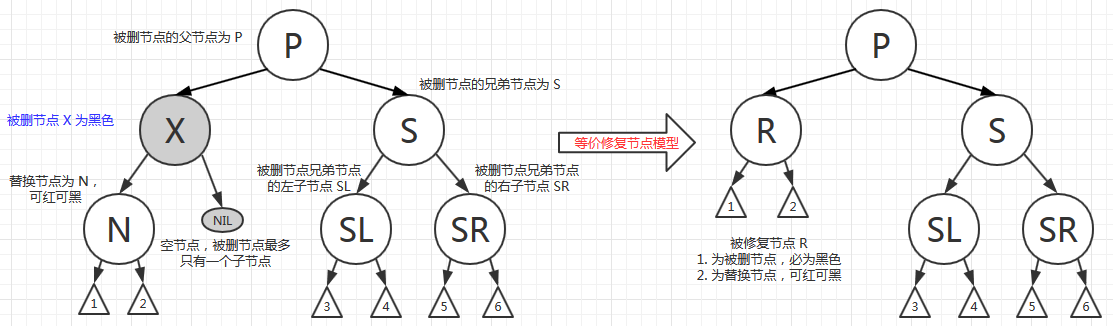
修复中需要变色和旋转的四种情形细分，图示中白色表示任意颜色，黑色表示黑节点，红色表示红节点：

情形一：兄弟节点是红色的
修复方案：父节点和兄弟节点颜色互换，父节点旋转。
颜色：父节点变为红色，兄弟节点变为黑色。
旋转：向左或者向右旋转父节点，将兄弟节点旋转成祖父节点。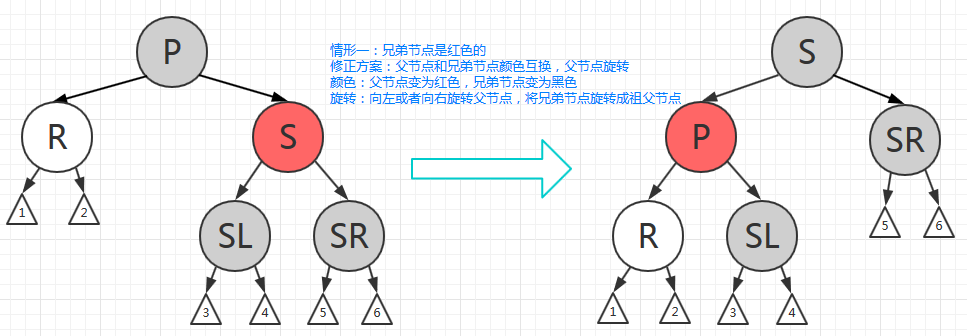
情形二：兄弟节点是黑色的，而且其两个子节点也是黑色的
修复方案：兄弟节点设置为红色，并将父节点作为被修复节点从情形一开始循环修复。
颜色：仅改变兄弟节点颜色，设置为红色。
旋转：不做任何旋转。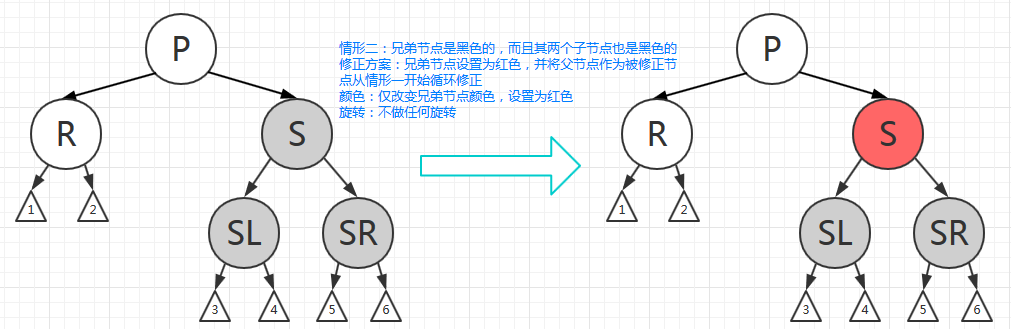
情形三：兄弟节点是黑色的，其左子节点是红色的，右子节点是黑色的
修复方案：兄弟节点和兄左子节点颜色互换，兄弟节点右旋。
颜色：兄弟节点变为红色，兄弟子节点由红变黑。
旋转：向右旋转兄弟节点，也就是将兄子节点旋转成兄弟节点。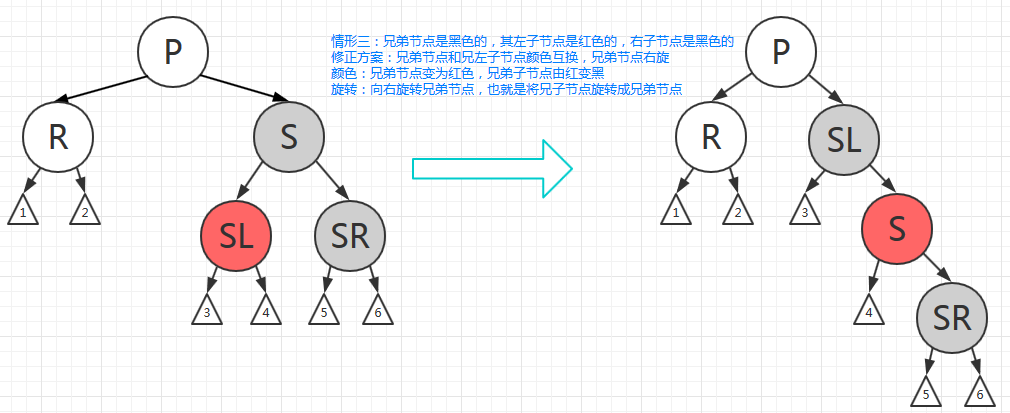
情形四：兄弟节点是黑色的，其右子节点是红色的
修复方案：兄弟节点的右子节点设置为黑色，兄弟节点和父节点颜色互换，父节点左旋。
颜色：兄子节点由红变黑，父节点不管是什么颜色都和兄弟节点颜色互换，父节点变成黑色。
旋转：父节点旋转，也就是将兄弟节点旋转成父节点。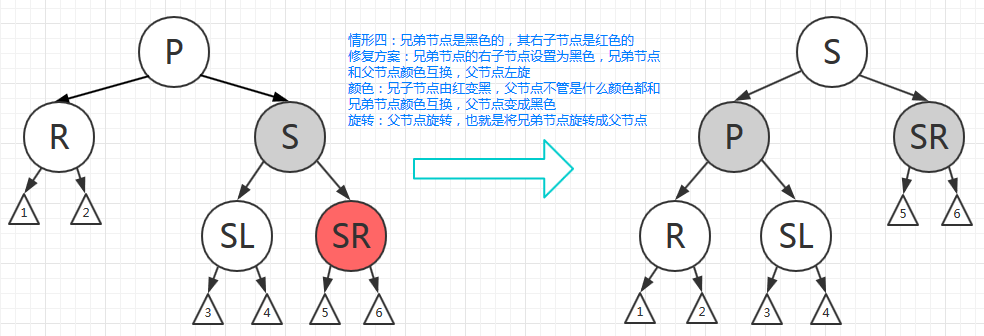

小结：

不管修复前节点是什么颜色，修复完后必须将被修复节点设置为黑色
上面四种情形顺序执行，只有情形二结束时从父节点开始重新循环修复，情形四结束时退出循环
上面的左右旋转、兄弟左右子节点颜色，因为存在对称关系，所以实际存在 8 种情形
修复所做的旋转不会超过 3 次

如下为红黑树删除动态图，动图生成网址，删除顺序为 12, 1, 9, 2, 0, 11, 7, 19, 4, 15, 18, 5, 14, 13, 10, 16, 6, 3, 8, 17，删除后使用前驱作为替换节点：

删除和修复源码

private void deleteEntry(Entry<K,V> p) {
    // 1. 找被删节点：p 为被删节点
    modCount++;
    size--;

    // If strictly internal, copy successor's element to p and then make p
    // point to successor.
    // 如果被删节点的两个子节点不为空
    if (p.left != null && p.right != null) {
        // 找到后继节点，并将键值对复制给被删节点
        Entry<K,V> s = successor(p);
        p.key = s.key;
        p.value = s.value;
        // 被删节点指向后继节点；即后继节点作为新的被删节点
        p = s;
    } // p has 2 children

    // Start fixup at replacement node, if it exists.
    // 2. 找替换节点：替换节点为被删节点子节点
    // 默认左子节点，如果左子节点为空，则替换节点为右子节点
    Entry<K,V> replacement = (p.left != null ? p.left : p.right);

    if (replacement != null) {
        // 替换节点不为空，先删除再修复
        // Link replacement to parent
        // 替换节点替换被删节点
        replacement.parent = p.parent;
        // 父节点为根节点
        if (p.parent == null)
            root = replacement;
        // 父节点为左节点
        else if (p == p.parent.left)
            p.parent.left  = replacement;
        // 父节点为右节点
        else
            p.parent.right = replacement;

        // Null out links so they are OK to use by fixAfterDeletion.
        // 被删节点三条链接置空
        p.left = p.right = p.parent = null;

        // Fix replacement
        if (p.color == BLACK)
            fixAfterDeletion(replacement);
    } else if (p.parent == null) { // return if we are the only node.
        root = null;
    } else { //  No children. Use self as phantom replacement and unlink.
        // 替换节点为空，则先修复再删除
        if (p.color == BLACK)
            fixAfterDeletion(p);

        if (p.parent != null) {
            if (p == p.parent.left)
                p.parent.left = null;
            else if (p == p.parent.right)
                p.parent.right = null;
            p.parent = null;
        }
    }
}

/** From CLR */
private void fixAfterDeletion(Entry<K,V> x) {
    // 被修复节点不为根节点并且为黑色时，才需要修复
    while (x != root && colorOf(x) == BLACK) {
        if (x == leftOf(parentOf(x))) {
            // 兄弟节点
            Entry<K,V> sib = rightOf(parentOf(x));

            // 情形一：兄弟节点是红色的
            if (colorOf(sib) == RED) {
                setColor(sib, BLACK);
                setColor(parentOf(x), RED);
                rotateLeft(parentOf(x));
                sib = rightOf(parentOf(x));
            }

            // 情形二：兄弟节点是黑色的，而且其两个子节点也是黑色的
            if (colorOf(leftOf(sib))  == BLACK &&
                colorOf(rightOf(sib)) == BLACK) {
                setColor(sib, RED);
                x = parentOf(x);
            } else {
                // 情形三：兄弟节点是黑色的，其左子节点是红色的，右子节点是黑色的
                if (colorOf(rightOf(sib)) == BLACK) {
                    setColor(leftOf(sib), BLACK);
                    setColor(sib, RED);
                    rotateRight(sib);
                    sib = rightOf(parentOf(x));
                }
                // 情形四：兄弟节点是黑色的，其右子节点是红色的
                setColor(sib, colorOf(parentOf(x)));
                setColor(parentOf(x), BLACK);
                setColor(rightOf(sib), BLACK);
                rotateLeft(parentOf(x));
                x = root;
            }
        } else { // symmetric
            Entry<K,V> sib = leftOf(parentOf(x));

            if (colorOf(sib) == RED) {
                setColor(sib, BLACK);
                setColor(parentOf(x), RED);
                rotateRight(parentOf(x));
                sib = leftOf(parentOf(x));
            }

            if (colorOf(rightOf(sib)) == BLACK &&
                colorOf(leftOf(sib)) == BLACK) {
                setColor(sib, RED);
                x = parentOf(x);
            } else {
                if (colorOf(leftOf(sib)) == BLACK) {
                    setColor(rightOf(sib), BLACK);
                    setColor(sib, RED);
                    rotateLeft(sib);
                    sib = leftOf(parentOf(x));
                }
                setColor(sib, colorOf(parentOf(x)));
                setColor(parentOf(x), BLACK);
                setColor(leftOf(sib), BLACK);
                rotateRight(parentOf(x));
                x = root;
            }
        }
    }

    // 被修复节点最终都会被置为黑色
    setColor(x, BLACK);
}

小结

红黑树的插入、删除等算法都比较复杂，但是其带有的优点足以学习并使用它：

红黑树是接近完美平衡的二叉查找树
红黑树的查找，插入，删除等操作，最坏情况下的时间复杂度都能达到 O(logN)

其他

v_JULY_v: 红黑树插入删除全图解这篇文章在“删除”图示中，删除 12，1 两个节点使用的是前驱作为替换节点，而其他节点使用后继作为替换节点
红黑树的删除依然是使用 case N 大法来分析的，很容易忘记。后期需要找到一种更好的理解方式来学习删除

参考文档

《算法：第四版》第 3 章
《算法导论》第 13 章：红黑树
红黑树动画演示
wiki 红黑树
Left-Leaning Red-Black Trees, Dagstuhl Workshop on Data Structures, Wadern, Germany, February, 2008.
v_JULY_v: 彻底明白红黑树
v_JULY_v: 教你透彻了解红黑树
v_JULY_v: 红黑树插入删除全图解
平衡查找树之红黑树
CLR: Introduction to Algorithms 算法导论
红黑树画图工具
红黑树详细分析
TreeMap 源码分析
从2-3-4树到红黑树
通过2-3-4树理解红黑树
史上最清晰的红黑树讲解