算法 - 拓扑排序

发表于 | 分类于 | 阅读次数

拓扑排序：针对有向无环图来排序。

概念

定义

对一个有向无环图 DAG: Directed Acyclic Graph 进行拓扑排序，是将图 G 中所有顶点排成一个线性序列，使得图中任意一对顶点 u 和 v，若边 (u,v)∈E(G)，则 u 在线性序列中出现在 v 之前。通常这样的线性序列称为满足 拓扑次序 Topological Order 的序列，简称拓扑序列。
简单的说，由某个集合上的一个偏序得到该集合上的一个全序，这个操作称之为拓扑排序。当且仅当一幅图为有向无环图时才能进行拓扑排序。

AOV 网

有向图中若以顶点表示活动，有向边表示活动之间的先后关系，这样的图简称为 AOV 网 Activity On Vertex Network 。如下图是计算机专业课程之间的先后关系：

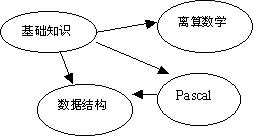
0092-topological-sorting-aov.jpg

AOV 网：是一个有向无环图，通常用来表示：

  • 课程先后关系
    哪个课程必须先修，修某个课程前必须修完哪些指定课程等。
  • 工程先后关系
    哪些子工程必须先做完，做某个工程前必须将哪些工程先做完。

所以 AOV 网在实际中非常实用，可以通过拓扑排序来找出这些活动的先后关系序列。

排序思路

拓扑排序在 AOV 网中排序方法如下：

  • 在网中选择一个入度为 0（没有前驱）的顶点输出
  • 在网中删除该顶点及与该顶点有关的所有边
  • 重复上述两步，直到网中不存在入度为 0 的顶点

如果所有顶点输出则拓扑排序完成，否则表示网中存在回路。
从上面算法思路中可以看出，拓扑排序和选择顶点的顺序有很大关系，所以拓扑排序输出顺序不是唯一的。

深度优先搜索递归实现

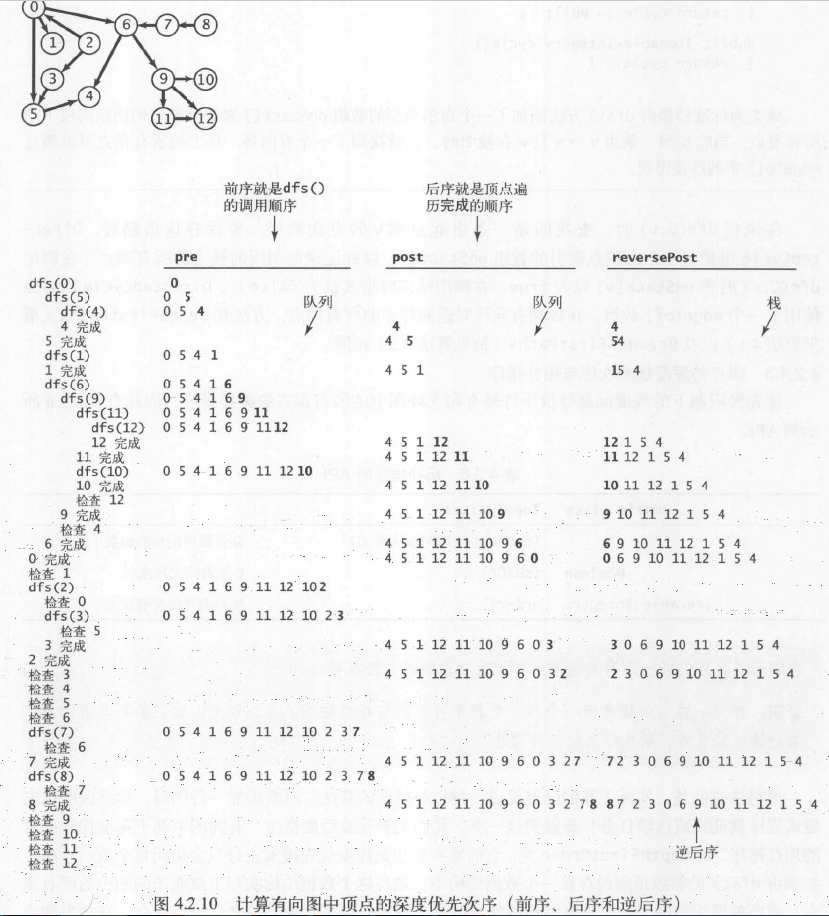
前序/后序/逆后序

深度优先搜索在遍历图的过程中，可以记录如下顺序：

  • 前序
    即在递归调用之前将顶点加入队列；意义：代表深度优先搜索访问顶点的顺序。
  • 后序
    即在递归调用之后将顶点加入队列；意义：代表深度优先搜索顶点遍历完成的顺序。
  • 逆后序
    即在递归调用之后将顶点压入栈；意义：代表着顶点的拓扑排序。

一幅有向无环图的拓扑排序即为所有顶点的逆后序排列。

0092-topological-sorting-dfs-preorder-postorder-reversepost.png

动图演示

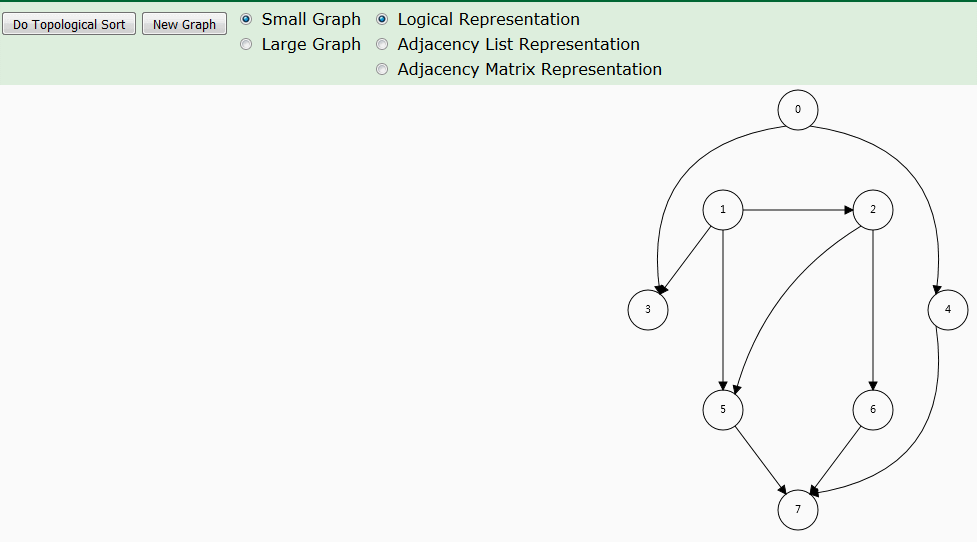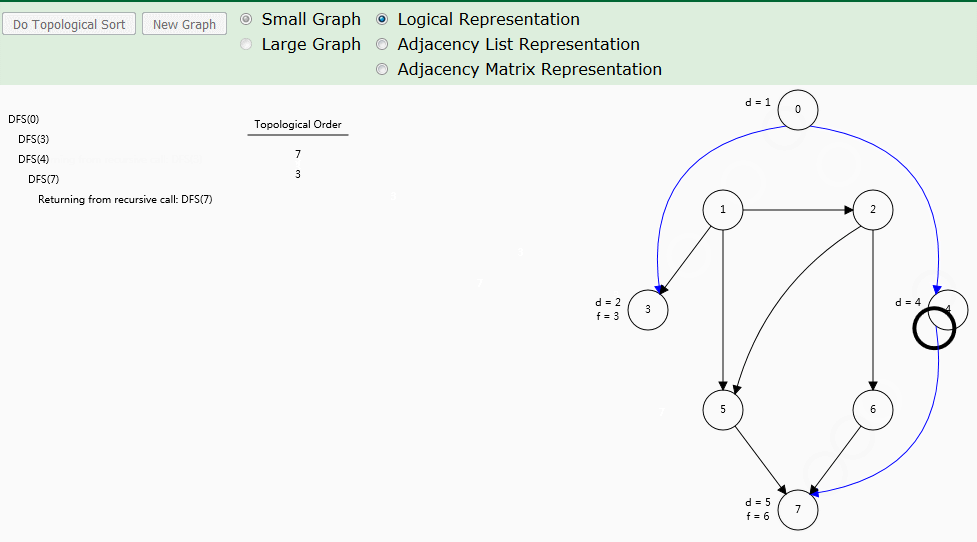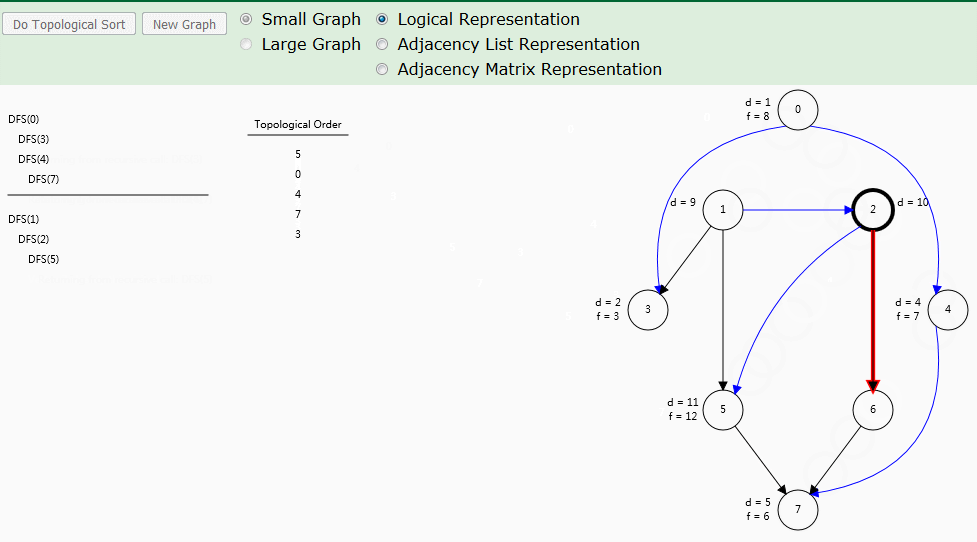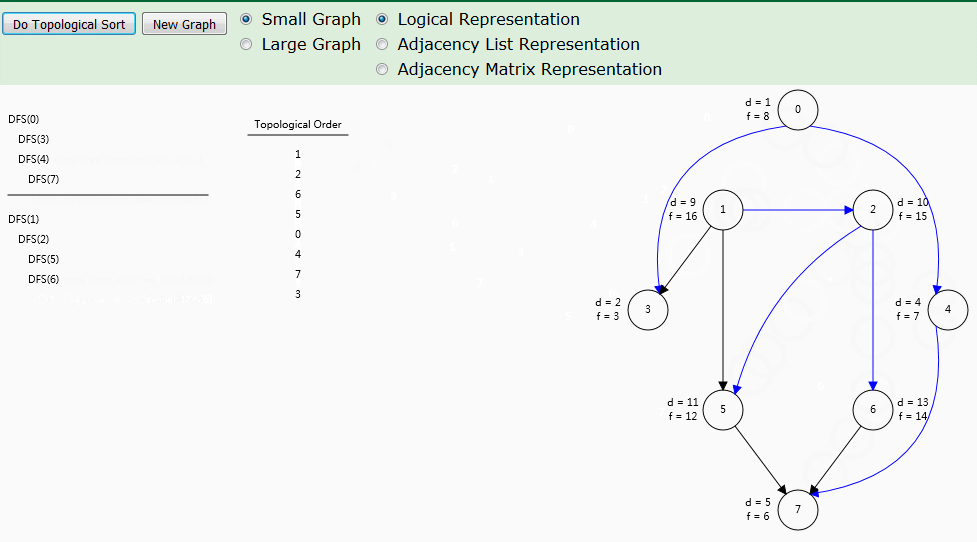
0092-topological-sorting-dfs.gif

算法解析

  • marked 数组
    记录当前顶点是否被访问过。
  • onStack 数组
    记录同一次深度优先搜索时，当前顶点是否被访问过。如果在同一次深度优先搜索中，已经被访问过，再次访问则说明存在有向环。
  • hasCycle
    如果为 true 表示存在环。
  • preorder 队列
    记录顶点前序，顶点在递归前入队。
  • postorder 队列
    记录顶点后序，顶点在递归后入队。
  • reverse 栈
    记录顶点逆后序，即拓扑排序；顶点在递归后入栈。
  • G 图
    有向无环图。
  • G.adj(v)
    顶点 v 所有邻接点序列。

参考：算法 4 的实现 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
private boolean[] marked;
private boolean[] onStack[];
private boolean hasCycle = false;
private Queue<Integer> preorder;
private Queue<Integer> postorder;
private Stack<Integer> reverse;

public TopologicalSorting(Digraph G) {
    preorder  = new Queue<Integer>();
    postorder = new Queue<Integer>();
    reverse = new Stack<Integer>();
    marked    = new boolean[G.V()];
    onStack   = new boolean[G.V()];
    
    for (int v = 0; v < G.V(); v++)
        if (!marked[v] && !hasCycle) dfs(G, v);
    
    if (hasCycle) reverse = null;
}

private void dfs(Digraph G, int v) {
    marked[v] = true;
    onStack[v] = true;
    // 递归前顶点入队
    preorder.enqueue(v);
    for (int w : G.adj(v)) {
        if (hasCycle) return;
        else if (!marked[w]) {
            dfs(G, w);
        }else if (onStack[w]){
            hasCycle = true;
            return;
        }
    }
    // 递归后顶点入队和入栈
    postorder.enqueue(v);
    reverse.push(v);
    
    onStack[v] = false;
}

// 获取有向无环图的拓扑排序
public Iterable<Integer> getTopologicalSort(){
    return reverse;
}

使用递归实现的拓扑排序，有深度优先搜索特性，所有排序结果是按照一条纵深线来排序的。

有向环检测

上述算法中，有向环的检测核心在同一次深度优先搜索 dfs 中，顶点 v 在遍历邻接点 w 时，如果再次访问到

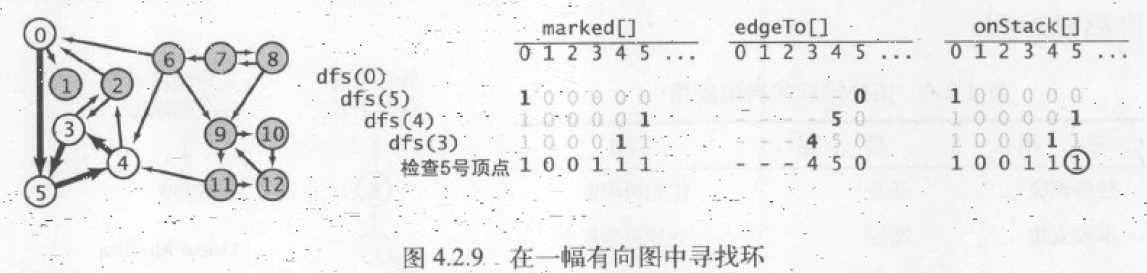
0092-dfs-cycle.png

广度优先搜索非递归实现

根据拓扑排序思路，使用入度数组来记录每个顶点的入度，入度为 0 时，顶点即为拓扑排序顺序。这种基于入度的拓扑排序，也称为 Kahn's algorithm 。

动图演示

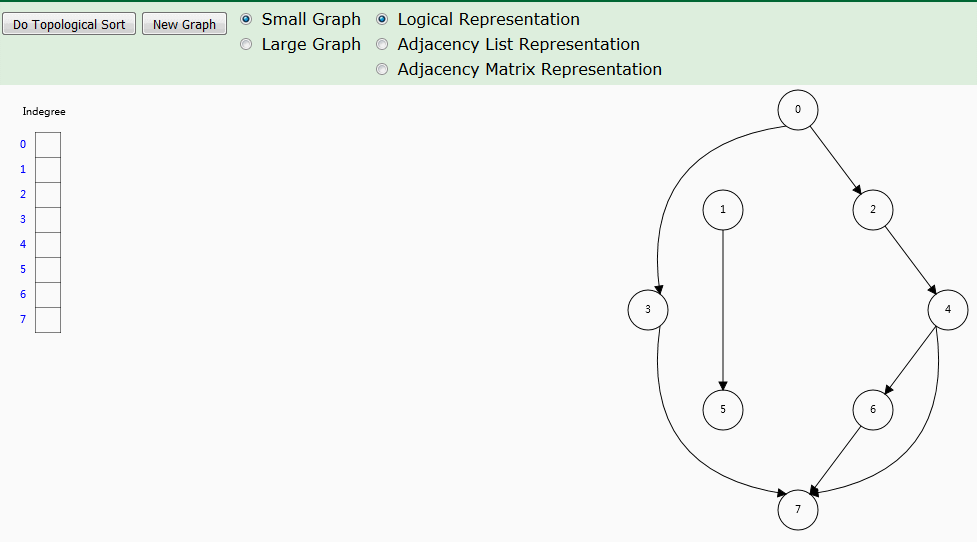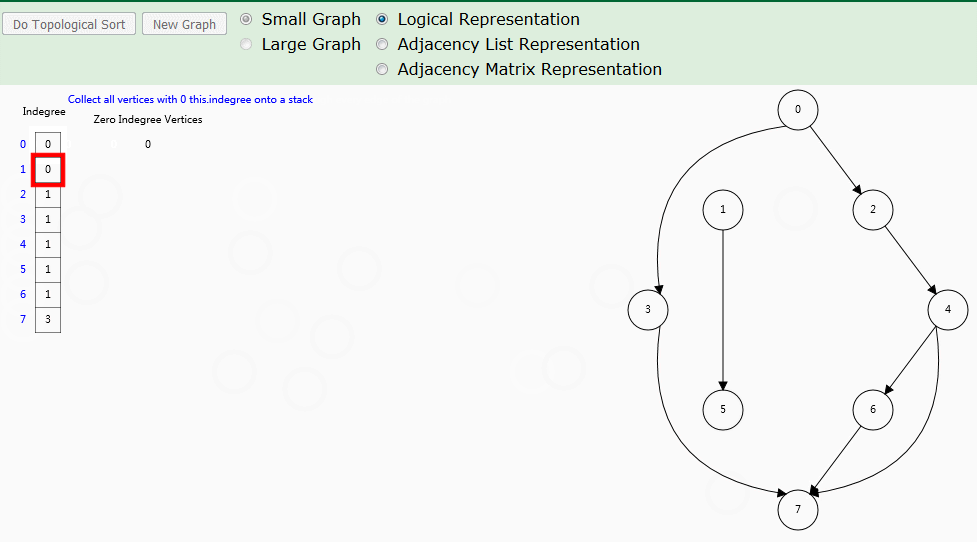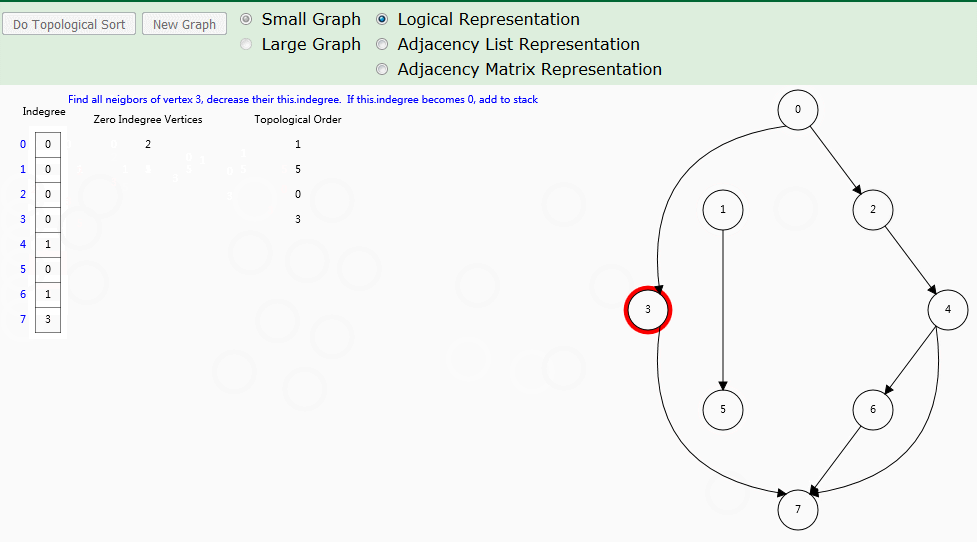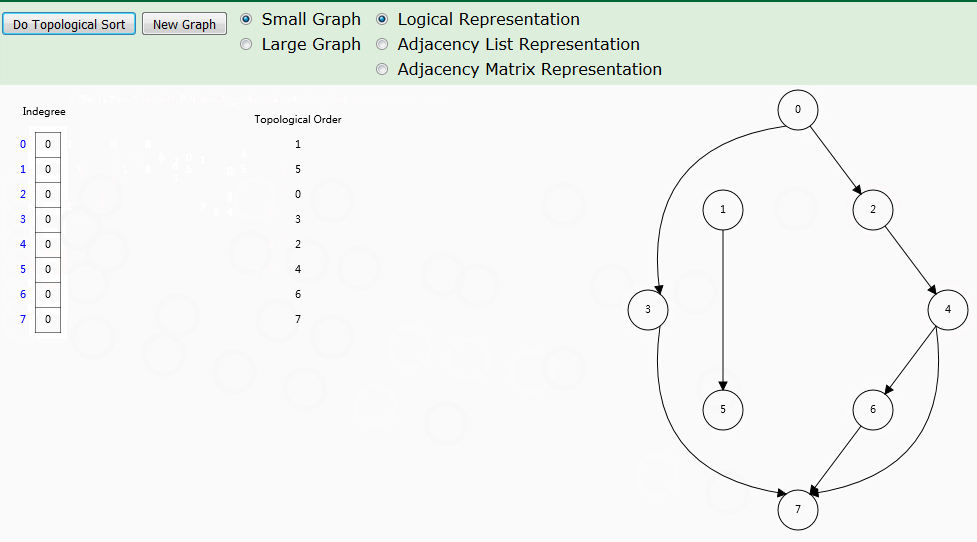
0092-topological-sorting-bfs-indegree.gif

算法解析

  • indegree[] 数组
    记录各个顶点当前入度，也是算法实现的核心数组。
  • zeroInDegreeQueue 队列
    辅助队列：记录入度为 0 的顶点入队顺序。循环取出顶点并访问其邻接点。
  • order 队列
    拓扑队列：记录入度为 0 的顶点入队顺序，也就是拓扑排序结果。如果
  • G 图
    有向无环图。
  • G.adj(v)
    顶点 v 所有邻接点序列。
  • G.indegree(v)
    顶点 v 的入度。

参考：算法 4 的实现 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
private int[] inDegree;
private Queue<Integer> zeroInDegreeQueue;
private Queue<Integer> order;

private void topologicalSort(Digraph G){
    inDegree = new int[G.V()];
    zeroInDegreeQueue = new LinkedList<>();
    order = new LinkedList<>();
    
    // 初始化入度数组，并将入度为 0 的顶点加入队列
    for (int v = 0; v < G.V(); v++){
        inDegree[v] = G.indegree(v);
        if (inDegree[v] == 0){
            zeroInDegreeQueue.offer(v);
        }
    }

    // 循环取出入度为 0 的顶点排序
    while (!zeroInDegreeQueue.isEmpty()){
        int node = zeroInDegreeQueue.poll();
        // 记录拓扑排序结果，即入度为 0 的顶点
        order.offer(node);
        for (int v : G.adj(node)) {
            inDegree[v]--;
            if (inDegree[v] == 0) {
                zeroInDegreeQueue.offer(v);
            }
        }
    }
    
    // 如果队列长度和顶点总数不等，表示有向图存在环
    if (order.size() != G.V()){
        order = null;
    }
}

使用入度数组的拓扑排序，有广度优先搜索的特性，所有排序结果是一层层的排出来的。

应用场景

  • 任务优先级排序
  • 任务调度

小结

环检测

不管是广度还是深度优先搜索，拓扑排序针对的是有向无环图。即使有向图中存在环，广度和深度优先搜索算法本身并不会报错或者无法执行，所以拓扑排序前后，需要判定有向图是否存在环！如果存在环，则排序结果是错误的，拓扑排序不存在。存在环的排序结果：

  • 深度优先搜索
    能得到所有顶点顺序，但是并没有体现拓扑排序的特点：图中任意一对顶点 u 和 v，若边 (u,v)∈E(G)，则 u 在线性序列中出现在 v 之前。也就是这个结果是错误的。
  • 广度优先搜索
    无法得到所有顶点顺序，在环里面的顶点输出不全。广度优先搜索使用的是入度数组来排序的，但是环中顶点入度将始终不会为 0，导致环中顶点不参与排序。

两种实现方式结果对比

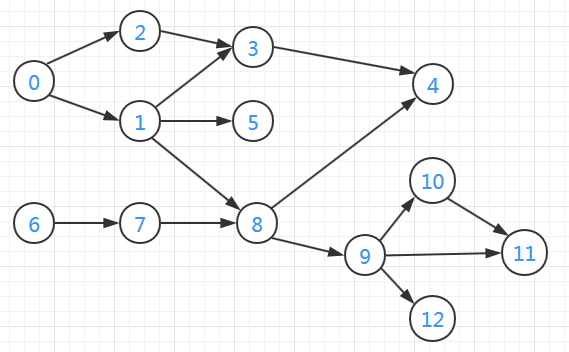
0092-topological-sorting-sample.png

  • 深度优先搜索
    拓扑排序结果：6, 7, 0, 2, 1, 8, 9, 12, 10, 11, 5, 3, 4 ，体现了排序纵深特性。
  • 广度优先搜索
    拓扑排序结果：0, 6, 1, 2, 7, 5, 3, 8, 9, 4, 10, 12, 11 ，体现了排序分层特性。

时间复杂度

不管是广度还是深度优先，实现拓扑排序的时间复杂度都为 O(V+E) 。

参考文档

0%