算法 - 强连通分量 Kosaraju 算法

发表于 | 分类于 | 阅读次数

Kosaraju 算法，也称为 Kosaraju-Sharir 算法：在线性时间内找到有向图的强连通分量。

强连通分量

如果两个顶点 v 和 w 是相互可达的，则称为它们为强连通的。强连通性将所有顶点分为一些平等的部分，每个部分都是由相互均为强连通的顶点的最大子集组成的；我们称这些最大子集为强连通分量。
强连通分量是基于顶点而不是边的，可以认为 V 个顶点的有向图，可能含有 1 ~ V 个强连通分量。一个强连通图，只含有一个强连通分量；一个有向无环图则含有 V 个强连通分量。

强连通分量，必定存在环中。

算法定义

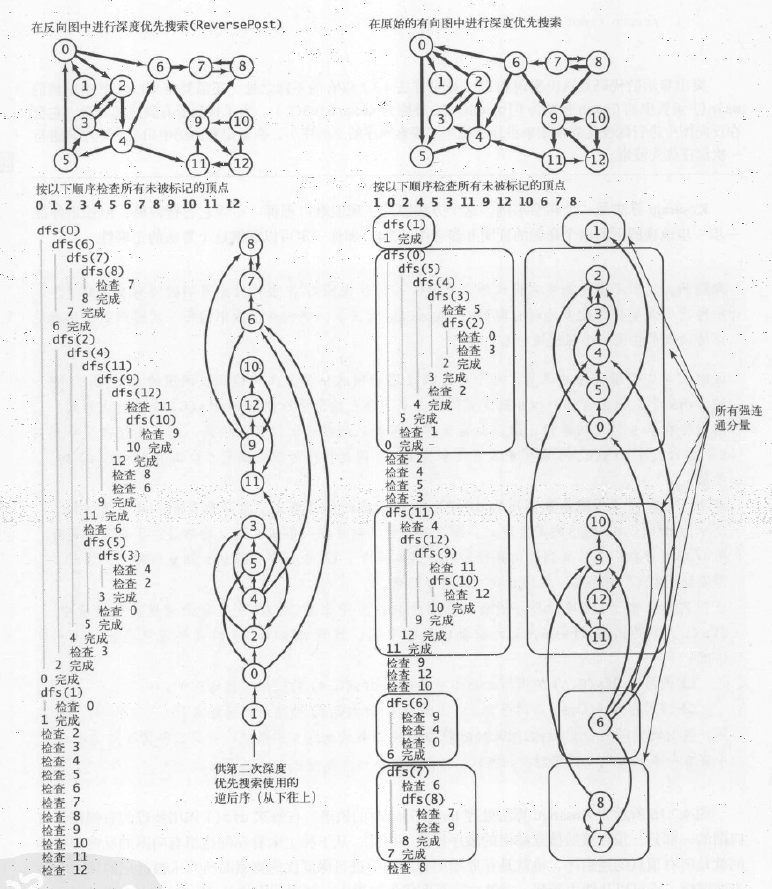
强连通分量的 Kosaraju 算法，使用深度优先 DFS 实现：

  • 在给定的有向图 G 中，计算反向图的顶点逆后序排序
  • 按照上一步逆后序中顶点的顺序，在 G 中按照深度优先搜索访问未被标记的顶点
  • 所有在同一个递归 DFS 调用中被访问到的顶点都在同一个强连通分量中

这里逆后序排序，不是拓扑排序，虽然算法类似，但是拓扑排序针对的是有向无环图，DFS 中会判断是否存在环，检测到环直接退出；而逆后序不检测环，会遍历所有顶点。

0093-scc-kosaraju-dfs.png

动画演示

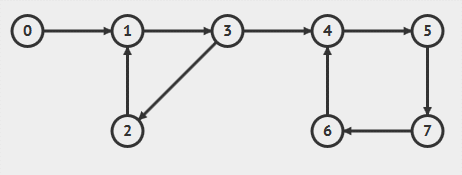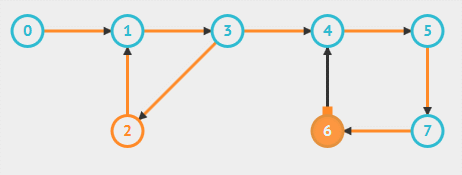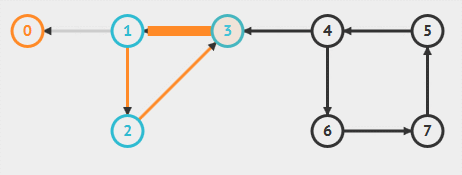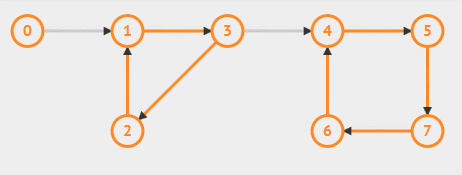
0093-scc-kosaraju.gif

动画演示和标准的 Kosaraju 算法有点不一样：它是先 DFS 遍历顶点得到逆后序排序，然后再将有向图置为反向图，按照逆后序排序取出顶点，深度优先搜索反向图。结果和 Kosaraju 算法一致。

算法实现

算法解析：

  • marked[] 数组
    记录当前顶点是否被访问过。
  • count
    记录有多少个强连通分量。
  • id[] 数组
    记录当前顶点属于第几个强连通分量。
  • G.reverse()
    有向图 G 的反向图：即将所有边的指向全部反过来。
  • ReversePostSort.getSort
    使用深度优先搜索获取顶点的逆后序排序。 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
// Kosaraju-Sharir 强连通分量算法
public class KosarajuSharirSCC {
    private boolean[] marked;
    private int[] id;
    private int count;
    
    public KosarajuSharirSCC(Digraph G) {
        marked = new boolean[G.V()];
        id = new int[G.V()];

        ReversePostSort reverse = new ReversePostSort(G.reverse());
        for (int v : reverse.getSort()) {
            if (!marked[v]) {
                dfs(G, v);
                count++;
            }
        }
    }
    
    private void dfs(Digraph G, int v) { 
        marked[v] = true;
        id[v] = count;
        for (int w : G.adj(v)) {
            if (!marked[w]){
                dfs(G, w);
            }
        }
    }
}

// 深度优先搜索，得到顶点的逆后序排序
public class ReversePostSort{
    private boolean[] marked;
    private Stack<Integer> reversePostOrder;
    
    public ReversePostSort(Digraph G) {
        reversePostOrder = new Stack<Integer>();
        marked = new boolean[G.V()];
        
        for (int v = 0; v < G.V(); v++)
            if (!marked[v]) dfs(G, v);
    }
    
    private void dfs(Digraph G, int v) {
        marked[v] = true;
        for (int w : G.adj(v)) {
            if (!marked[w]) {
                dfs(G, w);
            }
        }
        // 递归后顶点入栈
        reversePostOrder.push(v);
    }
    
    // 获取有向无环图的拓扑排序
    public Iterable<Integer> getSort(){
        return reversePostOrder;
    }
}

小结

  • 时间复杂度
    时间复杂度为 O(V+E) 。

参考文档

0%