算法 - 强连通分量 Tarjan 算法

发表于 | 分类于 | 阅读次数

Tarjan 算法是 Robert Tarjan （罗伯特·塔扬）发明的，只通过一次深度优先搜索就能计算出有向图的强连通分量，而 Kosaraju 算法需要做两次 DFS 加上计算图的反向图。

算法定义

Tarjan 算法是基于对图深度优先搜索的算法，每个强连通分量为搜索树中的一棵子树。搜索时把当前搜索树中未处理的节点加入一个堆栈，回溯时可以判断栈顶到栈中的节点是否为一个强连通分量。定义两个重要数组：

  • dfn(v) 为顶点 v 被搜索的次序号
  • low(v) 为顶点 v 被搜索的次序号，或者** v 的子树能够追溯到的最早的栈中顶点的次序号**（这句话非常费解，没弄明白！）

本文算法实现及分析的有向图：

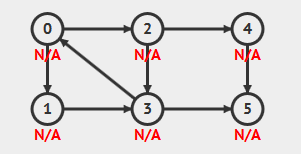
0094-scc-tarjan-digraph.png

动画演示

0094-scc-tarjan.gif

visualgo 上动画演示的伪代码是错误的！但是动画实际执行的结果是对的。

算法解析

算法中的几个重要的变量：

  • marked[] 数组
    记录当前顶点是否被访问过。
  • stack 栈
    辅助变量：记录同一个强连通分量中的所有顶点。当 DFS 第一次访问顶点时，该顶点入栈；当顶点 v 的强连通分量条件满足时，栈中顶点逐个出栈，直到顶点 v 也出栈。
  • onStack[] 数组
    记录当前顶点是否在栈中。
  • dfn[] 数组
    记录顶点被访问的次序号，dfn[v]=5 表示顶点 v 是第 5 个被访问的顶点。
  • low[] 数组
    low[v] 值的计算很复杂，搜索时从顶点 v 访问顶点 w 则 low[v]=min{low[v], dfn[w]} ；回溯时顶点 v 从顶点 w 回溯，则 low[v]=min{low[v], low[w]}。可能帮助理解的概念：
    横插边：连接到已经出栈的节点的边；
    后向边：连接到已在栈中节点的边；
    树枝边：在搜索树中的边。
  • count
    强连通分量的个数。

Tarjan 算法涉及到深度优先搜索 DFS 的两个过程：搜索过程和回溯过程。

  • DFS 遍历有向图中所有的顶点，并将顶点压入栈
  • DFS 搜索过程中，对于从顶点 v 访问顶点 w ：如果顶点 w 没有被访问过，对 w 进行 DFS 遍历；如果 w 被访问过且 w 在栈中，更新 low[v] 的值：low[v]=min{low[v], dfn[w]}
  • DFS 回溯过程中，对于顶点 v 从顶点 w 回溯，更新 low[v] 的值：low[v]=min{low[v], low[w]}
  • 不管是搜索过程还是回溯过程，如果顶点 v 满足 dfn[v] == low[v]，则栈中顶点 v 之上的顶点是一个强连通分量！栈中元素逐个出栈，直到顶点 v 出栈 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
public class TarjanSCC {

    private boolean[] marked;
    private int[] dfn;
    private int[] low;               // low[v] = low number of v
    private int pre;                 // preorder number counter
    private Stack<Integer> stack;
    private boolean[] onStack;
    private int count;

    public TarjanSCC(Digraph G) {
        marked = new boolean[G.V()];
        stack = new Stack<Integer>();
        low = new int[G.V()];
        dfn = new int[G.V()];
        onStack = new boolean[G.V()];
        
        // 深度优先搜索
        for (int v = 0; v < G.V(); v++) {
            if (!marked[v]) tarjan(G, v);
        }

    }
    
    private void tarjan(Digraph G, int v){
        marked[v] = true;
        // 记录顶点被访问的次序号
        dfn[v] = low[v] = pre++;
        stack.push(v);
        onStack[v] = true;
        for (int w : G.adj(v)){
            if (!marked[w]) {
                // 递归深度优先搜索
                tarjan(G, w);
                if (low[v] > low[w])
                    low[v] = low[w];
            } else if (onStack[w] && low[v] > dfn[w]){
                low[v] = dfn[w];
            }
        }

        // 顶点 v 满足强连通分量条件
        // 栈中顶点 v 之上的所有顶点都在同一个强连通分量中
        // 栈中顶点出栈，直到顶点 v 出栈
        if (dfn[v] == low[v]){
            int w;
            do {
                w = stack.pop();
                onStack[w] = false;
                id[w] = count;
            } while (w != v);
            count++;
        }
    }
}

《算法 4》的作者将 low[] 数组做了简化：low[v]=min{low[v], low[u]} ，也没有使用 dfn[] 数组。这样得出的 low[] 结果：同一个强连通分量中所有顶点的 low[] 值相同。本文参考的是 wiki: Tarjan Algorithms 的伪代码，网上大部分实现都是基于这份伪代码。
参考：github tarjanscc 代码

图解

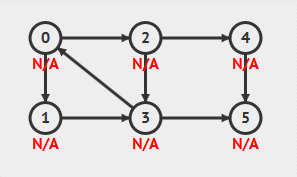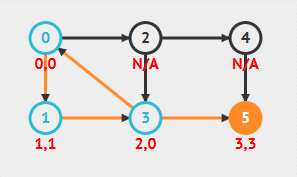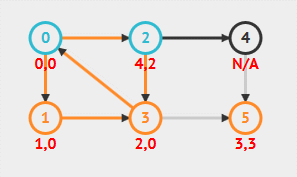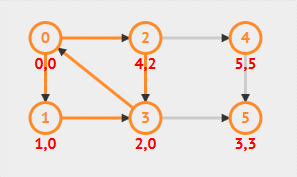
Tarjan 算法的 dfn[] 值很好理解，但是 low[] 并不好理解，特别是代表的含义，本文也没弄明白！！现在通过代码来图解分析 low[v] 的值。深度优先搜索顺序为：0, 1, 3, 5, 2, 4 ，重点分析三个顶点 3, 1, 2。

顶点 3

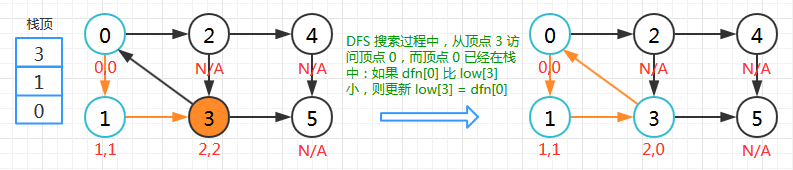
0094-scc-tarjan-v-3.png

顶点 3 的 low 值是在搜索时变化的，回溯没有更新。DFS 搜索过程中，从顶点 3 访问顶点 0，而顶点 0 已经在栈中：如果 dfn[0] < low[3]，则更新 low[3] = dfn[0]，所以 low[3]=0 。

顶点 1

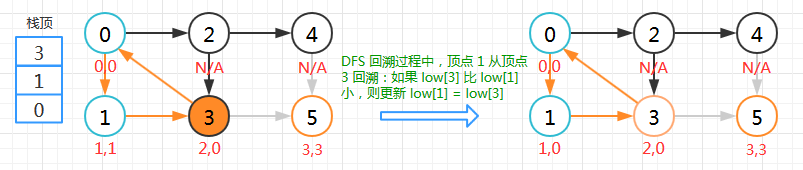
0094-scc-tarjan-v-1.png

顶点 1 的 low 值是在回溯时更新的，搜索时因为是第一次访问直接赋值次序号。DFS 回溯过程中，顶点 1 从顶点 3 回溯：如果 low[3] < low[1]，则更新 low[1] = low[3]，所以 low[1]=0 。

顶点 2

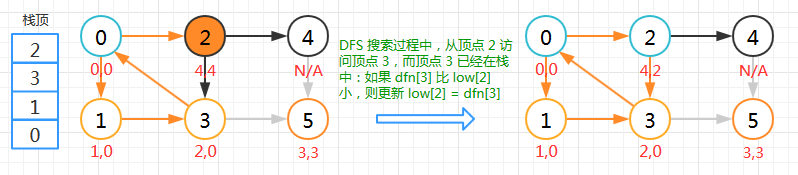
0094-scc-tarjan-v-2.png

顶点 2 的 low 值是在搜索时变化的，回溯没有更新。DFS 搜索过程中，从顶点 2 访问顶点 3，而顶点 3 已经在栈中：如果 dfn[3] < low[2]，则更新 low[2] = dfn[3]，所以 low[2]=2。
low[2] 的值如果按照定义：最早栈中顶点次序号，应该为 0？但是根据算法实现思路推算，以及实际调试的结果： low[2]=2 。这也是为什么没弄明白 low 值含义的原因！

小结

  • 复杂度
    Tarjan 算法的时间复杂度也为 O(V+E)，虽然比 Kosaraju 算法计算量小，但是并没有 Kosaraju 算法容易理解。
  • 强连通
    示例中顶点 1 3 4 和 顶点 1 2 4 都是强连通图，但是只有 1 2 3 4 才是强连通分量（相互连通顶点的最大子集）。

参考文档

0%