算法 - 并查集

发表于 | 分类于 | 阅读次数

并查集 Union-Find ，也称为不相交集。

概念

不相交集合数据结构

一个不相交集合数据结构 disjoint-set data structure 维护了一个不相交动态集的集合 S={S1, S2, S3, ..., Sk}。我们用一个代表 representative 来标识这个集合，它是这个集合的某个成员。这个数据结构支持下面三个操作：

  • MAKE-SET(x) ：集
    建立一个新的集合，它的唯一成员（因而为代表）是 x。因为各个集合是不相交的，故 x 不会出现在别的某个集合中。
  • UNION(x, y) ：并
    将包含 x 和 y 的两个动态集合（表示为 Sx, Sy）合并为一个新的集合，即这两个集合的并集。假定在操作之前这两个集合是不相交的。虽然 UNION 的很多实现中特别地选择 Sx 或 Sy 的代表作为新的代表，然而结果集的代表可以是 Sx U Sy 的任何成员。
  • FIND-SET(x) ：查
    返回包含 x 的（唯一）集合的代表。也就是代表 x 所在集合的元素。

这种数据结构也称为并查集。可以使用链表结构实现，但是更多采用的是堆存储结构（即用数组表示一棵树）。

不相交集合森林

在一个不相交集合更快的实现中，我们使用有根树来表示集合，树中每个节点包含一个成员，每棵树代表一个集合。在一个不相交集合森林 disjoint-set forest 中，每个成员仅指向它的父节点。每棵树的根包含集合的代表，并且是其自己的父节点。

应用场景

  • 确定无向图的连通分量（但并不需要知道连通路径）
  • 确定无向图中，两个顶点是否是连通的

并查集的特点有点像优先队列：只需要知道最小值，但并不需要完全排序。而并查集只需要知道两个顶点是否连接，但并不要这两个顶点的路径。

秩 rank

秩：记录树高度的一个上界（这颗树曾经达到过的最高树高），是树高的一个估计值，并不准确。
常见错误理解：秩为当前节点为根的树，该树的树高；秩为当前节点所在树中，根节点的树高。这些说法都不正确，因为秩是一个估计值，所以并不能准备代表任何节点，任何数的树高，仅仅是一个估计值，而且是曾经的上界。

算法定义

按秩合并

按秩合并 union by rank：让具有较小秩的根，指向具有较大秩的根。这样两个根的秩都不会变化。

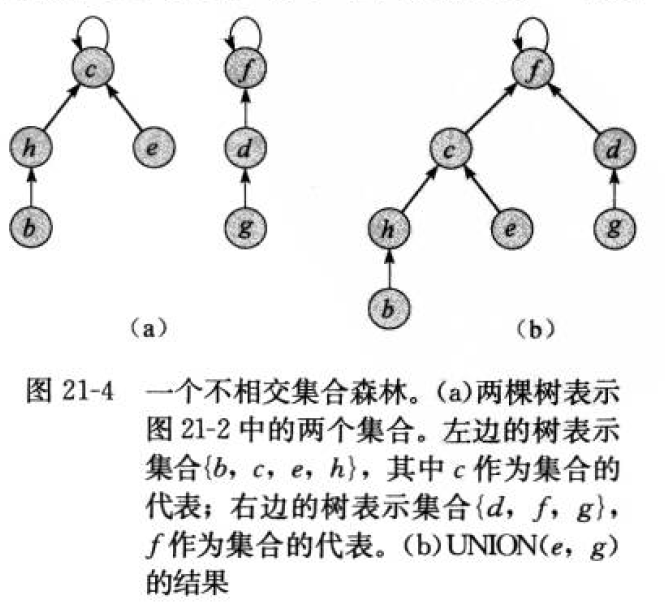
0095-union-find-union-by-rank.png

路径压缩

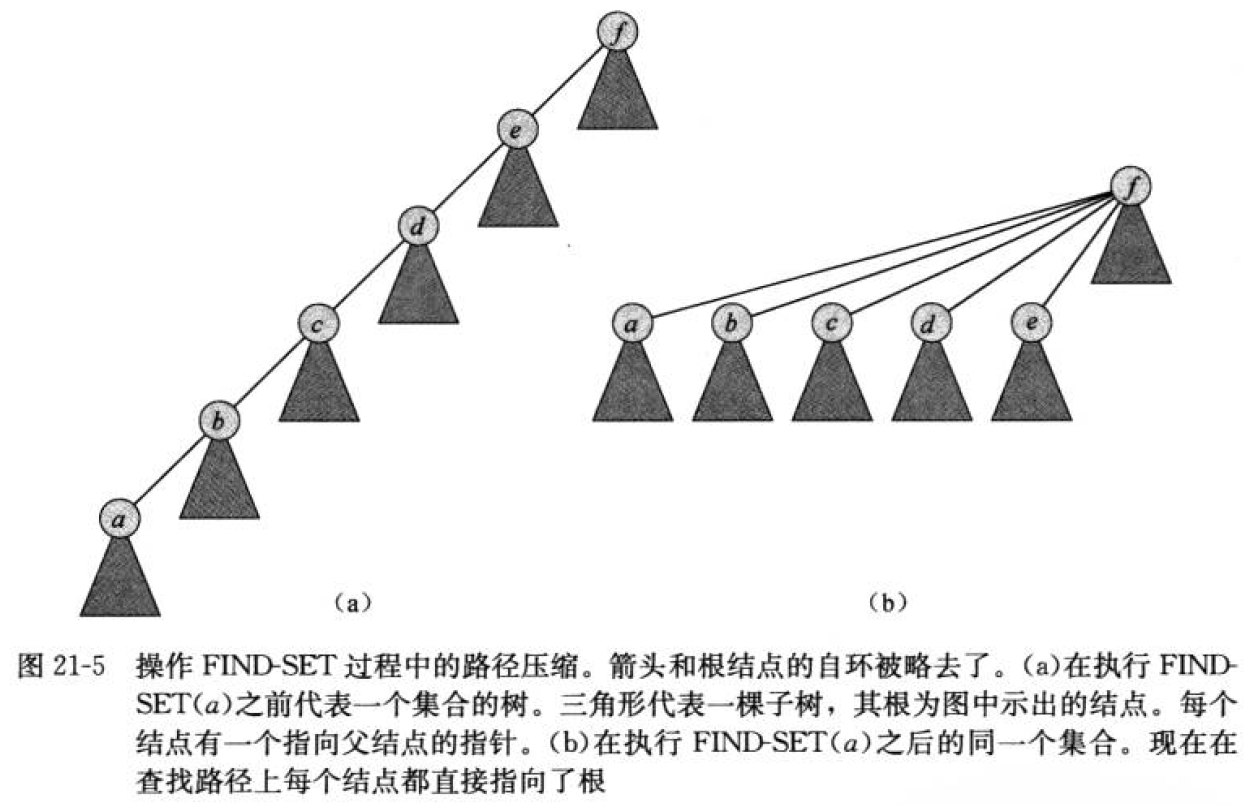
路径压缩 path compression：使查找路径上的每个节点都指向根。路径压缩并不改变任何节点的秩！
这里非常容易理解错误，因为路径压缩实际上压缩了树高，为什么却没有改变秩呢？我们来看《数据结构与算法分析–C语言描述》这本书中的解释：

路径压缩与“按大小求并”完全兼容，但不完全与“按高度合并”兼容，因为路径压缩可以改变树的高度。我们根本不清楚如何有效地重新计算它们（树高）。答案是不去计算！！此时，对于每棵树存储的高度是估计的高度（有时称为秩 rank）。但实际上“按秩合并”理论上和“按大小合并”效率上是一样的。不仅如此，高度的更新也不如大小的更新频繁。（第八章：不相交集 ADT - 路径压缩）

也就是说：因为秩的定义是树曾经的最高值，所以路径压缩时即使减小了树高，也不用去改变秩，并且实际上也无法计算树的准确高度。

0095-union-find-path-comprossion.png

动画演示

按秩合并

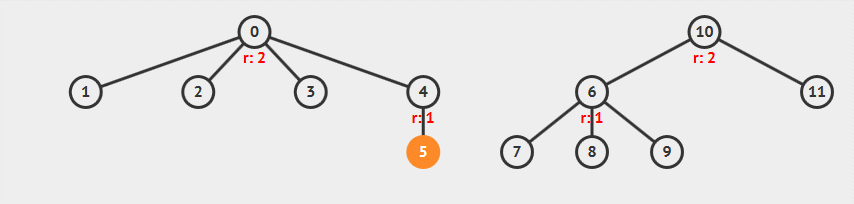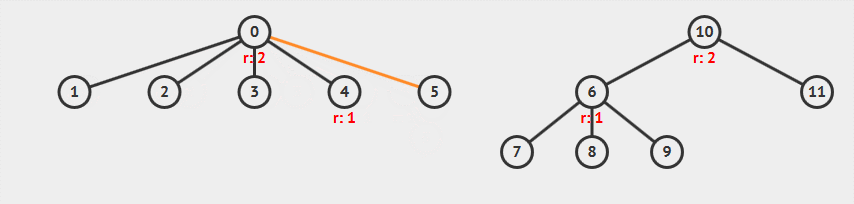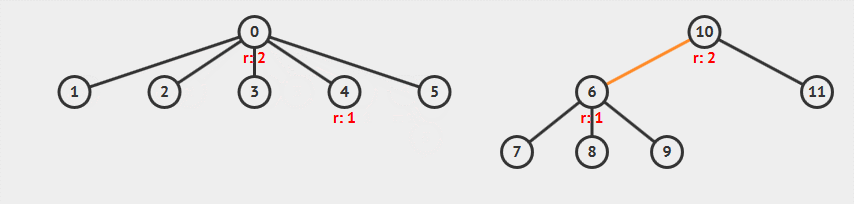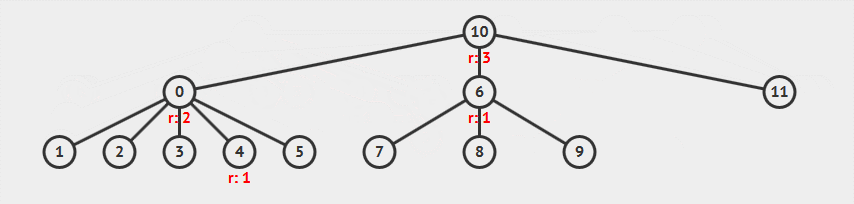
0095-union-find-union.gif

从图中可以看到：

  • 合并顶点 5 和顶点 6，先查找两个顶点的根，并将较小秩的树并到较大秩的树中
  • 合并两棵树后，整棵树高度增长，顶点 10 的秩增加 1

路径压缩

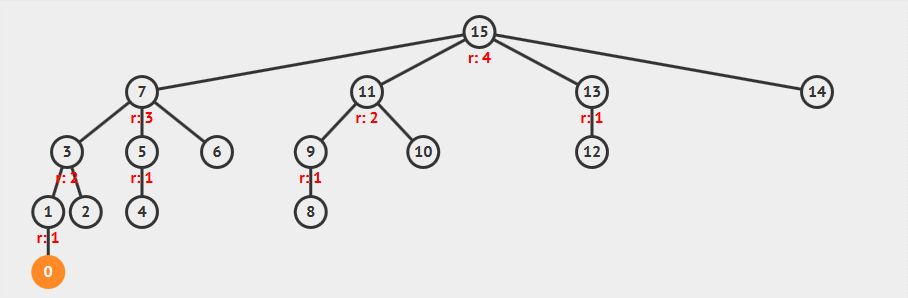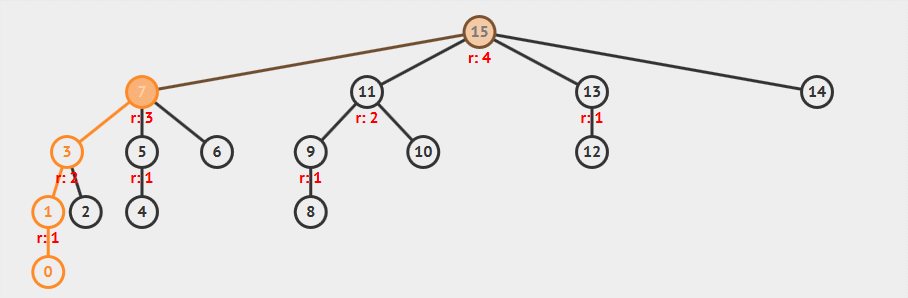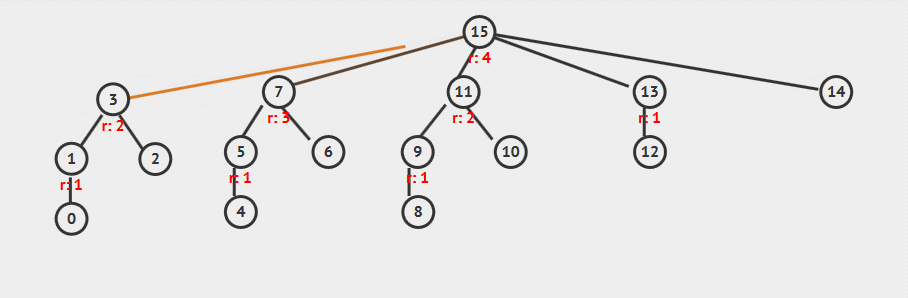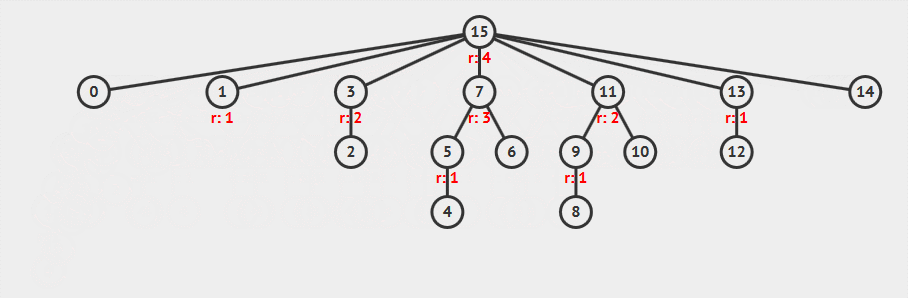
0095-union-find-find.gif

从图中可以看到：

  • 查找顶点 15 时，查找路径上的所有节点的父节点都设置为根节点
  • 顶点 7 的树高实际减小了一层，但是秩 rank 并没有改变

算法解析

标准实现

两个关键数组：

  • parent[] 数组
    记录当前位置节点的父节点。
  • rank[] 数组
    以当前位置节点为根的树，记录它的秩。对秩的理解很大程度的影响了对算法的理解，因为是估计值，所以在 find 时，即使压缩了树高，也并没有更新 rank 的值（同时也无法准确计算它的值）。
  • count
    记录有多少个连通分量，或者说有多少棵树。 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
public class UF {
    // parent[i] = parent of i
    private int[] parent;
    // rank[i] = rank of subtree rooted at i (never more than 31)
    private byte[] rank;   
    private int count;

    // MAKE-SET
    public UF(int n) {
        if (n < 0) throw new IllegalArgumentException();
        count = n;
        parent = new int[n];
        rank = new byte[n];
        // 建立并查集时，每个顶点的父节点都是自己
        // 每个顶点的秩都是 0
        for (int i = 0; i < n; i++) {
            parent[i] = i;
            rank[i] = 0;
        }
    }

    // FIND-SET(x)
    public int find(int p) {
        int r = p, t;

        // r: root node.
        // 查找到根节点
        while (parent[r] != r)
            r = parent[r];

        // path compression
        // 将查找路径上所有节点的父节点都设置为根
        while (parent[p] != r) {
            t = parent[p];
            parent[p] = r;
            p = t;
        }

        return r;
    }

    // 判断两个顶点是否连通
    public boolean connected(int p, int q) {
        return find(p) == find(q);
    }

    // UNION
    public void union(int p, int q) {
        int rootP = find(p);
        int rootQ = find(q);
        // 如果两个顶点在同一棵树中，不需要合并
        if (rootP == rootQ) return;

        // make root of smaller rank point to root of larger rank
        // 较小秩的根，其父节点设置为较大秩的根
        if      (rank[rootP] < rank[rootQ]) parent[rootP] = rootQ;
        else if (rank[rootP] > rank[rootQ]) parent[rootQ] = rootP;
        else {
            parent[rootQ] = rootP;
            // 树的高度增加一层
            rank[rootP]++;
        }
        count--;
    }
}

代码参考：算法4 UF.java

路径压缩的其他实现

  • 递归实现

    1
    2
    3
    4
    5
    6
    public int find(int p){
        if (p != parent[p]){
            parent[p] = find(parent[p]);
        }
        return parent[p];
    }

  • 减半压缩
    《算法4》中使用的 find 算法就是这种减半压缩，只将当前节点链接到爷爷节点，下次再从爷爷节点链接到爷爷的爷爷节点，如此反复直到根节点。也就是说，当前节点的父节点并没有直接链接到根节点，以及爷爷的父节点也没有链接到根节点。只需要循环遍历一次，就实现了路径压缩同时查找到根节点。

    1
    2
    3
    4
    5
    6
    7
    8
    public int find(int p) {
        validate(p);
        while (p != parent[p]) {
            parent[p] = parent[parent[p]];    // path compression by halving
            p = parent[p];
        }
        return p;
    }

测试数据

parent 指的是父节点相同的节点个数，指向根节点或者没有被路径压缩到根节点的节点。

实现方式 数据大小 rank parent 连通分量
路径全压缩 100000 9 41650 6
路径减半压缩 100000 9 48023 6
路径全压缩 625 5 83 2
路径减半压缩 625 5 88 2

小结

  • 动态性
    并查集连通性是动态的，并不需要先将完整的关系导入，可以边合并边来查找。
  • 扁平型
    并查集生成的森林中，每棵树都接近扁平，参考测试数据，百万数据的秩也是个位数，实际树高更低。
  • 时间复杂度
    除了构造并查集时，时间复杂度为 N；按秩合并和路径压缩查找的时间复杂度基本能达到常数级别，效率非常高。

参考文档

0%