算法 - 最小生成树以及 Prim 算法

Prim 算法 - 普里姆算法，用来计算加权无向图的最小生成树。又被称为 DJP 算法、亚尔尼克算法、普里姆－亚尔尼克算法。

概念

基础概念

无向图的连通图：从任意一个顶点都存在一条路径到达另外任意一个顶点，则这幅图是连通图。
生成树：包含所有顶点的无环连通子图，称为生成树。
最小生成树 MST: Minimum Spanning Tree ：也是最小权重生成树的简称。一幅加权无向图，对应的生成树中，树中所有边的权值之和最小。

最小生成树的目的是：在加权无向图中，找出 V-1 条边，且它们的顶点构成无环连通子图，并且这些边的权值之和最小。

最小生成树

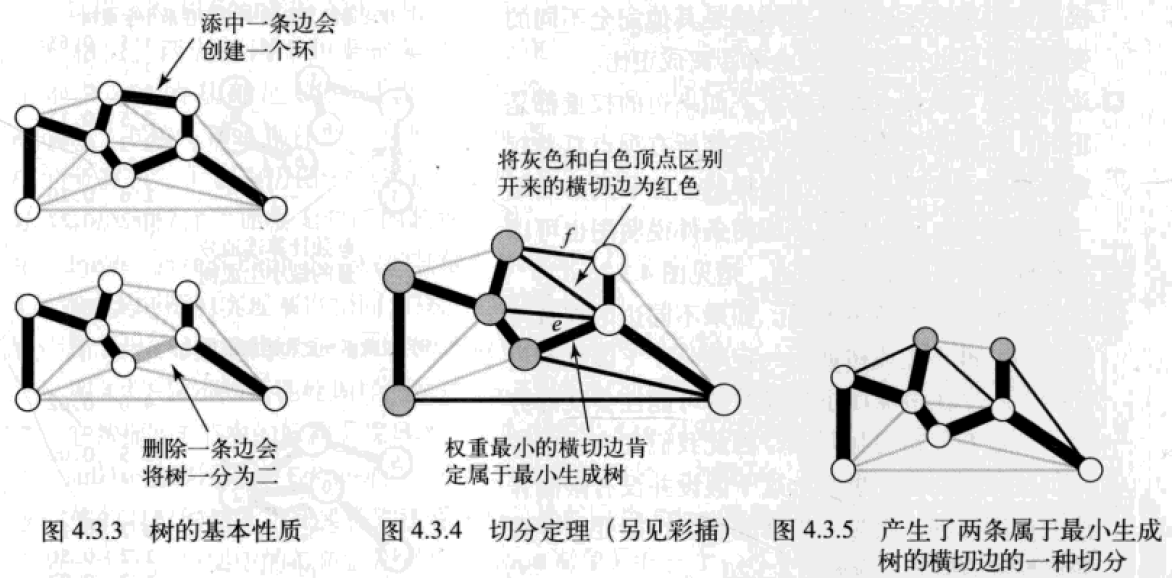
• 切分：将图的所有顶点分为两个非空且不重复的两个集合；切分就是将图分成二分图
• 横切边：是一条连接两个属于不同集合的顶点的边
• 切分定理：在一幅加权图中，给定任意的切分，它的横切边中的权重最小者必然属于图的最小生成树；是最小生成树算法的基本定理

算法定义

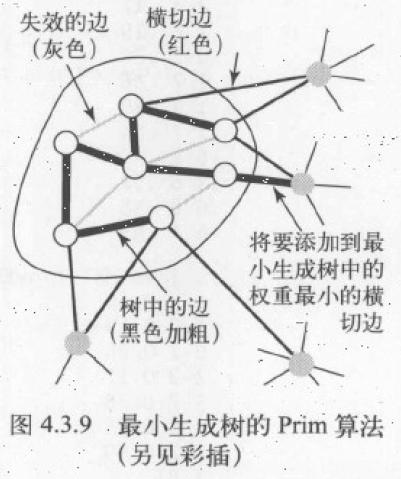
Prim 算法的每一步都会为一颗生长中的数添加一条边：最开始这颗树只有一个顶点（起点），然后向它添加 V-1 条边，每次总是将下一条连接树中顶点与不在树中的顶点且权重最小的边（也就是横切边权重最小者），加入到树中。

• 选取任意顶点作为起点，则该顶点为树中顶点
• 从非树顶点集合中，找出横切边权重最小者，根据切分定理，这条边必然属于最小生成树；则边的另一个顶点也成为树中顶点
• 循环选取横切边，直到找到 V-1 条边（所有顶点都加入到树中），这些边构成最小生成树

应用场景

如：电路图中，连接多个组件的针脚，使用最小生成树，来确保连接最短。

Prim 延时实现

动画演示

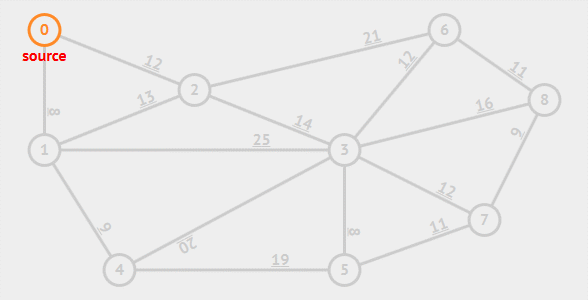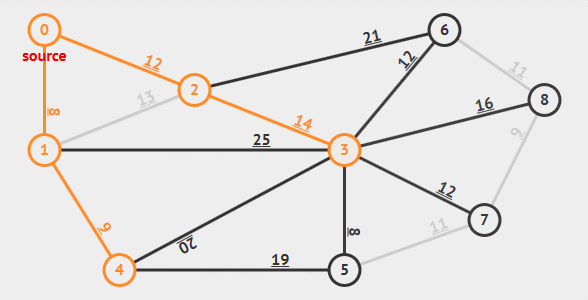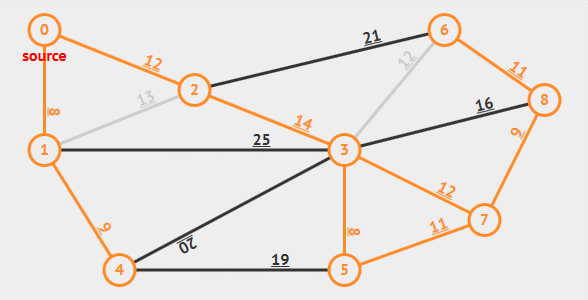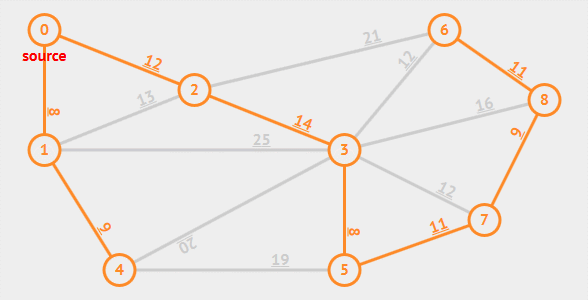
算法解析

• marked[] 数组
  记录当前顶点是否被扫描过。
• Queue<Edge> mst 对列
  Edge 表示图中的边，mst 记录最小生成树所有的边，长度为 V-1 。
• weight
  最小生成树的总权重。
• MinPQ<Edge> pq 优先队列
  小根堆，记录图中所有的边。
• G.adj(v)
  顶点 v 所有邻接点对应的边。

切分：也就是 marked 数组，如果顶点已经被扫描，则为 true。所以 marked 数组将所有顶点分成了两个非空且不重复的集合：{扫描过，未被扫描过} 。
横切边：一条边的两个顶点 v-w，其中顶点 v 已经被扫描，顶点 w 未被扫描，即 v, w 属于两个不同集合，而这条边就是横切边。如下算法实现中，始终取出小根堆中最小权重的边，当判断这条边是横切边时，则这条边属于最小生成树。

算法核心思路：

• 每个顶点都会有一条最小权重的横切边，逐个扫描顶点找出这条横切边
• 扫描顶点 v 时，该顶点的所有边中，如果另一个顶点没有被扫描过，则将边压入小根堆；也就是小根堆存储了图中所有的边
• 循环取出小根堆中最小的边，判断边两端顶点是否被扫描过（如果有一个顶点没有被扫描，说明这条边是横切边，且权重最小），即判断是否为横切边
• 将权重最小的横切边加入最小生成树队列中；继续扫描横切边中未被扫描的顶点，并将该顶点的边加入优先队列
• 优先队列循环出队，直到队列为空，或者最小生成树队列中有 V-1 条边

public class LazyPrimMST {

    private double weight;
    private Queue<Edge> mst;
    private boolean[] marked; 
    private MinPQ<Edge> pq;

    public LazyPrimMST(EdgeWeightedGraph G) {
        mst = new Queue<Edge>();
        pq = new MinPQ<Edge>();
        marked = new boolean[G.V()];
        // 逐个顶点扫描，找出权重最小横切边
        for (int v = 0; v < G.V(); v++)
            if (!marked[v]) prim(G, v);

    }

    // run Prim's algorithm
    private void prim(EdgeWeightedGraph G, int s) {
        scan(G, s);
        // better to stop when mst has V-1 edges
        while (!pq.isEmpty()) {
            // 取出权重最小的边
            Edge e = pq.delMin();
            int v = e.either(), w = e.other(v);
            assert marked[v] || marked[w];
            // 如果边的两个顶点都被扫描过，则继续出队
            if (marked[v] && marked[w]) continue;
            // 否则这条边为横切边，且权重最小
            // 将这条最小权重横切边，加入到最小生成树中
            mst.enqueue(e);
            weight += e.weight();
            // 沿着边的两端继续扫描
            if (!marked[v]) scan(G, v);
            if (!marked[w]) scan(G, w);
        }
    }

    // add all edges e incident to v onto pq 
    // if the other endpoint has not yet been scanned
    private void scan(EdgeWeightedGraph G, int v) {
        // 扫描顶点 v
        marked[v] = true;
        for (Edge e : G.adj(v))
            if (!marked[e.other(v)]) pq.insert(e);
    }
}

参考代码：LazyPrimMST

特点

优先队列存储所有的边，逐个取出时再判断是否为横切边（延时判断）。

Prim 即时实现

即时实现主要区别在于：优先队列中始终存储的是非树顶点到树中的最小权重横切边。

• 失效边
  
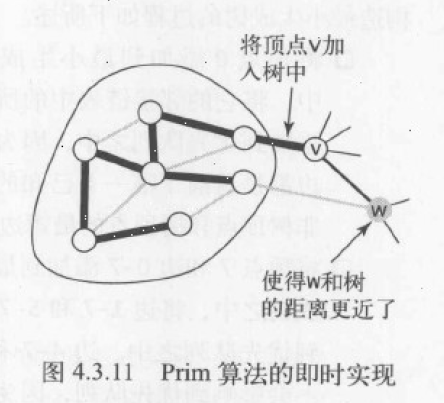
• 优先队列
  
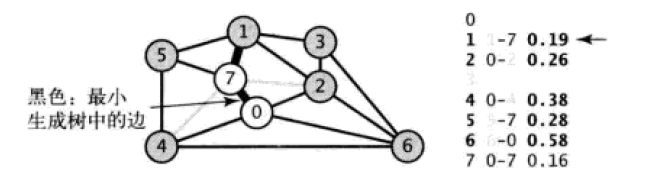
  从图解中看到四条边：7-2, 7-4, 0-4, 0-2 都是横切边，而 7-2 和 7-4 已经失效，因为 0-4 和 0-2 权重更小；对于优先队列始终只存储非树顶点 2, 4 到树中 0, 7 的最小权重横切边，即只存储 0-4, 0-2 。

图解

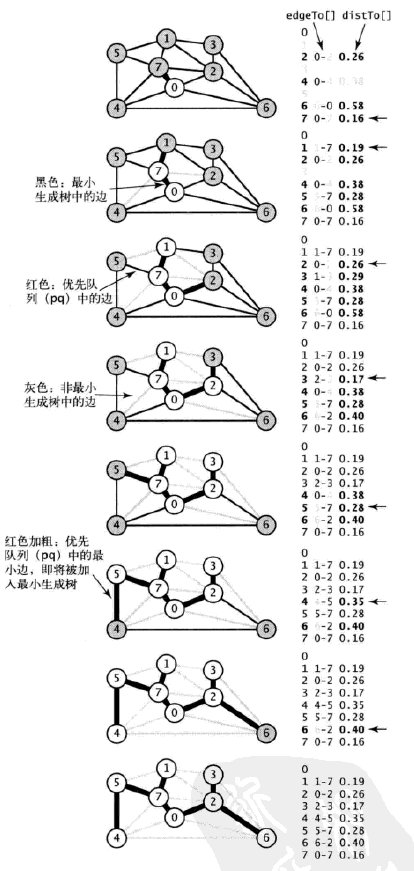
动画演示

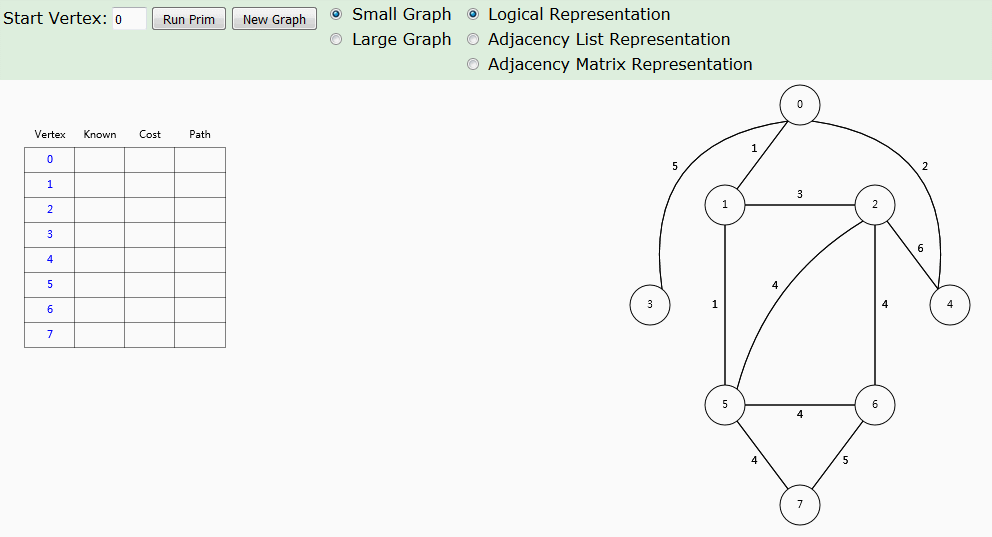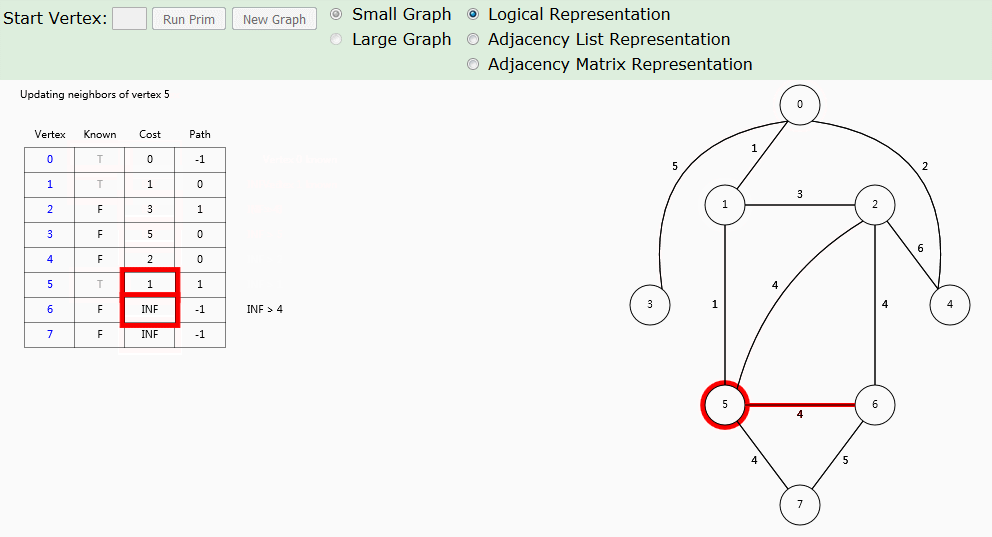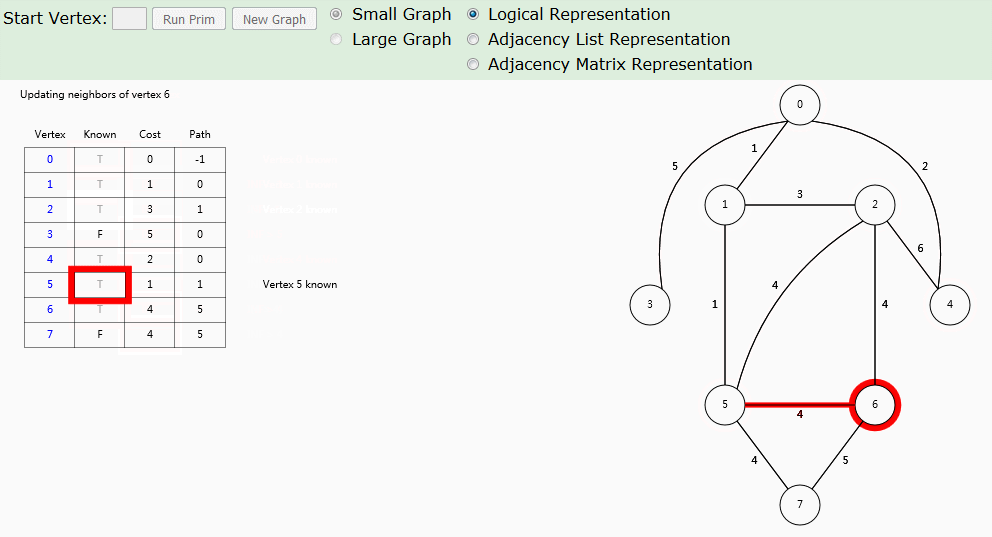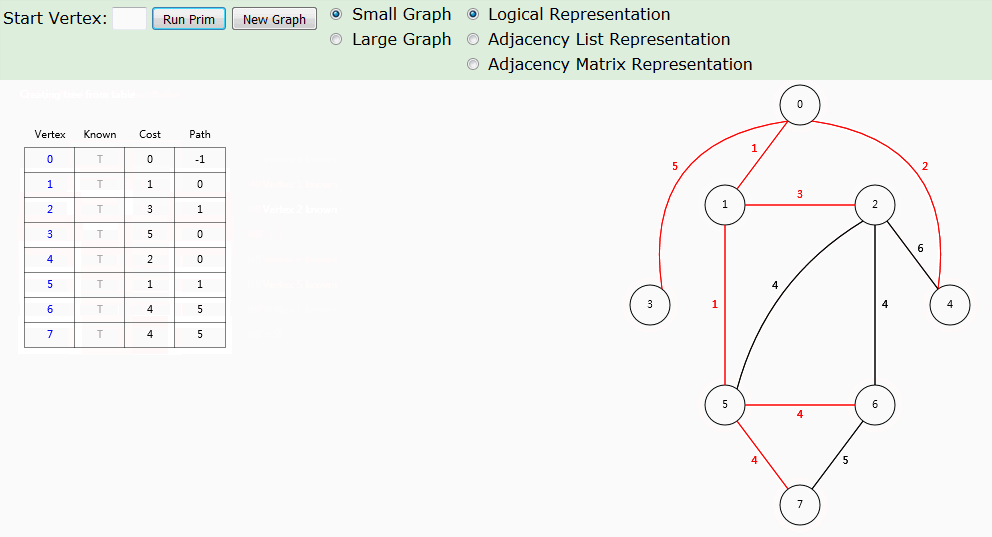
这段动画更适合在网站上逐步显示，更便于理解动画算法步骤。

算法实现

• marked[] 数组
  记录当前顶点是否被扫描过。
• weight
  最小生成树的总权重。
• edgeTo[] 数组和 distTo[] 数组
  如果顶点 v 不在树中，但至少还有一条边和树相连。则 edgeTo[v] 是将顶点 v 与树相连的最短边，distTo[v] 为这条边的权重。
• PriorityQueue<Edge> pq 优先队列
  小根堆，记录图中非树顶点到树中的最小权重横切边，堆顶的最小权重横切边满足切分定理，而这条边的非树顶点就是下一个被添加到树中的顶点；该优先队列长度不会超过顶点数。
• G.adj(v)
  顶点 v 所有邻接点对应的边。

算法核心思路：

• 将 distTo[] 数组初始化为无限大，即所有边都不属于树
• 从加权无向图中任意指定起点 s，扫描该顶点及其对应的邻接边
• 如果邻接边的顶点被扫描过，则继续遍历其他邻接边顶点；如果没有被扫描过，则判断这条边是否比记录的小
• 如果这条边为权重更小，则更新 distTo[] 权重；将失效的边从优先队列中删除，并添加这条有效横切边到优先队列中
• 循环从优先队列中取出最小键（即满足切分定理的最小权重横切边），而和它关联的顶点 w 就是下一个被添加到树中的顶点；直到优先队列中所有的横切边都被取出，最小生成树生长完成

public class PrimMST {
    private Edge[] edgeTo;
    private double[] distTo;
    private boolean[] marked;
    private PriorityQueue<Edge> pq;
    private Double weight;

    public PrimMST(EdgeWeightedGraph G) {
        edgeTo = new Edge[G.V()];
        distTo = new double[G.V()];
        marked = new boolean[G.V()];
        pq = new PriorityQueue<>();
        weight = 0.0;
        // 初始化所有权重为无限大
        for (int v = 0; v < G.V(); v++)
            distTo[v] = Double.POSITIVE_INFINITY;

        // 逐个顶点扫描，计算最小生成树
        for (int v = 0; v < G.V(); v++)
            if (!marked[v]) prim(G, v);
    }
    
    private void prim(EdgeWeightedGraph G, int s){
        distTo[s] = 0.0;
        // 扫描顶点
        scan(G, s);

        while (!pq.isEmpty()){
            // 循环取出最小键，即权重最小的横切边，
            // 这条边一定属于最小生成树
            Edge e = pq.poll();
            int v = e.either(), w = e.other(v); 
            weight += e.weight();
            // 扫描横切边的另外一个顶点
            if (marked[v]) scan(G, w);
            else scan(G, v);
        }
    }

    private void scan(EdgeWeightedGraph G, int v) {
        // 标记当前顶点为已扫描
        marked[v] = true;
        // 遍历邻接边，找出最小权重横切边
        for (Edge e : G.adj(v)) {
            int w = e.other(v);
            // 如果已经扫描过，则继续遍历其他邻接点
            if (marked[w]) continue;

            // 如果当前横切边比记录的横切边权重小
            // 则更新横切边及其权重
            if (e.weight() < distTo[w]) {
                // 更新权重
                distTo[w] = e.weight();
                // 如果优先队列中包含失效边，则删除
                if (pq.contains(edgeTo[w])){
                    pq.remove(edgeTo[w]);
                }
                // 更新横切边
                edgeTo[w] = e;
                // 这条横切边加入优先队列
                pq.offer(edgeTo[w]);
            }
        }
    }
}

参考代码：PrimMST

特点

优先队列记录非树顶点到树中的最小权重横切边，堆顶的最小权重横切边满足切分定理，而这条边的非树顶点就是下一个被添加到树中的顶点。

延时实现和即时实现差别

延时实现

• 优先队列
  优先队列中存储了图中所有的边！取出权值最小的边，再判断是否为横切边（即边的两个顶点只有一个被扫描过）。
• 时间复杂度
  优先队列存储了所有边即 E 条边，插入和删除的时间复杂度都为 logE，而 while 循环中遍历这 E 条边，所以总的复杂度为 O(ElogE) 。

即时实现

• 优先队列
  优先队列中只存储非树顶点到树中的最小权重横切边！堆顶的最小权重横切边满足切分定理，也就是这条边必然属于最小生成树。
• 时间复杂度
  优先队列始终最多存储了 V 个顶点最小生成树的边，即 V 条边。插入和删除的时间复杂度都为 logV，遍历 E 条边，所以总的复杂度为 O(ElogV) 。

小结

• 两种实现都没有考虑图的连通性。如果为非连通图，会输出所有的极大连通子图的最小生成树

参考文档

• 《算法：第四版》 第 4 章
• algs4: mst
• 百科：Prim 算法
• visualgo动画-Prim延时实现
• usfca动画-Prim即时实现
• Prim算法详解