算法 - 最小生成树 Kruskal 算法

Kruskal 算法 - 克鲁斯卡尔算法，是一种用来寻找最小生成树的算法。在剩下的所有未选取的边中，找最小边；如果和已选取的边构成回路，则放弃选取次小边。

概念

最小生成树 MST: Minimum Spanning Tree ：也是最小权重生成树的简称。一幅加权无向图，包含所有顶点的无环连通子图，该子图中所有边（ V-1 条边）的权值之和最小。

算法定义

Kruskal 算法的主要思想是按照边的权重顺序（从小到大）处理它们，将边加入最小生成树中，加入的边不会与已经加入的边构成环，直到树中含有 V-1 条边为止。

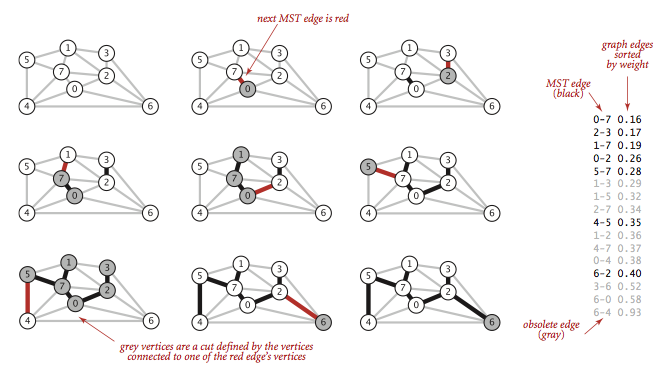
动画演示

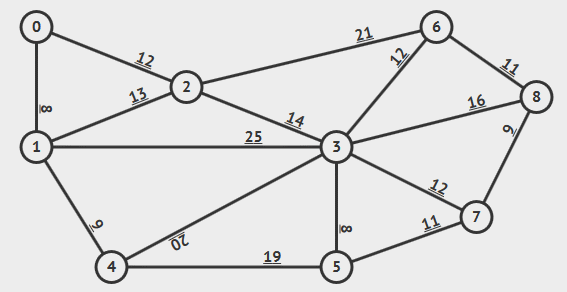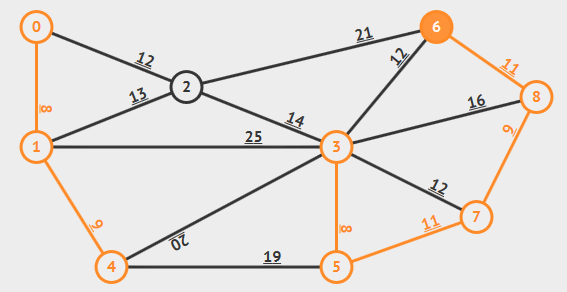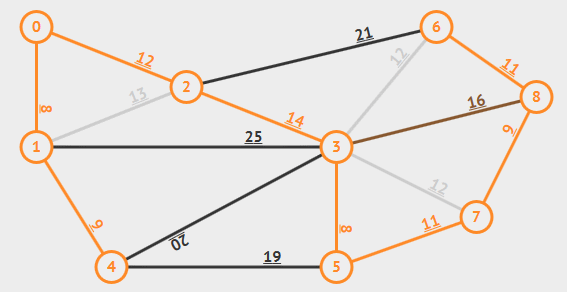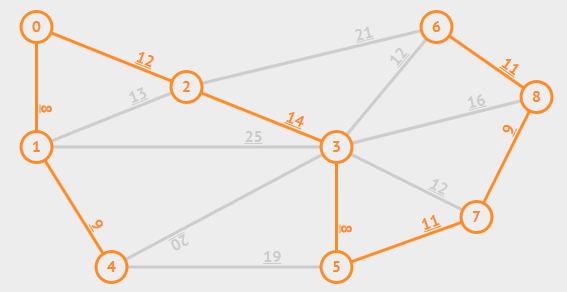
算法解析

weight
记录最小生成树的总权重。
Queue<Edge> mst 队列
记录最小生成树中所有的边。
MinPQ<Edge> pq 最小优先队列
小根堆，加入所有边，堆顶为权重最小的边。
UF uf 并查集
判断无向图中两个顶点的连通性。

算法实现非常简单：

将所有边加入最小优先队列，确保堆顶都是最小权重边
根据顶点个数建立并查集
小根堆取出堆顶元素，如果边两端的顶点不连通，根据 Kruskal 算法定义，将边加入最小生成树 mst 队列中；如果两个顶点连通，则忽略这条边
直到小根堆所有边取出或者达到 V-1 条边，最小生成树完成

public class KruskalMST {
    private double weight;                        // weight of MST
    private Queue<Edge> mst = new Queue<Edge>();  // edges in MST

    public KruskalMST(EdgeWeightedGraph G) {
        // more efficient to build heap by passing array of edges
        MinPQ<Edge> pq = new MinPQ<Edge>();
        for (Edge e : G.edges()) {
            pq.insert(e);
        }

        // run greedy algorithm
        UF uf = new UF(G.V());
        while (!pq.isEmpty() && mst.size() < G.V() - 1) {
            Edge e = pq.delMin();
            int v = e.either();
            int w = e.other(v);
            if (!uf.connected(v, w)) { // v-w does not create a cycle
                uf.union(v, w);  // merge v and w components
                mst.enqueue(e);  // add edge e to mst
                weight += e.weight();
            }
        }
    }
}