算法 - 最短路径树 Bellman-Ford 算法

Bellman-Ford 贝尔曼-福特算法，是求含负权图的单源最短路径的一种算法。特点：支持有环，负权重，但不能存在负权重环。

最短路径树及边的松弛，相关概念见《算法 - 最短路径树以及 Dijkstra 算法》。

算法定义

Bellman-Ford 算法：在任意含有 V 个顶点的加权有向图中给定起点 s，从 s 无法到达任何负权重环，以下算法能够解决其中的单点最短路径问题：
将 distTo[s] 初始化为 0，其他 distTo[] 元素初始化为无穷大，以任意顺序放松有向图的所有边，重复 V 轮。算法证明如下：

算法实现

// 重复 V 轮
for(int pass = 0; pass < G.V(); pass++)
    // 两个 for 找出 E 条边
    for (v = 0; v < G.V(); v++)
        for (DirectedEdge e : G.adj(v))
            relax(e);

根据算法定义和实现可以看出，Bellman-Ford 算法需要重复 V 轮，每一轮都会对所有边（E 条边）进行放松，时间复杂度总是为 O(EV) 。具体步骤看下面动画：

动画演示

负权重边
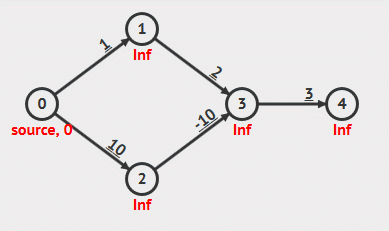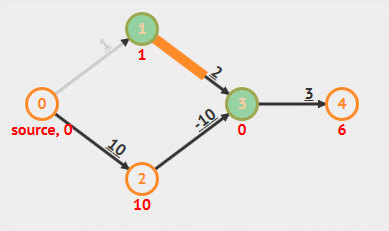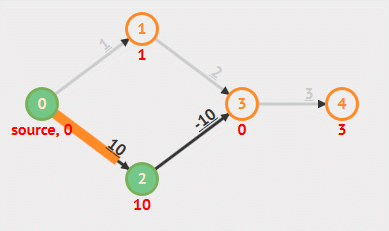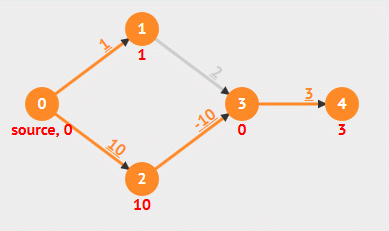
负权重环

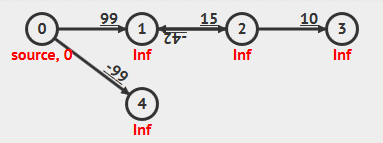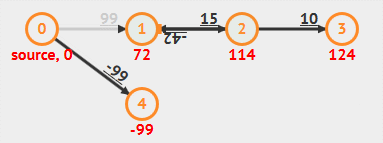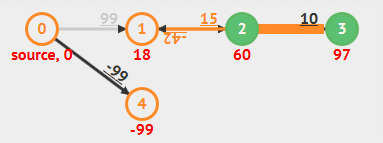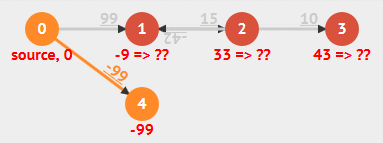
基于队列对算法改进

在 Bellman-Ford 算法的执行过程中，很容易发现任意一轮中，很多边的放松都不成功：只有上一轮中的 distTo[] 值发生变化的顶点指出的边，才能改变其他 distTo[] 元素的值（可以参考负权重环算法执行动画）。
SPFA: Shortest Path Faster Algorithm 是 Bellman-Ford 算法的一种队列优化。使用一条 FIFO 队列记录这样的顶点：放松边的顺序是出队顺序；当 distTo[w] 值发生变化的顶点进入队列，即放松生效时的顶点入队。

算法轨迹

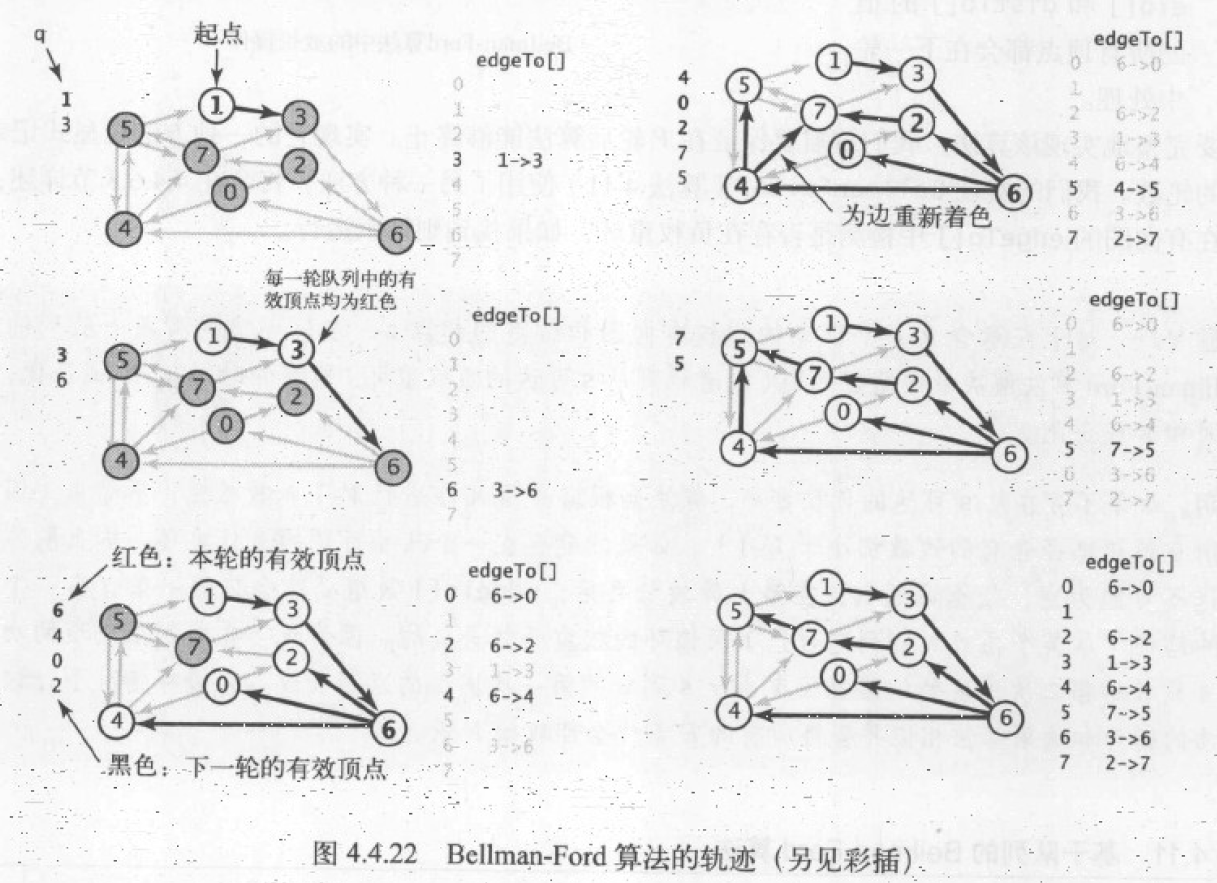
算法实现

Queue<Integer> queue 队列
一条保存即将被放松的顶点的队列。
boolean[] onQueue 数组
用来指示顶点是否已经在队列中存在，防止将顶点重复插入队列。
double[] distTo 数组
记录起点到当前顶点的，最短路径估计长度。
DirectedEdge[] edgeTo 数组
记录起点到当前顶点最短路径上，最后一条边。也就是说前驱顶点到当前顶点的边。

public BellmanFordSP(EdgeWeightedDigraph G, int s) {
    distTo  = new double[G.V()];
    edgeTo  = new DirectedEdge[G.V()];
    onQueue = new boolean[G.V()];
    // 初始化
    for (int v = 0; v < G.V(); v++)
        distTo[v] = Double.POSITIVE_INFINITY;
    distTo[s] = 0.0;
    
    // Bellman-Ford algorithm
    queue = new Queue<Integer>();
    queue.enqueue(s);
    onQueue[s] = true;
    while (!queue.isEmpty() && !hasNegativeCycle()) {
        int v = queue.dequeue();
        onQueue[v] = false;
        relax(G, v);
    }
}

private void relax(EdgeWeightedDigraph G, int v) {
    for (DirectedEdge e : G.adj(v)) {
        int w = e.to();
        if (distTo[w] > distTo[v] + e.weight()) {
            distTo[w] = distTo[v] + e.weight();
            edgeTo[w] = e;
            // distTo[w] 发生变化，将对应顶点入队
            // 入队前先判断是否已经在队列中存在
            if (!onQueue[w]) {
                queue.enqueue(w);
                onQueue[w] = true;
            }
        }
        // 放松 V 轮后，检测是否存在环
        // 如果存在，则一定是负权重环
        if (cost++ % G.V() == 0) {
            findNegativeCycle();
            if (hasNegativeCycle()) return;  // found a negative cycle
        }
    }
}

// by finding a cycle in predecessor graph
private void findNegativeCycle() {
    int V = edgeTo.length;
    EdgeWeightedDigraph spt = new EdgeWeightedDigraph(V);
    // 边构造的有向图，环检测
    for (int v = 0; v < V; v++)
        if (edgeTo[v] != null)
            spt.addEdge(edgeTo[v]);

    EdgeWeightedDirectedCycle finder = new EdgeWeightedDirectedCycle(spt);
    cycle = finder.cycle();
}

根据算法分析，每个顶点都会至少入队一次，即会放松 E 条边；但是每个顶点在出队被放松后，会存在重复入队的情况（这正是和广度优先搜索最大的区别，广度优先搜索每个顶点只入队一次）；也就是说在最坏情况下可能会重复入队 V 次，所以最坏时间复杂度还是 O(EV)。通常情况下，SPFA 算法效率会比常规的 Bellman-Ford 算法快。

负权重环转换

Bellman-Ford 算法对负权重环检测，转换为仅仅需要检测是否存在环的原理：
将所有边放松 V 轮后，当且仅当队列非空时，有向图中才存在从起点可达的负权重环，因此 edgeTo[] 数组所表示的子图中必然含有这个负权重环。所以负权重环的检测，可以转化为 edgeTo[] 中的边构造的有向图，并检测该图是否存在环。

小结

权重
边的权重可以为负值，但不能包含负权重环，有向图中可以有环。
边的放松顺序
原始 Bellman-Ford 算法：以任意顺序放松边，放松 V 轮；SPFA 基于队列改进型算法：当 distTo[w] 值发生变化的顶点进入队列，以 FIFO 的方式放松该顶点指向邻接点的边。
时间复杂度
不管是 Bellman-Ford 算法，还是基于队列改进后的算法 SPFA，最坏情况下的时间复杂度都是 O(EV) 。

算法定义

算法实现

动画演示

基于队列对算法改进

算法轨迹

算法实现

负权重环转换

小结

参考文档