算法 - 最短路径应用场景

发表于 | 分类于 | 阅读次数

最短路径常见应用场景：加权无向图最短路径、给定两点的最短路径、加权有向无环图的最长路径、并行任务调度、负权重环检测、套汇等等。

加权无向图最短路径

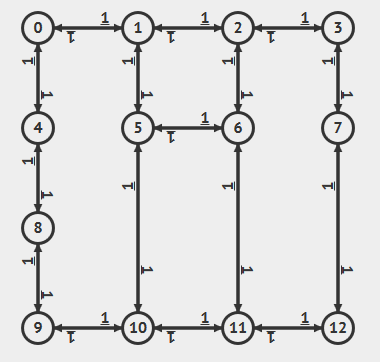
将无向图看成有向图，利用有向图的算法来计算最短路径。

  • 转换
    给定的加权无向图，创建一幅由相同顶点构成的加权有向图，且对于无向图中的每条边，相应地创建两条（方向不同）有向边。有向图中的路径和无向图中的路径存在一一对应的关系，路径的权重也是相同的；所以最短路径问题是等价的。
  • 特点
    权值不能为负值，否则在创建对应有向图时，每两个顶点间都存在一个负权重环。

0101-spt-samples-weight-graph.png

给定两点的最短路径

给定一幅加权有向图，以及一个起点 s 和一个终点 t ，找到 s 到 t 的最短路径。
如果不包含负权重，可以在 Dijkstra 算法中，从优先队列取出目标顶点 t 之后终止搜索，而 distTo[t] 则为最短路径值。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public DijkstraSP(EdgeWeightedDigraph G, int s) {
    ...

    // relax vertices in order of distance from s
    pq = new IndexMinPQ<Double>(G.V());
    pq.insert(s, distTo[s]);
    while (!pq.isEmpty()) {
        int v = pq.delMin();
        // 如果 v 为终点，则跳出循环，计算结束
        if (v == endVertex) break;
        for (DirectedEdge e : G.adj(v))
            relax(e);
    }
    ...
}

加权有向无环图的最长路径

给定一幅无环加权有向图和起点 s，是否存在一条 s 到给定顶点 v 的路径？找出最长（总权重最大）的路径。

算法一：转换为最短路径

复制原始无环加权有向图得到一个副本，并将副本中所有边的权重变为负值。计算副本中的最短路径，即为原图中的最长路径。

算法二：修改最短路径判断条件

修改最短路径算法，初始化时将 distTo[] 为负无穷，放松边时判断 distTo[w] < distTo[v] + e.weight() ，这样就称为最长路径算法了。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
public AcyclicLP(EdgeWeightedDigraph G, int s) {
    distTo = new double[G.V()];
    edgeTo = new DirectedEdge[G.V()];

    validateVertex(s);

    // 初始化为负无穷
    for (int v = 0; v < G.V(); v++)
        distTo[v] = Double.NEGATIVE_INFINITY;
    distTo[s] = 0.0;

    // relax vertices in topological order
    Topological topological = new Topological(G);
    if (!topological.hasOrder())
        throw new IllegalArgumentException("Digraph is not acyclic.");
    for (int v : topological.order()) {
        for (DirectedEdge e : G.adj(v))
            relax(e);
    }
}

// relax edge e, but update if you find a *longer* path
private void relax(DirectedEdge e) {
    int v = e.from(), w = e.to();
    // 放松时，改为小于
    if (distTo[w] < distTo[v] + e.weight()) {
        distTo[w] = distTo[v] + e.weight();
        edgeTo[w] = e;
    }       
}

并行任务调度

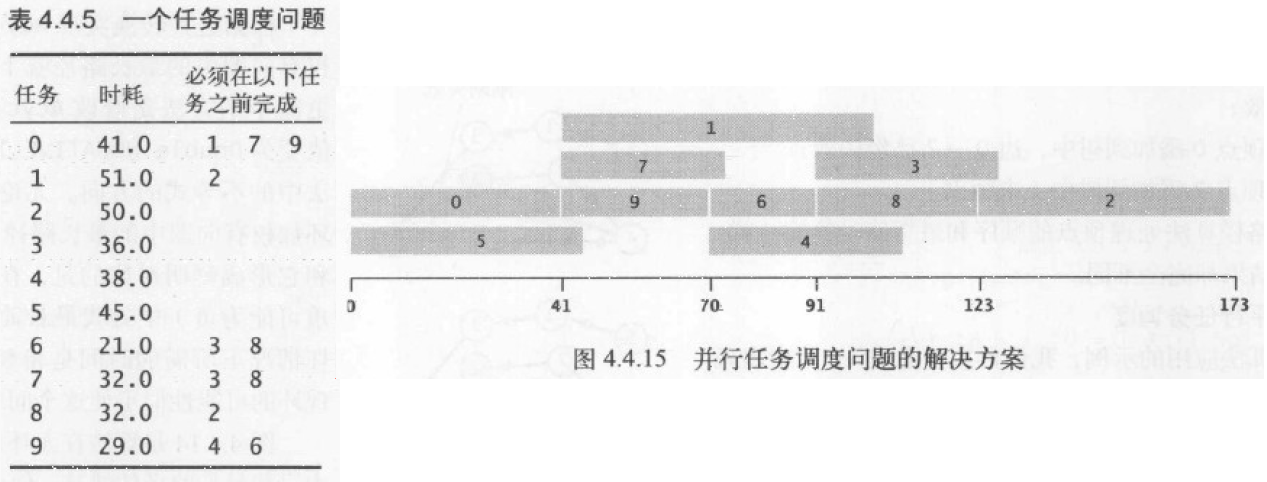
优先级限制下的并行任务调度：给定一组需要完成的特定任务，以及一组关于任务完成的先后次序的优先级限制！在满足限制条件的前提下，应该如何在若干相同处理器上安排任务，并在最短时间内完成所有任务？
关键路径：并行任务序列中，耗时最长路径即为关键路径。可以证明：关键路径和无环加权有向图的最长路径问题是等价的。

0101-spt-samples-parallel-tasks-scheduling.png

解决关键路径步骤

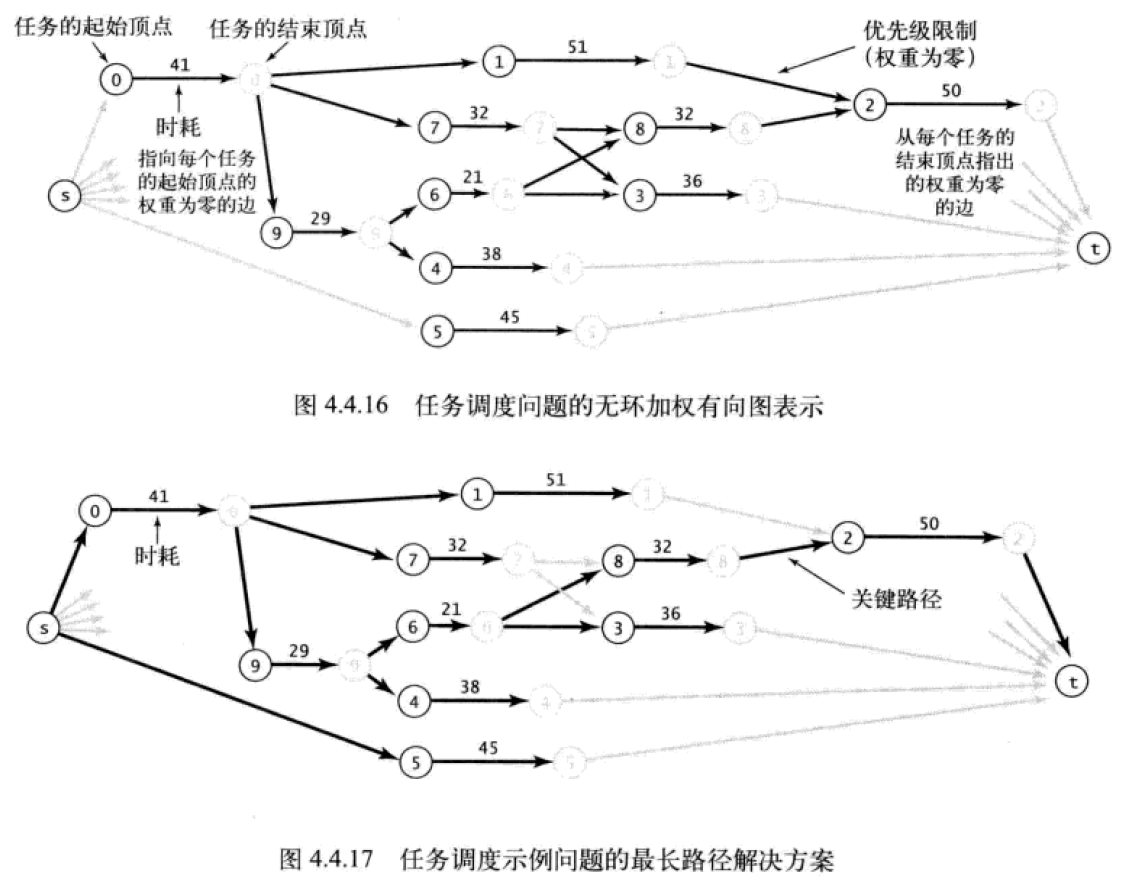
解决并行任务调度的关键路径的方法步骤如下：

  • 创建一幅无环加权有向图，其中包含起点 s 和终点 t，并且每个任务都对应两个顶点（任务起始顶点和任务结束顶点）。也就是说 N 个任务的无环加权有向图中，一共有 2*N+2 个顶点。其中 2*N 表示为图的起点，2*N+1 为图的终点，i 为任务起始顶点，i+N 为任务的结束顶点
  • 每个任务都有一条从它的起始顶点到结束顶点的边，边的权重即为任务所需时间
  • 对于每条优先级限制 v-w，添加一条从 v 的结束顶点指向 w 的起始顶点的边，并设定权重为零
  • 为每个任务添加一条从图的起点 s 指向任务的起始顶点的边，并设定权重为零
  • 为每个任务添加一条从任务的结束顶点指向图的终点 t 的边，并设定权重为零
  • 这样每个任务预计的开始时间：为图的起点 s 到任务的起始顶点的最长距离
  • 并行任务调度的关键路径为：图的起点 s 到图的终点 t 的最长距离

并行任务调度转换为：无环加权有向图的最长路径。

0101-spt-samples-dag-critical-path.png

测试数据

并行任务调度数据： 

1
2
3
4
5
6
7
8
9
10
11
12
13
$ more jobPC.txt
10
//耗时 共有几个前置任务 前置任务列表
41.0  3  1 7 9
51.0  1  2
50.0  0
36.0  0
38.0  0
45.0  0
21.0  2  3 8
32.0  2  3 8
32.0  1  2
29.0  2  4 6

测试数据共有 10 个任务，其中第七行数据 21.0 2 3 8 表示：任务 7 的耗时为 21.0，有 2 个前置任务；任务 7 必须在任务 3,8 两个前置任务之前完成。数据对应的是上面的示例图。

算法分析

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
public class CPM {

    // this class cannot be instantiated
    private CPM() { }
    public static void main(String[] args) {
        // 给定任务数
        int n = StdIn.readInt();
        
        // 图的起点 s，终点 t
        int s = 2*n;
        int t = 2*n + 1;
        
        // 创建无环加权有向图，顶点供 2*n+2 个
        EdgeWeightedDigraph G = new EdgeWeightedDigraph(2*n + 2);
        for (int i = 0; i < n; i++) {
            // 任务耗时
            double duration = StdIn.readDouble();
            // 为每个任务添加一条从图的起点 s 指向任务的起始顶点的边
            // 并设定权重为零  
            G.addEdge(new DirectedEdge(s, i, 0.0));
            // 为每个任务添加一条从任务的结束顶点指向图的终点 t 的边
            // 并设定权重为零  
            G.addEdge(new DirectedEdge(i+n, t, 0.0));
            // 每个任务都有一条从它的起始顶点到结束顶点的边
            // 边的权重即为任务所需时间
            // 其中 i 为任务的起始顶点，i+n 为任务的结束顶点
            G.addEdge(new DirectedEdge(i, i+n,    duration));
        
            // precedence constraints
            // 前置任务个数
            int m = StdIn.readInt();
            for (int j = 0; j < m; j++) {
                // 前置任务，对于每条优先级限制 v-w，
                // 添加一条从 v 的结束顶点指向 w 的起始顶点的边，并设定权重为零
                int precedent = StdIn.readInt();
                G.addEdge(new DirectedEdge(n+i, precedent, 0.0));
            }
        }
    
        // compute longest path
        // 计算加权有向无环图的最长路径
        AcyclicLP lp = new AcyclicLP(G, s);
        
        // print results
        StdOut.println(" job   start  finish");
        StdOut.println("--------------------");
        for (int i = 0; i < n; i++) {
            StdOut.printf("%4d %7.1f %7.1f\n", 
                i, lp.distTo(i), lp.distTo(i+n));
        }
        StdOut.printf("Finish time: %7.1f\n", lp.distTo(sink));
    }
}

测试结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
% java CPM < jobsPC.txt
 job   start  finish
--------------------
   0     0.0    41.0
   1    41.0    92.0
   2   123.0   173.0
   3    91.0   127.0
   4    70.0   108.0
   5     0.0    45.0
   6    70.0    91.0
   7    41.0    73.0
   8    91.0   123.0
   9    41.0    70.0
Finish time:   173.0

负权重环检测

Bellman-Ford 算法包含了负权重环的检测，可以使用该算法来计算最短路径并判断是否存在负权重环。

套汇

套汇问题等价于加权有向图中的负权重环的检测问题。

转换步骤

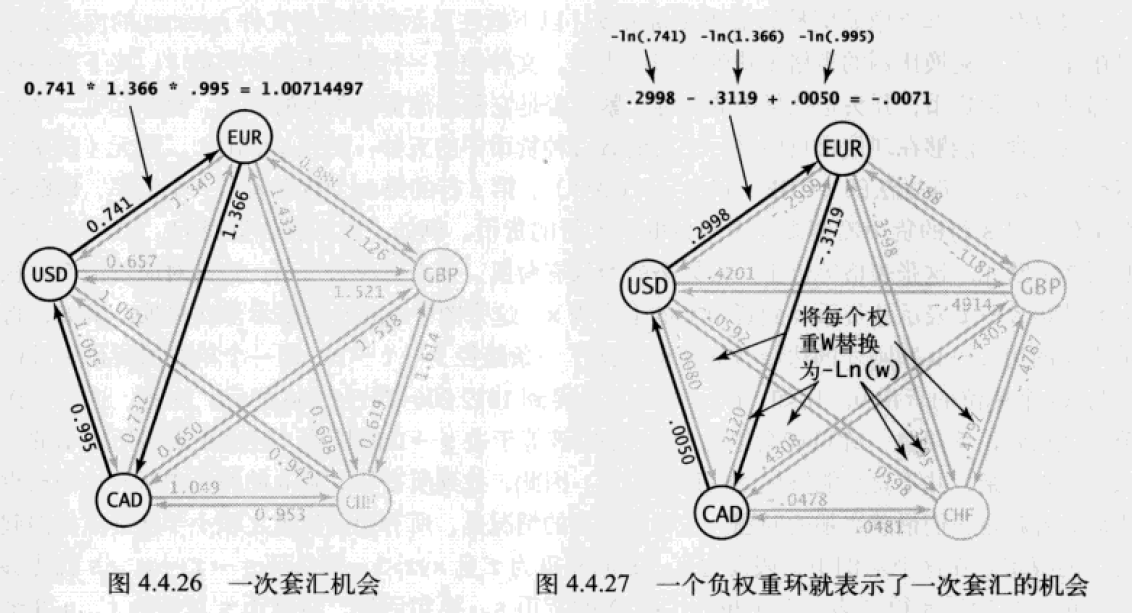
取每条边权重的自然对数并取反，这样套汇问题中的权重之积的计算转换为新图中的所有边权重之和的计算。任意权重之积 w1*w2*...wk 即对应 -lnw1-lnw2...-lnwk 之和。转换后边的权重可能为正也可能为负，一条从 v 到 w 的路径表示将货币 v 兑换为货币 w，任意负权重环都是一次套汇机会。

0101-spt-samples-arbitrage-detection.png

测试数据

套汇测试数据各种货币汇率： 

1
2
3
4
5
6
7
% more rates.txt
5
USD 1      0.741  0.657  1.061  1.005
EUR 1.349  1      0.888  1.433  1.366
GBP 1.521  1.126  1      1.614  1.538
CHF 0.942  0.698  0.619  1      0.953
CAD 0.995  0.732  0.650  1.049  1

第一行数据 USD 1 0.741 0.657 1.061 1.005 表示：当前顶点代表美元 USD ，兑换其他四种货币的汇率分别为 0.741 0.657 1.061 1.005 。

算法解析

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
public class Arbitrage {

    // this class cannot be instantiated
    private Arbitrage() { }

    public static void main(String[] args) {

        // V currencies
        // 读取一共有几种货币
        int V = StdIn.readInt();
        String[] name = new String[V];

        // create complete network
        // 创建加权有向图
        EdgeWeightedDigraph G = new EdgeWeightedDigraph(V);
        for (int v = 0; v < V; v++) {
            // 货币名称
            name[v] = StdIn.readString();
            for (int w = 0; w < V; w++) {
                // 兑换其他货币汇率
                double rate = StdIn.readDouble();
                DirectedEdge e = new DirectedEdge(v, w, -Math.log(rate));
                G.addEdge(e);
            }
        }

        // find negative cycle
        // 使用 Bellman-Ford 算法，判断是否存在负权重环
        BellmanFordSP spt = new BellmanFordSP(G, 0);
        if (spt.hasNegativeCycle()) {
            double stake = 1000.0;
            // 如果存在，找出负权重环路径
            for (DirectedEdge e : spt.negativeCycle()) {
                StdOut.printf("%10.5f %s ", stake, name[e.from()]);
                stake *= Math.exp(-e.weight());
                StdOut.printf("= %10.5f %s\n", stake, name[e.to()]);
            }
        }
        else {
            StdOut.println("No arbitrage opportunity");
        }
    }

}

测试结果

1
2
3
4
% java Arbitrage < rates.txt
1000.00000 USD =  741.00000 EUR
 741.00000 EUR = 1012.20600 CAD
1012.20600 CAD = 1007.14497 USD

表示存在负权重环，有套现机会。套现路径为：USD -> EUR -> CAD -> USD，即 1000 美元经过套汇后，能获取 1007 美元。

参考文档

  • 《算法：第四版》 第 4 章
0%