算法 - 子字符串匹配 BM 算法

发表于 | 分类于 | 阅读次数

介绍子字符串匹配算法：从右至左暴力匹配算法，BM 算法。

从右至左暴力匹配算法

算法实现

使用下标 j 记录文本位置；使用下标 i 记录模式位置。从模式最右边的字符开始比较，从右向左直到整个模式匹配，则返回文本位置。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
private int bruteForce(String pattern, String text){
    int m = pattern.length();
    int n = text.length();

    int j = 0;              // 记录文本当前比较位置
    int i = m - 1;          // 记录模式当前比较位置

    while (j <= n - m && i >= 0){
        // 模式从右向左和文本匹配
        // 如果匹配，模式向左缩进一位继续比较
        if (pattern.charAt(i) == text.charAt(i + j)) {
            i--;
        } else {
            // 如果不匹配，文本向右移动一位
            // i 恢复为在模式最右边
            j++;
            i = m - 1;
        }
    }

    if (i < 0) return j;
    return n;
}

时间复杂度

暴力匹配算法在长度为 N 的文本中查找长度为 M 的模式，时间复杂度为 O(NM) 。

BM 算法基础概念

BM: Boyer-Moore 算法：大部分文本编辑器的查找功能 CTRL+F ，都是使用的该算法。KMP 算法中，模式和文本同时向右移动，文本逐个字符向后移动（不回退），模式从左向右逐个字符去匹配，当出现不匹配时，模式可以利用已知信息向前跳跃式继续匹配。而 BM 算法中，文本跳跃式向后移动，模式从右向左逐个字符匹配（这会变相导致文本出现回退），当出现字符不匹配时，利用模式的已知信息，文本可以直接大范围跳跃式向后移动，这也是算法更高效的原因。
BM 算法中计算的是文本的移动距离，它会依据坏字符和好字符规则来决定；而 KMP 算法计算的是模式的移动距离。

坏字符规则

坏字符 bad character：模式与文本匹配过程中，文本出现的第一个不匹配字符。也就是坏字符是文本中的字符。

0103-strings-search-bm-bad-character.png

示例中：S 即为坏字符，不匹配的字符。

坏字符规则移动位数

移动位数：坏字符位置 - 模式中上一次出现的位置

位置是从 0 开始编号的；如果坏字符不在模式中，则上次出现位置为 -1 。

  • 坏字符不在模式中
    文本向右移动位数：坏字符及前面字符串的长度；即坏字符所在位置加上 1 。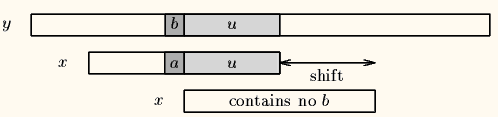
    0103-strings-search-bm-bad-character-case-1.png
  • 坏字符在模式中
    文本向右移动位数：坏字符位置 - 模式中上一次出现的位置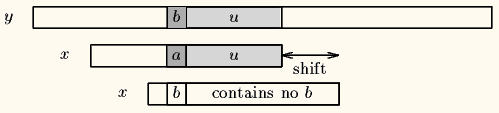
    0103-strings-search-bm-bad-character-case-2.png
  • 示例
    模式从尾部开始和文本比较：文本中 P 与模式最后一个字符 E 不匹配，坏字符 P 的位置为 6 ，而它在模式中上一次出现的位置为 4 ，所以坏字符规则移动位数为：6-4=2 。
    0103-strings-search-bm-bad-character-2.png

好后缀规则

好后缀 good suffix：模式与文本匹配过程中，模式已经与文本相匹配了的字符串。也就是模式中所有尾部匹配的字符串。

0103-strings-search-bm-good-suffix.png

示例中：模式尾部匹配的字符串为 MPLE, PLE, LE, E，它们都是好后缀，而 MPLE 为最长好后缀。

好后缀规则移动位数

好后缀匹配有三种情况：

  • case1 模式串中有子串和最长好后缀完全匹配，则将最靠右的那个子串（最长好后缀在模式中上一次出现位置的子串）移动到好后缀的位置继续进行匹配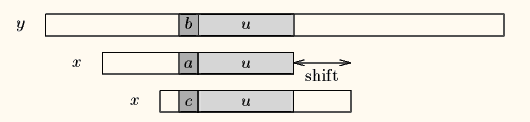
    0103-strings-search-bm-good-suffix-case-1.png
  • case2 如果不存在和最长好后缀完全匹配的子串，则在好后缀中找到 pattern[m-1-s…m-1]=pattern[0…s] 尽量长并匹配的子串，也就是从模式第一个字符开始匹配的子串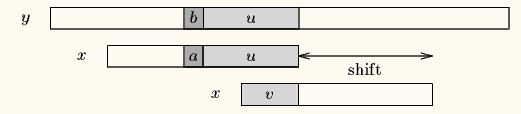
    0103-strings-search-bm-good-suffix-case-2.png
  • case3 如果完全不存在和好后缀匹配的子串，则右移模式长度的距离

移动位数：好后缀位置 - 模式中上一次出现的位置

  • 好后缀的位置
    以最后一个字符位置为准。也就是说，好后缀位置其实始终为 m-1 ，m 为模式长度。
  • 模式中上一次出现的位置
    根据上面三种匹配规则：当存在和最长好后缀完全匹配的子串时，上一次出现位置为子串位置；当好后缀只有部分子串匹配时，需要找到从头部开始匹配的尽量长的好后缀子串，上一次出现位置为该子串的位置；如果不存在和好后缀匹配的子串，上一次出现位置为 -1 。
    因为模式是从右向左匹配的，所以这里说的子串位置，指的是子串最右边字符的位置。
  • 示例
    上面好后缀规则示例中 MPLE, PLE, LE, E 都是好后缀，以最后一个字符 E 为准，好后缀位置为 6 。因为好后缀只有部分子串匹配，从头部开始匹配尽量长的好后缀子串为 E，它在模式中上一次出现的位置为 0 ，所以好后缀规则移动位数为 6-0=6 。

文本移动位数

BM 算法的基本思想，文本的最终移动位置为两个规则移动位数的最大值。

文本移动位数 = Max{坏字符规则移动位数，好后缀规则移动位数} 。

图解

示例文本：HERE IS A SIMPLE EXAMPLE；模式 EXAMPLE 。

0103-strings-search-bm-examples.png

BM 算法解析

坏字符距离数组 bmBc[]

数组相关信息：

  • 数组长度
    通常以 8 位字符也就是 256 位长度来表示所有字符，也就是 ASCII 能表示的字符；如果是模式中存在中文，需要使用 16 为字符也就是 65536 位长度来表示。大部分算法中都取的是 256 （可能因为算法主要针对的是英文吧？）。
  • 下标
    以字符作为下标，而不是位置。这就是为什么要用 256 来表示数组长度了，数组可以包含所有的 ASCII 字符。
  • 含义
    bmBc['v'] 表示字符 v 在模式中最后一次出现的位置，距离模式尾部的长度。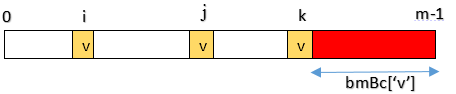
    0103-strings-search-bm-bad-character-array.png

在坏字符规则中，对应两种情况，我们分别计算对应的坏字符数组：

  • 坏字符没有出现在模式中
    这种情况很简单，坏字符在模式中上一次出现的位置为 -1，所以距离模式尾部为模式的长度：bmBc['v'] = pattern.length() 。
  • 坏字符出现在模式中
    如果坏字符上一次出现的位置为 i ，那么坏字符距离模式尾部的距离为：bmBc['v'] = pattern.length()-i-1 。

坏字符规则移动位数

坏字符数组 bmBc[] 表示：坏字符最后一次出现位置距离模式尾部的长度。我们根据这个长度来计算坏字符规则中，模式的移动位数：

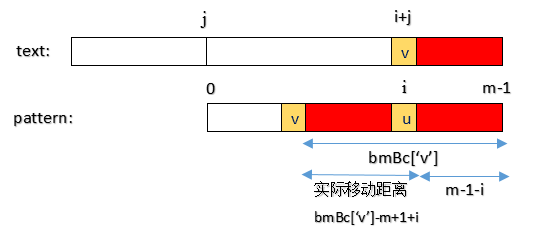
0103-strings-search-bm-bad-character-array-shift.png

模式在第 i 个位置的字符 u，和文本在第 i+j 个位置的字符 v 不匹配，坏字符为 v。坏字符在模式中上一次出现，距离模式尾部的距离为 bmBc['v']，所以坏字符在模式中上一次出现的位置为 m-1-bmBc['v']。
套用公式：模式实际移动位数 = 坏字符位置 - 模式中上一次出现的位置。模式实际移动位数为 i - (m-1-bmBc['v'])，即 bmBc['v']-m+1+i 。

好后缀长度数组 suffix[]

好后缀长度数组 suffix[] 长度等于模式的长度，它的下标就是位置。模式以最后一个字符为准，对应的所有后缀中，suffix[i] 表示以 i 位置结束的子串，其所有后缀中和模式所有后缀的最长共有元素长度。
根据以上定义，假设模式为 bcababab ，它对应的所有后缀为 bcababab, cababab, ababab, babab, abab, bab, ab, b ，从右向左计算模式的每个子串的所有后缀和模式所有后缀的最长共有元素长度：

模式的子串 子串的所有后缀 最长共有元素 长度
bcababab bcababab, cababab, ababab, babab, abab, bab, ab, b bcababab 8
bcababa bcababa, cababa, ababa, baba, aba, ba, a 无 0
bcabab bcabab, cabab, abab, bab, ab, b abab 4
bcaba bcaba, caba, aba, ba, a 无 0
bcab bcab, cab, ab, b ab 2
bca bca, ca, a 无 0
bc bc, c 无 0
b b b 1

有了以上定义和示例说明，通过算法来计算 suffix[] 数组，假设：

  • i 是当前位置，计算 suffix[i] 的值
  • f 是上一轮匹配成功的起始位置
  • g 是上一轮匹配的失配位置

这里的匹配指的是 i 位置的子串与模式后缀的匹配。从右向左扫描模式，也就是从后向前计算 suffix[] 数组：

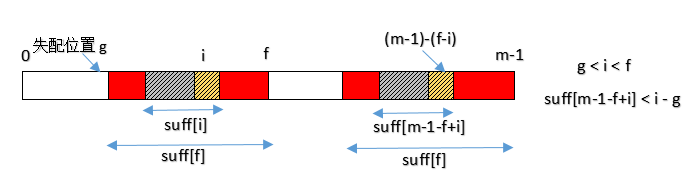
0103-strings-search-bm-suffix-array.png

当 g < i < f 时，必定会有 pattern[i]=pattern[m-1-f+i] ；如果 suffix[m-1-f+i] < i-g ，则必定会有 suffix[i] = suffix[m-1-f+i] ，充分利用已经计算过的 suffix 值。
如果是其他情况（即不能利用已知的 suffix 值），也就是说并不是每个位置都能进行成功匹配（实际上能够进行成功匹配的位置并不多）。当在起始位置就不匹配时，可以假定 f=g=i ，直接逐个字符比较计算 suffix 值。

好后缀移位数组 bmGs[]

好后缀移位数组 bmGs[] 长度：等于模式的长度，它的下标就是位置，它的计算需要借助好后缀长度数组 suffix[] 。

  • case1 模式中有子串和最长好后缀完全匹配
    位置 j 出现不匹配，移动位数为 bmGs[j]=m-1-i，即 bmGs[m-1-suffix[i]]=m-1-i 。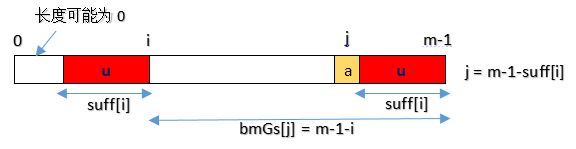
    0103-strings-search-bm-good-suffix-array-case-1.png
  • case2 模式中没有最长好后缀的子串，则在好后缀中找到 pattern[m-1-s…m-1]=pattern[0…s] 尽量长并匹配的子串
    位置 j 出现不匹配，当 0<=j<m-1-i 时，存在 suffix[i]=i+1 ，且移动位数为 bmGs[j]=m-1-i 。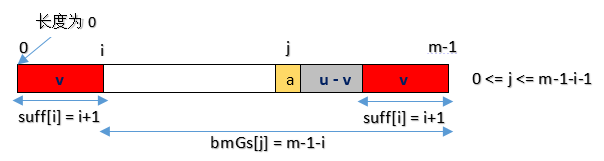
    0103-strings-search-bm-good-suffix-array-case-2.png
  • case3 完全不存在和好后缀匹配的子串
    只要出现不匹配，移动位数为整个模式长度，即 bmGs[i]=m 。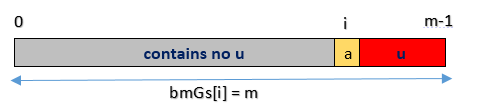
    0103-strings-search-bm-good-suffix-array-case-3.png

算法实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
public class BoyerMoore {
    private final int R;     // the radix
    
    public BoyerMoore(){
        this.R = 256;
    }

    private int bmBc[];
    private int suffix[];
    private int bmGs[];

    private void preBmBc(String pattern){
        // 坏字符距离数组，用 256 来表示数组长度了，包含所有的 ASCII 字符
        bmBc = new int[R];
        int m = pattern.length();

        // 坏字符没有出现在模式中 
        for (int i = 0; i < R; i++)
            bmBc[i] = m;

        // 坏字符存在模式中  
        for (int i = 0; i < m - 1; i++)
            bmBc[pattern.charAt(i)] = m - i - 1;
    }
    
    private void preSuffix(String pattern){
        int m = pattern.length();
        // suffix 数组长度为模式长度
        suffix = new int[m];

        // 从右向左扫描
        int i = m - 1;
        int f = i, g = i;

        // 最后一个元素就是模式本身，所以长度为 m 
        suffix[m - 1] = m;
        // 从倒数第二个字符开始
        for (i = m - 2; i >= 0; i--) {
            // 如果满足假设条件，利用已经计算过的 suffix 值
            if (i > g && suffix[i + m - 1 - f] < i - g)
                suffix[i] = suffix[i + m - 1 - f];
            else {
            // 否则逐个字符比较
                // f 记录上一轮匹配成功的起始位置
                f = g = i;
                // g 在第 i 个位置，从右向左移动，直到出现不匹配
                // g 同时记录上一轮匹配失配位置
                while (g >= 0 && pattern.charAt(g) == 
                        pattern.charAt(m - 1 - i + g))
                    g--;
                // 第 i 个位置的公共好后缀长度为 i - g
                suffix[i] = i - g;
            }
        }
    }

    private void preBmGs(String pattern){
        preSuffix(pattern);
        int m = pattern.length();
        bmGs = new int[m];

        // case3: 模式中完全不存在和好后缀匹配的子串  
        for (int i = 0; i < m; i++)
            bmGs[i] = m;

        // case2：模式中没有最长好后缀的子串，则在好后缀中找到
        // pattern[m-1-s…m-1]=pattern[0…s] 尽量长并匹配的子串
        for (int i = m - 1; i >= 0; i--)
            // 满足头部匹配条件
            if (suffix[i] == i + 1)
                for (int j = 0; j < m - 1 - i; j++)
                    if (bmGs[j] == m)
                        bmGs[j] = m - 1 - i;

        // case1：模式中有子串和最长好后缀完全匹配
        for (int i = 0; i <= m - 2; i++)
            bmGs[m - 1 - suffix[i]] = m - 1 - i;
    }

    private int max(int a, int b){
        return (a > b) ? a : b;
    }

    private int bm(String pattern, String text){
        /* Pre-processing */
        preBmBc(pattern);
        preBmGs(pattern);

        /* Searching */
        int m = pattern.length();
        int n = text.length();

        int j = 0;
        int i = m -1;
        
        while (j <= n - m && i >= 0) {
            if (pattern.charAt(i) == text.charAt(i + j)) {
                i--;
            } else {
                j += max(bmGs[i], bmBc[text.charAt(i + j)] - m + 1 + i);
                // 这里直接恢复为模式的最右边，可能存在重复计算问题
                // 如果模式从右向左已经匹配了 x 位，这 x 位会重复和文本作比较
                i = m - 1;
            }
        }

        if (i < 0) return j;
        return n;
    }
}

参考：algs4: bm 。从算法实现也可以看出，BM 算法和从右向左的暴力算法相比，增加预处理阶段，并且文本大范围向后移动，其他思路基本一致。BM 算法主要是改进了暴力匹配算法中，文本移动的位置；而模式中已经匹配成功的，并没有特别处理，也就是可能出现冗余的匹配计算。

时间复杂度

BM 算法在最坏情况下，和暴力匹配算法一致，时间复杂度为 O(MN)；但实际中通常情况下时间复杂度仅需 O(N/M) 。

参考文档

0%