算法 - 优先队列 - 斐波那契堆

斐波那契堆是优先队列的一种实现。

概念

斐波那契堆 Fibonacci Heap ：是一系列具有最小堆序 min-heap ordered 的有根树的集合。也就是说，每棵树都遵循最小堆性质 min-heap property：每个节点的关键字大于或等于它的父节点的关键字。（树是无序的，所以并不需要关心树是怎么排序的）

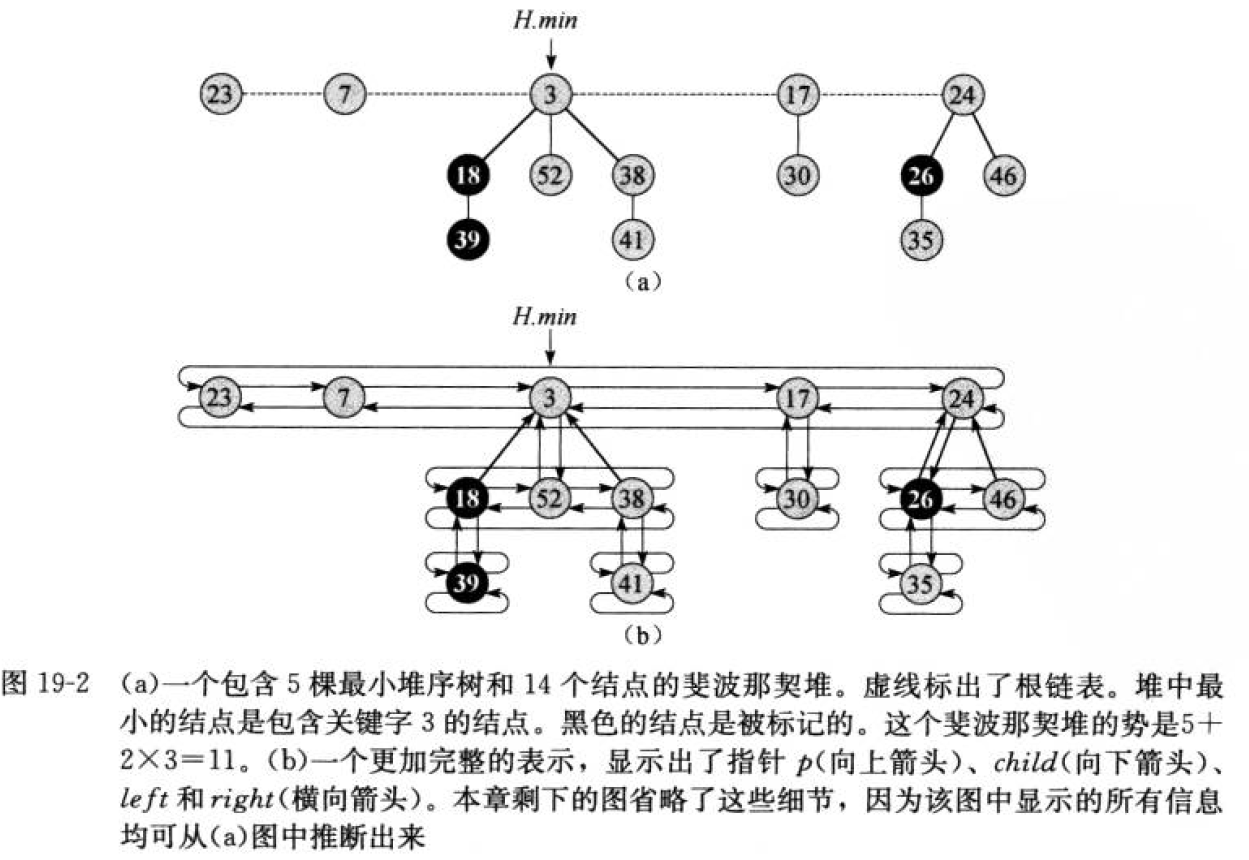
从图中可以看出，节点的所有孩子节点都被链接成一个环形的双向链表。环形双向链表在斐波那契堆中有两个优点：

可以在 O(1) 时间内从一个环形双向链表的任意位置插入一个节点和删除节点
给定两个这种链表，可以在 O(1) 时间内将他们链接成一个环形双向链表

通常使用最小关键字节点作为整个堆的入口，通过该入口可以遍历所有的堆元素。

可合并堆

可合并堆 mergeable heap 是支持以下 5 种操作的数据结构，其中每个元素都有一个关键字：

MAKE-HEAP()：创建和返回一个新的不含任何元素的堆
INSERT(H, x)：将一个已填入关键字的元素 x 插入堆 H 中
MINIMUM(H)：返回一个指向堆 H 中具有最小关键字元素的指针
EXTRACT-MIN(H)：从堆 H 中删除最小关键字的元素，并返回指向该元素的指针
UNION(H1，H2)：创建并返回一个包含堆 H1 和堆 H2 中所有元素的新堆。堆 H1 和 H2 被销毁

除了以上可合并堆的操作外，斐波那契堆还支持以下两种操作：

DECREASE-KEY(H, x, k)：将堆 H 中元素 x 的关键字赋予新值 k。假定新值 k 不大于当前的关键字
DELETE(H, x)：从堆 H 中删除元素 x

二项堆和斐波那契堆比较

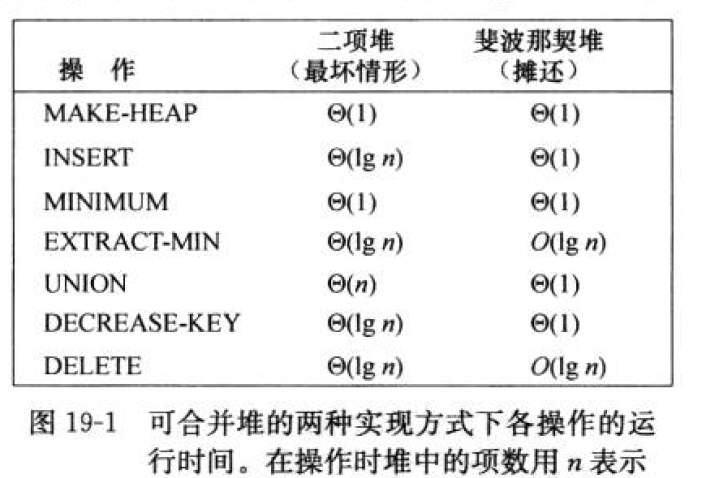
如果没有 UNION 操作，普通的二项堆操作性能已经相当好。所以斐波那契堆的优势在于合并两个堆，并且支持 DECREASE-KEY 和 DELETE 操作。
但是对于大多数应用，斐波那契堆的常数因子和编程复杂性使得它比起普通二项（或 k 项）堆并不那么适用。因此，对斐波那契堆的研究主要出于理论兴趣。如果能开发出一个简单得多的数据结构，而且它的摊还时间界与斐波那契堆相同，那么它将非常实用。

可合并堆操作

插入节点

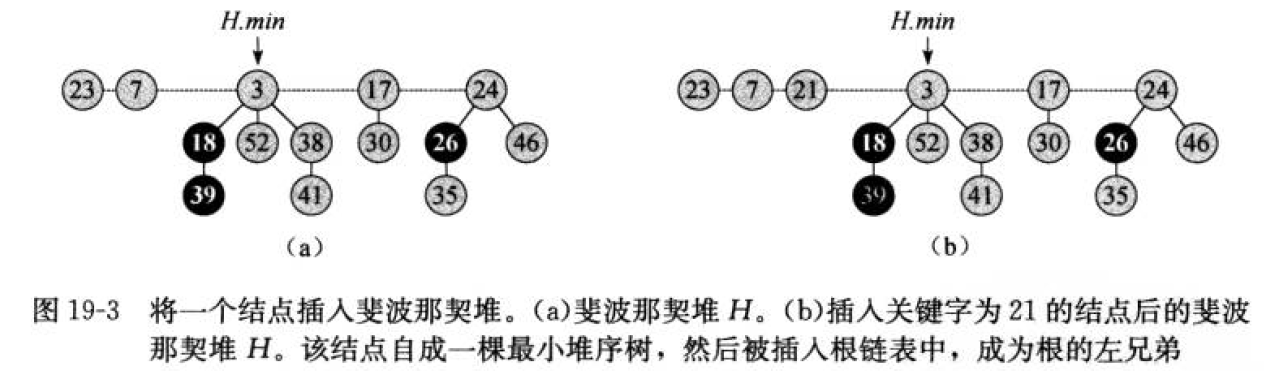
插入操作不会改变斐波那契堆的结构，直接生成新的根节点，时间复杂度为 O(1) 。

public void insert(Key key) {
    Node x = new Node();
    x.key = key;
    size++;
    head = insert(x, head);
    if (min == null) min = head;
    else              min = (greater(min.key, key)) ? head : min;
}

private Node insert(Node x, Node head) {
    if (head == null) {
        x.prev = x;
        x.next = x;
    } else {
        head.prev.next = x;
        x.next = head;
        x.prev = head.prev;
        head.prev = x;
    }
    return x;
}

本文中的算法，都是参考《算法：第四版》的实现代码。

合并

合并操作非常简单，将两个根节点链接并重新确定最小值，摊还时间为 O(1) 。

public FibonacciMinPQ<Key> union(FibonacciMinPQ<Key> that) {
    this.head = meld(head, that.head);
    this.min = (greater(this.min.key, that.min.key)) ? that.min : this.min;
    this.size = this.size+that.size;
    return this;
}

//Merges two root lists together
private Node meld(Node x, Node y) {
    if (x == null) return y;
    if (y == null) return x;
    x.prev.next = y.next;
    y.next.prev = x.prev;
    x.prev = y;
    y.next = x;
    return x;
}

取出最小值

优先队列的核心功能，就是能快速取出最小值或最大值。斐波那契堆在取出最小值后，会将堆中所有节点进行合并及调整堆的结构，并重新确定最小值。具体实现思路为：

首先将最小节点的孩子节点变为根节点，并从根链表中删掉最小节点。然后通过把具有相同度数的根节点合并的方法来链接成根链表，直到每个度数至多只有一个根在根链表中。

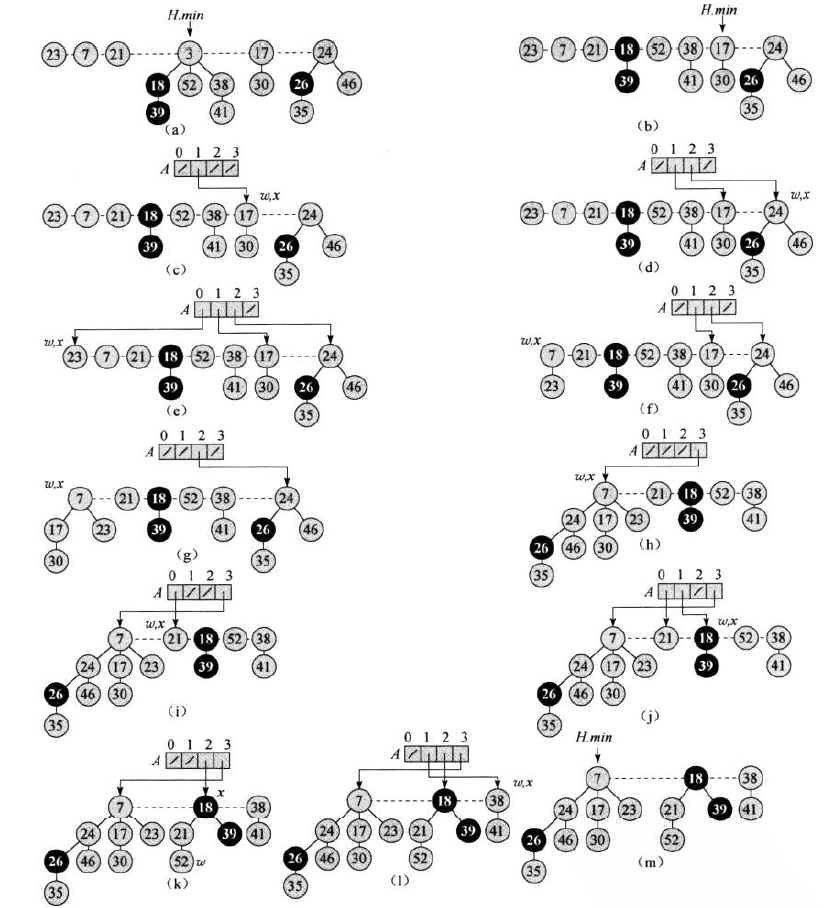
(a) 斐波那契堆 H
(b) 从根链表中移除最小值节点，并把它的孩子节点加入根链表中
(c)-(m) 过程是合并根链表，来减少斐波那契堆中树的数目，直到根链表中每一个根都有不同的度数

取出最小值操作的摊还时间为 O(logn) 。

// Deletes the minimum key
// Worst case is O(log(n)) (amortized)
public Key delMin() {
    if (isEmpty()) throw 
        new NoSuchElementException("Priority queue is empty");
    head = cut(min, head);
    Node x = min.child;
    Key key = min.key;
    min.key = null;
    if (x != null) {
        head = meld(head, x);
        min.child = null;
    }
    size--;
    if (!isEmpty()) consolidate();
    else             min = null;
    return key;
}

//Removes a tree from the list defined by the head pointer
private Node cut(Node x, Node head) {
    if (x.next == x) {
        x.next = null;
        x.prev = null;
        return null;
    } else {
        x.next.prev = x.prev;
        x.prev.next = x.next;
        Node res = x.next;
        x.next = null;
        x.prev = null;
        if (head == x)  return res;
        else             return head;
    }
}

//Coalesce the roots, thus reshapes the tree
private void consolidate() {
    table.clear();
    Node x = head;
    int maxOrder = 0;
    min = head;
    Node y = null; Node z = null;
    do {
        y = x;
        x = x.next;
        z = table.get(y.order);
        while (z != null) {
            table.remove(y.order);
            if (greater(y.key, z.key)) {
                link(y, z);
                y = z;
            } else {
                link(z, y);
            }
            z = table.get(y.order);
        }
        table.put(y.order, y);
        if (y.order > maxOrder) maxOrder = y.order;
    } while (x != head);
    head = null;
    for (Node n : table.values()) {
        if (n != null) {
            min = greater(min.key, n.key) ? n : min;
            head = insert(n, head);
        }
    }
}

//Assuming root1 holds a greater key than root2, 
//root2 becomes the new root
private void link(Node root1, Node root2) {
    root2.child = insert(root1, root2.child);
    root2.order++;
}

降键值和删除

降键值 `DECREASE-KEY`

斐波那契堆中降键值涉及到几个关键点：

被降键值的节点，会被执行切断 cuting 操作，切断该节点和其父节点的链接，使它成为根节点
如果节点的一个孩子节点被切断，它将会被标记；如果失去两个孩子节点，它将被切断。也就是该节点会成为根节点
如果被标记的节点，其父节点也被标记了，当该节点被切断时，父节点将也会被切断，这个过程为级联切断 cascading-cut

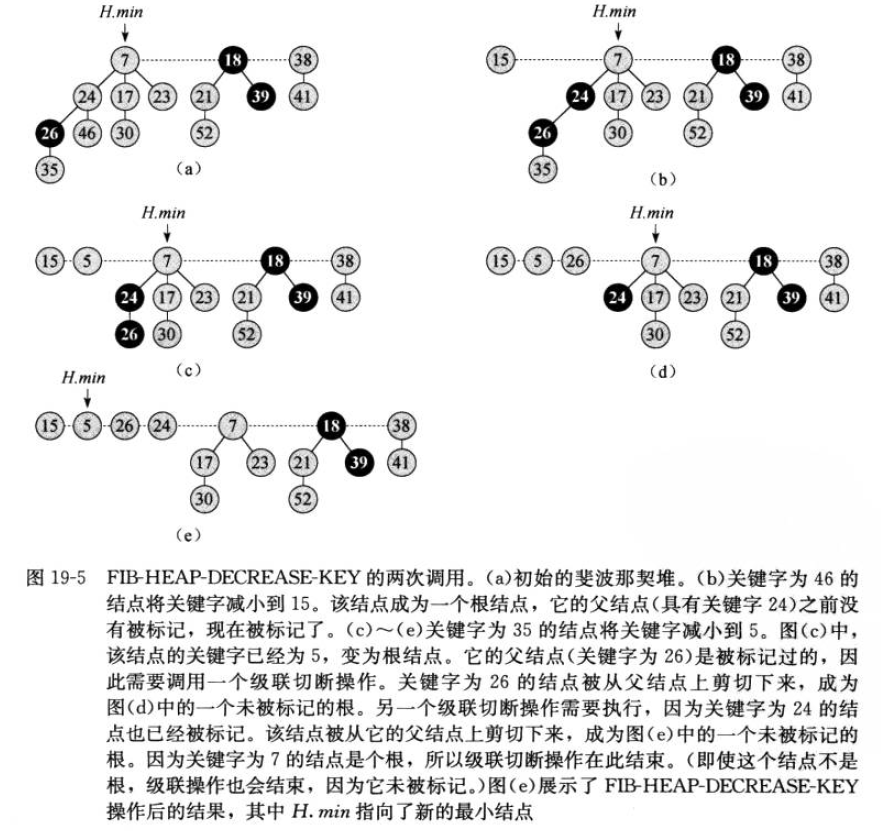
也就是被降键值的节点，一定会成为根节点。如果最小值变更，只需要从新在根节点链表中找到最小值就行。

《算法：第四版》中使用的是索引斐波那契堆来实现降键值，因为和斐波那契堆是两个数据结构，暂时不参考该代码实现。

删除

删除的思路是：

将该节点降键值到负无穷
删除该最小键值

动画演示

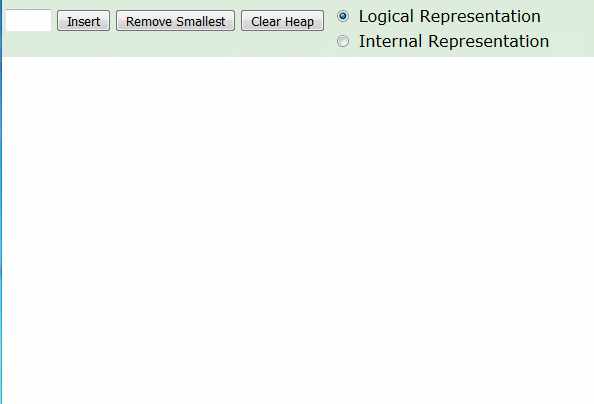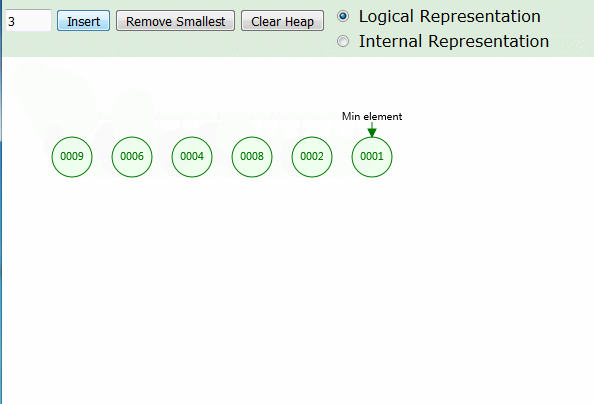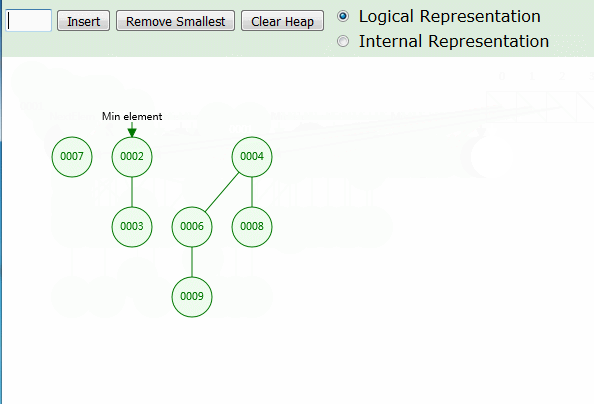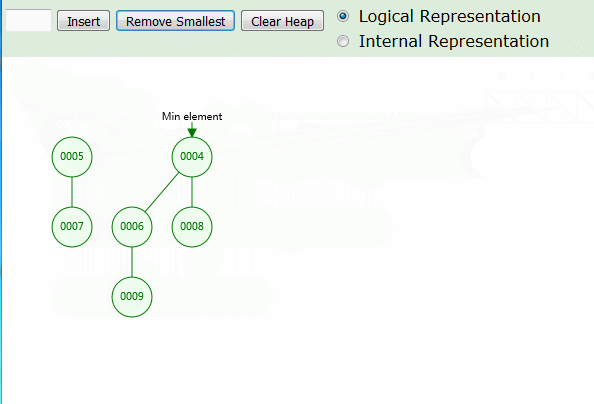
动画中可以看出，为了性能平衡，插入时仅需 O(1) ，直接插入最小值左边，并作为根节点存在。删除最小值时，才会将堆合并。

小结

斐波那契堆的降键值功能，可以在一些问题上得到应用：单源最短路径、加权二分图匹配，最小生成树等问题。不过根据我们前面对图相关问题的分析，可以使用索引优先队列二项堆，或者优先队列删除再插入来替代降键值功能。

概念