介绍机器学习,深度学习,神经网络基础。
基础
概念
AI: Artificial Intelligence 人工智能,它是研究、开发用于模拟、延伸和扩展人的智能的理论、方法、技术及应用系统的一门新的技术科学。ML: Machine Learning 机器学习,它是人工智能的子集;机器学习从有限的观测数据中学习或猜测出具有一般性的规律,并将这些规律应用到未观测样本上的方法。DL: Deep Learning 深度学习,它是机器学习的子集;深度学习通过建立具有阶层结构的人工神经网络 ANNs:Artifitial Neural Networks ,在计算系统中实现人工智能。
监督学习/无监督学习
- 监督学习
supervised learning
每个输入数据都有对应标签Label,则为监督学习。监督学习中经典算法为分类、回归、统计,常见的为KNN, SVN等。常见应用场景有:垃圾邮件识别、图像识别、房价预测等等。 - 无监督学习
unsupervised learning
只有输入数据,没有任何标签,则为无监督学习。无监督学习有聚类Clustering,主成分分析PCA等。常见应用场景有:新闻聚合、内容挖掘等。 - 半监督学习
semi-supervised learning
对于半监督学习,其训练数据的一部分是有标签的,另一部分没有标签,而没标签数据的数量常常极大于有标签数据数量(这也是符合现实情况的)。常见应用场景:医疗影像、金融风控。 - 强化学习
reinforcement learning
强化学习是指没有任何的标签,但有一系列的奖励和惩罚规则,计算机通过不断尝试,从错误中学习,最后找到规律。常见应用场景有:AlphaGo,在线广告系统,工业机器人等。
分类和回归
分类和回归的本质是一样的,都是对输入做出预测,其区别在于输出的类型:
- 分类问题
输出是离散型变量,如+1、-1,是一种定性输出。例如预测明天天气是阴、晴还是雨。 - 回归问题
输出是连续型变量,是一种定量输出。例如预测明天的温度是多少度。
神经网络
人工神经网络 ANNs:Artificial Neural Networks 简称为神经网络 NN ,是神经科学家模仿人脑神经系统设计的数学模型;在机器学习领域,神经网络由很多人工神经元构成的网络结构模型,这些神经元之间的连接是可学习的参数。
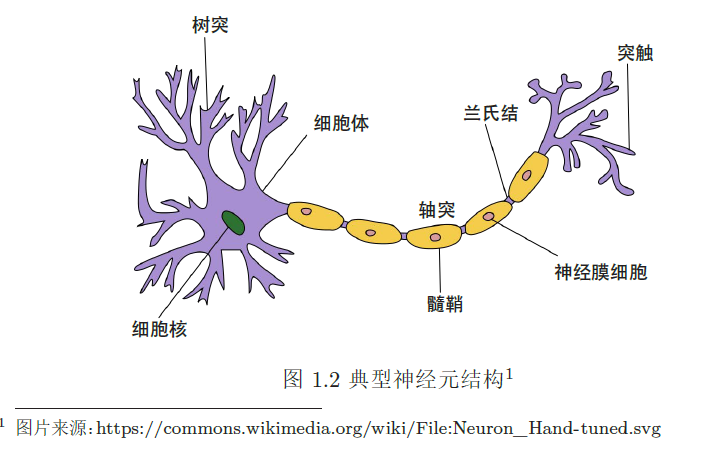
一个典型的神经元数学结构示例:
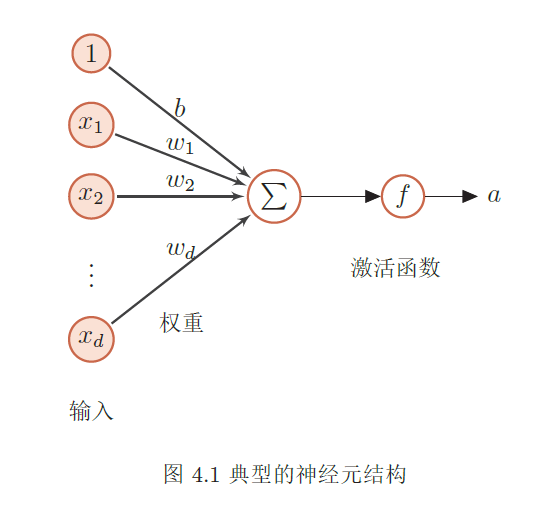
其中:输入为 x1, x2, ... ,权重为 w1, w2, ... ,偏置为 b ,激活函数为 f 。
前馈神经网络
前馈神经网络 Feedforward Neural Network 简称前馈网络,是人工神经网络的一种。在此种神经网络中,各神经元从输入层开始,接收前一级输入,并输出到下一级,直至输出层。整个网络中无反馈,可用一个有向无环图表示。
前馈神经网络采用一种单向多层结构。其中每一层包含若干个神经元,同一层的神经元之间没有互相连接,层间信息的传送只沿一个方向进行。其中第一层称为输入层。最后一层为输出层.中间为隐含层,简称隐层。隐层可以是一层,也可以是多层。
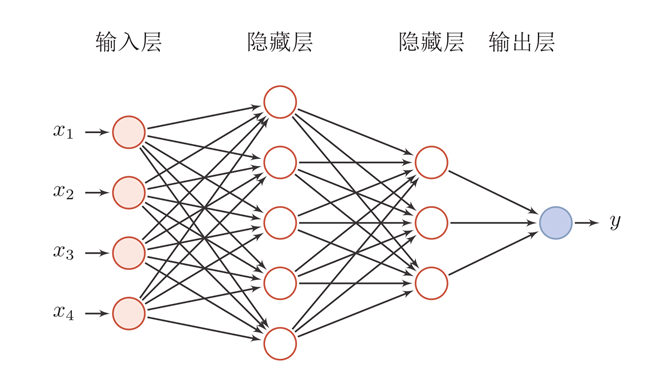
神经网络的层数:一般不计入输入层,层数为 n 个隐藏层加上 1 个输出层。前馈神经网络使用数学表达式来表示为:

根据通用近似定理 Universal Approximation Theorem ,对于具有线性输出层和至少一个使用“挤压”性质的激活函数的隐藏层组成的前馈神经网络,只要其隐藏层神经元的数量足够,它可以以任意的精度来近似任何从一个定义在实数空间 Rd 中的有界闭集函数。也就是说,神经网络在某种程度上可以作为一个“万能”函数来使用,可以用来进行复杂的特征转换,或逼近一个复杂的条件分布。
常见激活函数
激活函数 Activation Function 在神经元模型中非常重要,增强了网络的表示能力和学习能力,激活函数具备的几点性质:
- 连续并可导(允许少数点上不可导)的非线性函数。可导的激活函数可以直接利用数值优化的方法来学习网络参数
- 激活函数及其导函数要尽可能的简单,有利于提高网络计算效率
- 激活函数的导函数的值域要在一个合适的区间内,不能太大也不能太小,否则会影响训练的效率和稳定性
常见激活函数有: sigmoid, tanh, relu 等等。
Sigmoid函数Sigmoid型函数是指一类S型曲线函数,为两端饱和函数。常用的Sigmoid型函数有Logistic函数和Tanh函数;通常在实际使用中,Sigmoid会特指为Logistic函数。
对于函数f(x):若x → −∞时,其导数f′(x) → 0,则称其为左饱和;若x → +∞时,其导数f′(x) → 0,则称其为右饱和。当同时满足左、右饱和时,就称为两端饱和。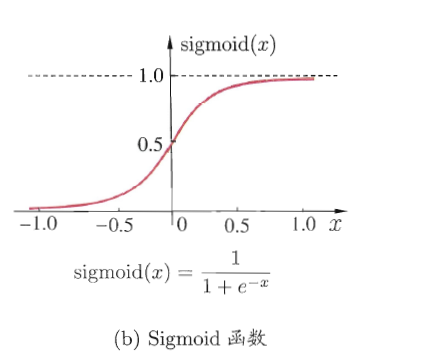
Tanh函数Tanh函数也是Sigmoid型的一种,其曲线和数学表达式如下: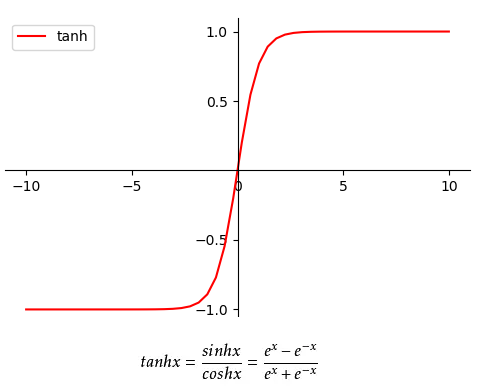
ReLU函数ReLU: Rectified Linear Unit修正线性单元,是目前深层神经网络中最常用的激活函数。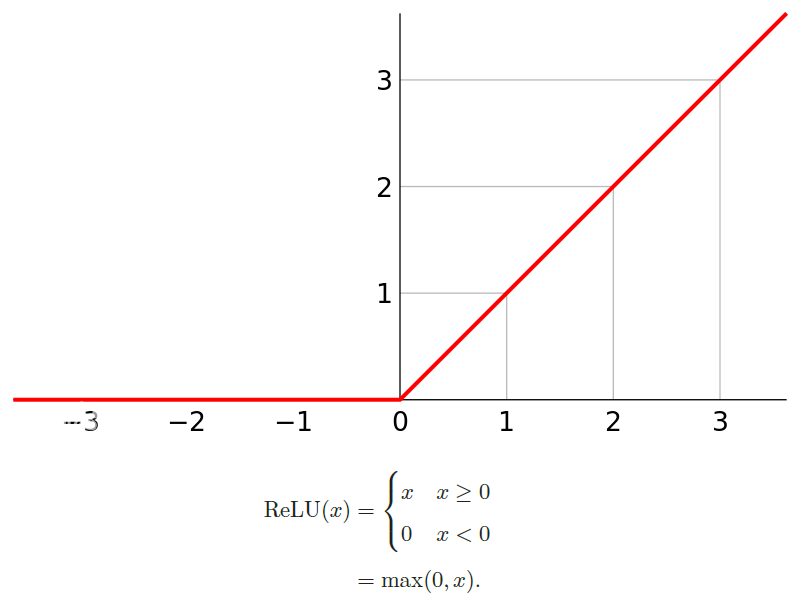
ReLU 激活函数的优缺点:
- 优点
ReLU的神经元只需要进行加、乘和比较的操作,计算上更加高效。Sigmoid型激活函数会导致一个非稀疏的神经网络,而ReLU却具有很好的稀疏性,大约 50% 的神经元会处于激活状态。在优化方面,相比于Sigmoid型函数的两端饱和,ReLU函数为左饱和函数,且在x>0时导数为 1 ,在一定程度上缓解了神经网络的梯度消失问题,加速梯度下降的收敛速度。 - 缺点
ReLU函数的输出是非零中心化的,给后一层的神经网络引入偏置偏移,会影响梯度下降的效率。此外在训练时,当输入小于 0 时,输出全部为 0 ,使得梯度为 0 ,这种现象称为死亡ReLU问题Dying ReLU Problem。
反向传播
反向传播 BP: BackPropagation 算法在 1970 年代提出,大概 1986 年由 Hinton 等人在神经网络上发扬光大。
给定一个样本 (x, y) ,通过神经网络模型后得到的输出为 ˆy ,假设损失函数为 L(y, ˆy) ,计算损失函数关于每个参数的导数。
对第 l 层中的参数 W(l) 和 b(l) 计算偏导数, ∂L(y,ˆy)/∂W(l) 的计算涉及到矩阵的微分十分繁琐,因为满足 z(l) = W(l)a(l−1) + b(l) ,根据导数的链式法则:

计算出每一层的误差项之后,我们就可以得到每一层参数的梯度;因此反向传播算法训练过程为:
- 前馈计算每一层的净输入
z(l)和激活值a(l),直到最后一层 - 反向传播计算每一层的误差项
δ(l) - 计算每一层参数的偏导数,并更新参数
使结果误差反向传播从而得出权重 w 调整的梯度。通过不断迭代,对参数矩阵进行不断调整后,使得输出结果的误差值更小,使输出结果与事实更加接近。
常见损失函数
损失函数 loss function ,有时也称为残差函数 error function 或者代价函数 cost function ,就是用来表现预测与实际数据的差距。反向传播算法的目标是将损失函数降到最低。
损失函数的计算有很多方法,常见的有:均方误差 MSE ,平均绝对误差 MAE ,交叉熵 CE 等等。
- 均方误差
MSE: Mean Square Error
也称为L2损失函数,计算方法:目标值和预测值之差的平方再求平均: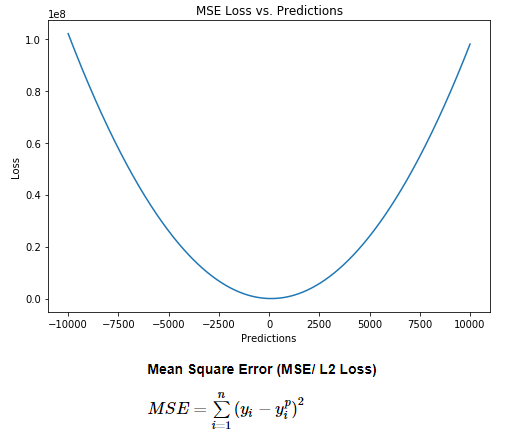
- 平均绝对误差
MAE: Mean Absolute Error
也称为L1损失函数,计算方法:目标值与预测值之差绝对值的和,表示了预测值的平均误差幅度,而不需要考虑误差的方向: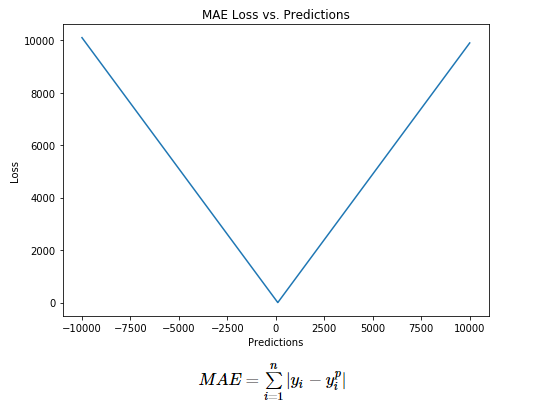
- 交叉熵
CE: Cross Entropy
交叉熵损失函数是一个平滑函数,用于度量两个概率分布间的差异性信息,交叉熵越低,策略越好。
如下图所示中:C是类别数(比如猫、狗、其他动物等),n是总样本,yc,i是第i个样本真实类别c,pc,i是第i个样本预测为类别c的概率。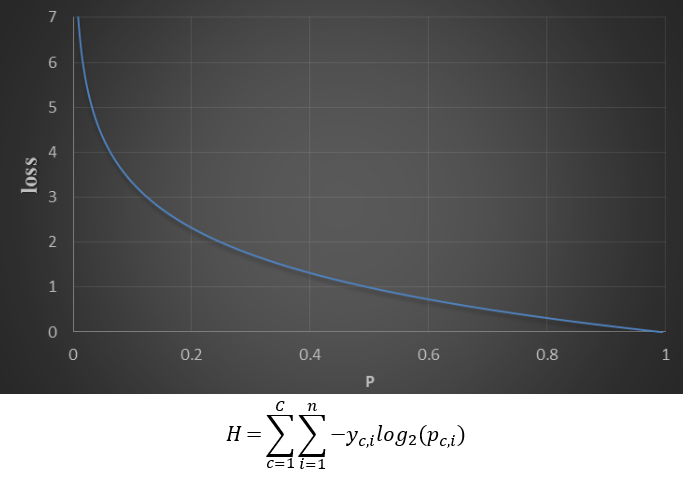
在分类应用中:交叉熵损失函数通常和 Softmax 多分类器或者 Sigmoid 二分类器一起使用。
梯度消失/爆炸
在深度神经网络中的梯度是不稳定的,在靠近输入层的隐藏层中可能会出现梯度消失 Vanishing Gradient Problem 或梯度爆炸 Exploding Gradient Problem。梯度不稳定的原因是,在反向传播过程中,前面层上的梯度是来自后面层上梯度的乘积。当神经网络层数越多时,梯度就会越不稳定。
- 梯度消失
前面的网络层比后面的网络层梯度变化更小,故权值变化缓慢,从而引起了梯度消失问题,也称为梯度弥散。 - 梯度爆炸
前面的网络层比后面的网络层梯度变化更快,引起了梯度爆炸的问题。
根据导数链式法则,梯度的变化由激活函数决定, Sigmoid 激活函数很容易出现梯度消失现象,所以通常使用 ReLU 激活函数。
优化器
反向传播中,优化器提供了计算损失函数梯度更新的方法,常见优化器有:梯度下降 gradient descent , momentum 优化器, adam 优化器,等等,参考论文:
下图是常见优化器的比较:
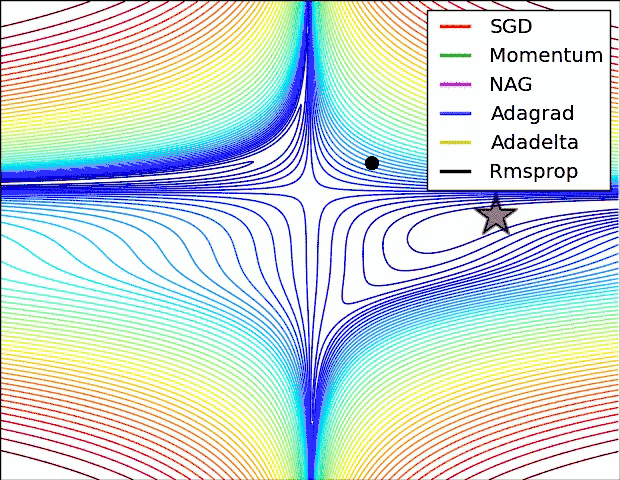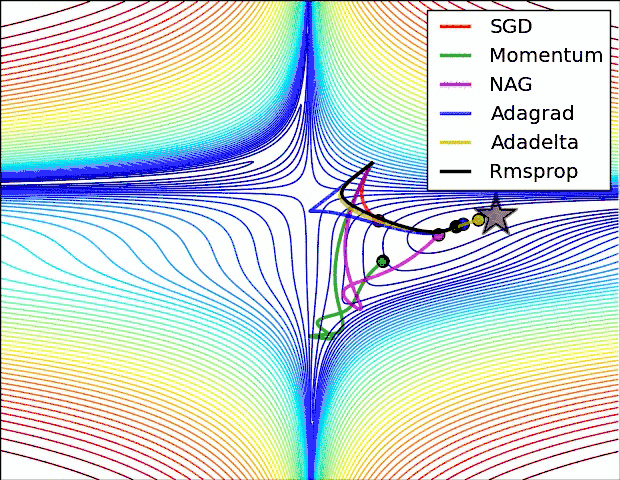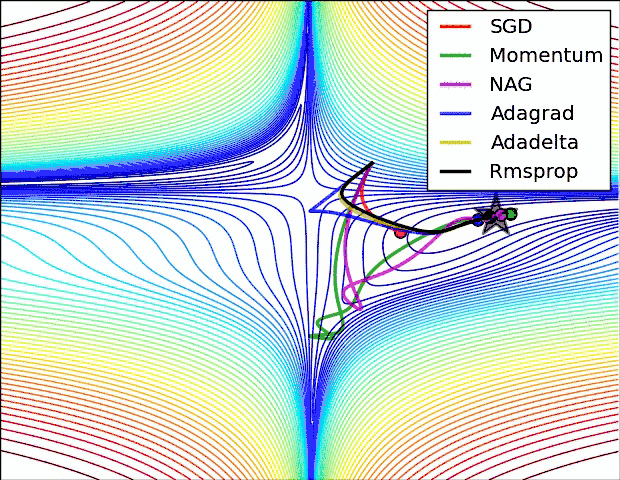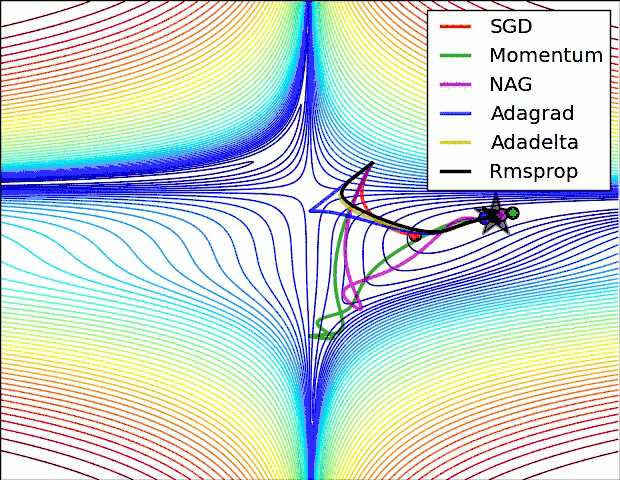
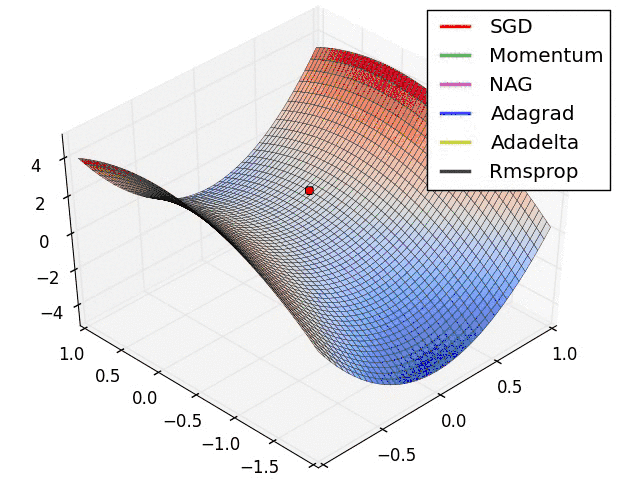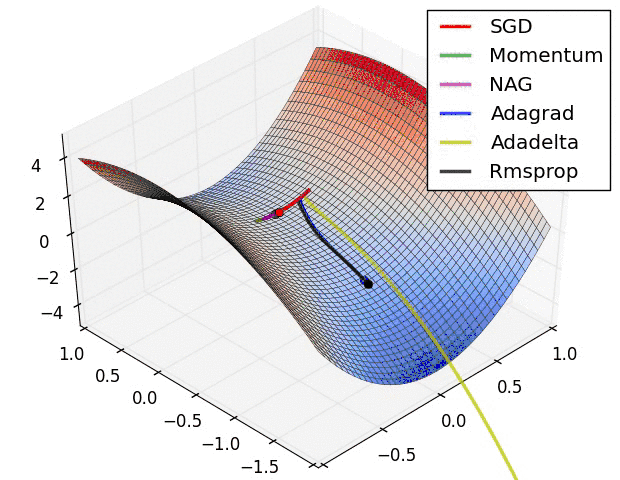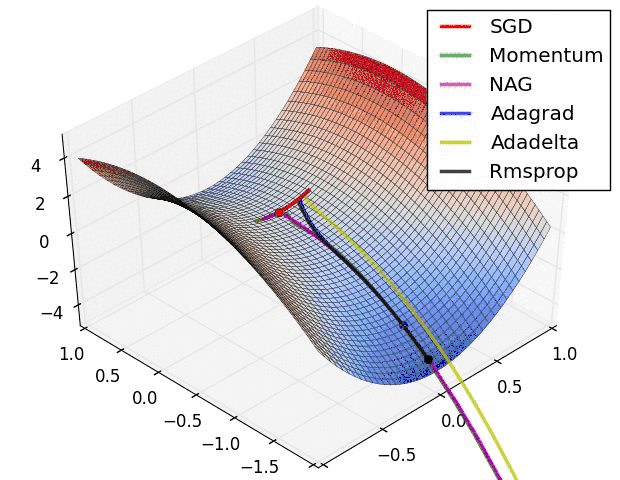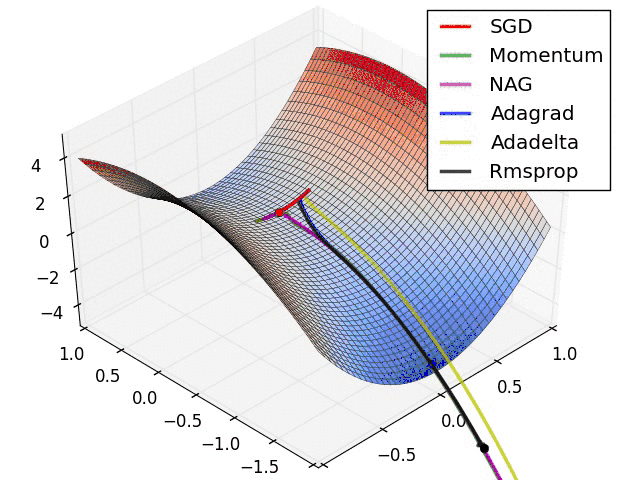
神经网络优化
过拟合
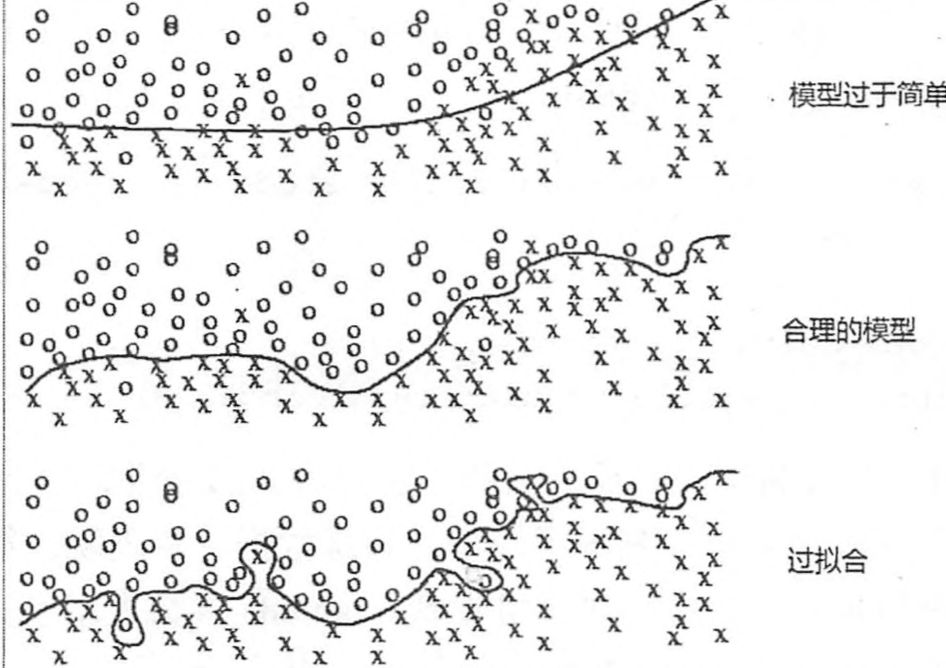
过拟合 overfit :神经网络模型在训练数据集上的准确率较高,但在新的数据进行预测或分类时准确率较低,说明模型的泛华能力差。
正则化
正则化 Regularization :用于增加训练误差为代价来减少测试集上的误差的策略或技术;常见的技术有:
- 数据集增强
Data Agumentation - 提前终止
Early Stopping - 参数范数惩罚
Parameter Norm Penalties Dropout
参数范数惩罚:在损失函数中添加一个惩罚项,约束模型的学习能力;即给每个参数权重 w 进行惩罚,引入模型复杂度指标,从而抑制模型噪声,减小过拟合。常见的有 L1, L2 正则化,其中 L1 正则化惩罚的是权重 w 的绝对值,在损失函数求导数时,意味着如果 w 为正数时, w 减小趋于 0 ;如果 w 为负数时, w 增加趋于 0 ; L1 的思路就是把权重往 0 靠,从而降低网络复杂度。通常在需要压缩模型时使用 L1 ,其他情况使用 L2 。其中 λ 是正则化超参数,通常设为 0.001 。
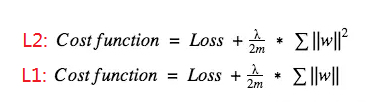
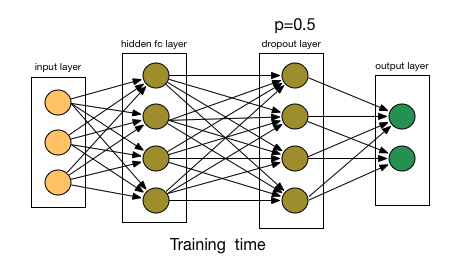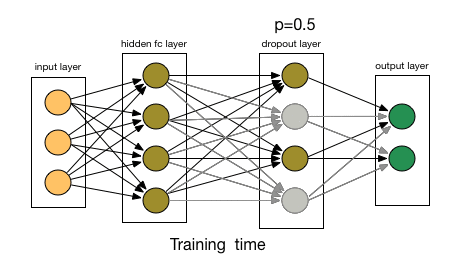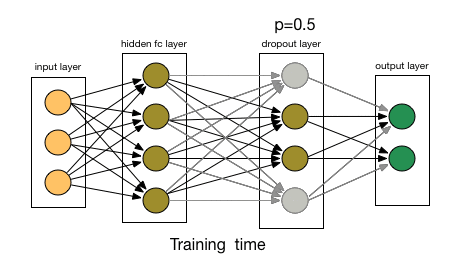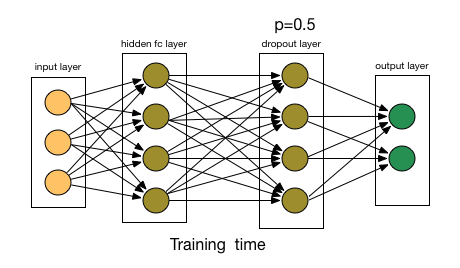
Dropout 通过改变神经网络的结构来增强网络的泛化能力。在用前向传播算法和反向传播算法训练模型时,随机的从全连接 DNN 网络中去掉一部分隐含层的神经元; Dropout 可以看作是模型组合,每次生成的网络结构都不一样,通过组合多个模型来减少过拟合。
学习率
学习率 Learning rate :是一个超参数。在训练过程中,参数的更新向着损失函数梯度下降的方向,学习率决定了参数每次更新的幅度。当学习率选择过大时会出现震荡不收敛;选择过小时会出现收敛速度慢的情况。
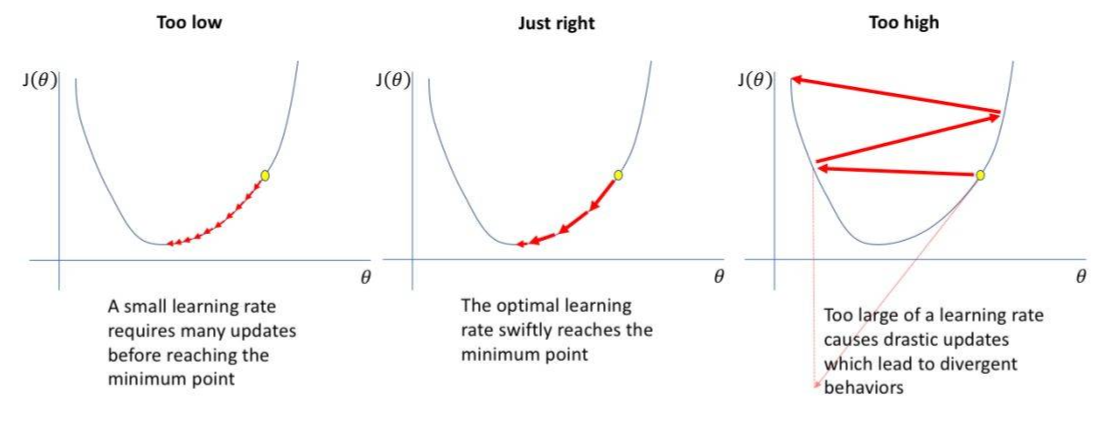
因此选择一个合适的学习率非常重要,但是实际训练中往往并不清楚该超参数设置成什么值,通常动态来设置学习率,即学习率退火 learning rate annealing :先从比较高的学习率开始,然后在训练中慢慢降低学习率。常有两种实现方法:
- 线性衰减
每经过n轮训练后,将学习率减少一半。 - 指数衰减
每经过n轮训练后,学习率指数改变。这里有一个tensorflow中提供的计算公式:decayed_learning_rate = learning_rate*decay_rate^(global_step/decay_steps),其中learning_rate, decay_rate是两个超参数,分别表示初始学习率和底数;global_step表示当前训练的轮数,decay_steps表示多少轮更新一次学习率。
初始学习率和底数通常设置为learning_rate=0.001, decay_rate=0.99。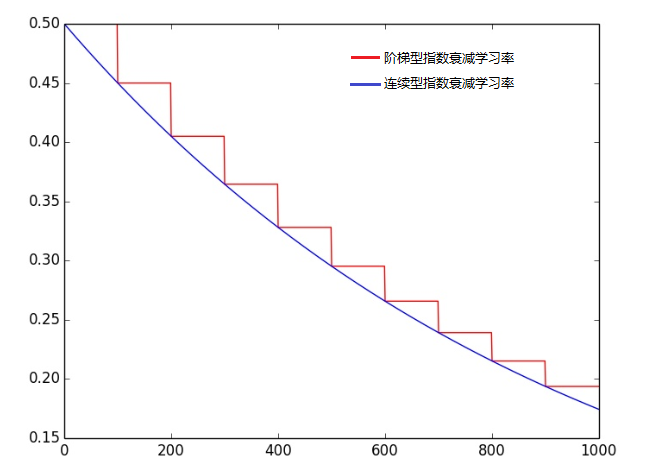
滑动平均
滑动平均 ema:exponential moving average 或者叫做指数加权平均 exponentially weighted moving average ,可以用来估计变量的局部均值,使得变量的更新与一段时间内的历史取值有关。滑动平均记录了一段时间内模型中所有参数 w 和 b 各自的平均值,利用滑动平均值可以增强模型的泛化能力。
滑动平均对每一个变量会维护一个影子变量 shadow variable ,这个影子变量的初始值就是相应变量的初始值,而每次运行变量更新时,影子变量的值会被更新;滑动平均影子计算公式:shadow_variable = decay * shadow_variable + (1 - decay) * variable ,其中 decay 是超参数,表示衰减率,决定了影子变量的更新速度; decay 越大影子变量越趋于稳定。在实际运用中,decay 一般会设成非常接近 1 的数,比如 0.99 , 0.999 等等。
在 tensorflow 中为了使得影子变量在训练前期可以更新更快,滑动平均还提供了 num_updates 参数动态设置 decay 的大小。衰减率计算公式:decay=min(decay, (1 + num_updates) / (10 + num_updates)) , num_updates 表示多少轮更新一次。
偏差和方差
偏差 Bias :度量了学习算法的期望预测与真实结果的偏离程度,即刻画了学习算法本身的拟合能力。
方差 Variance :度量了同样大小的训练集的变动所导致的学习性能的变化,即刻画了数据扰动所造成的影响。
欠拟合 underfit :模型不能适配训练样本,有一个很大的偏差。
过拟合 overfit :模型很好适配训练样本,但在测试集上表现很糟,有一个很大的方差。
下图很好的说明的偏差和方差和模型选择的关系:
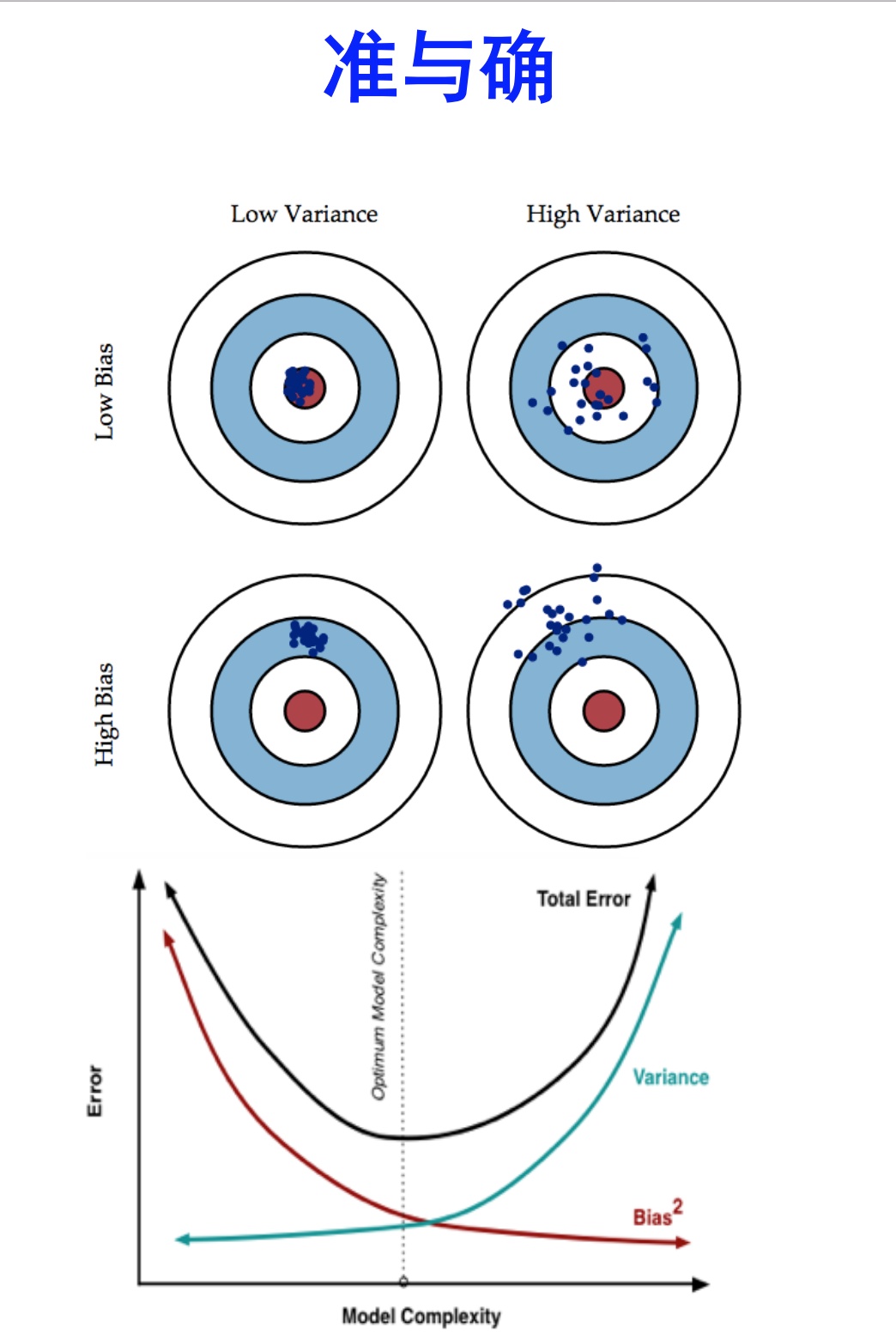
模型越复杂,拥有更好的数据拟合能力,获得更低的偏差,但是会导致过拟合而出现方差过大。
在模型评估中,根据偏差和方差结果绘制出的图形可以看出,针对偏差和方差过大解决方法如下:
- 偏差过大,即欠拟合
- 寻找更好的特征(具有代表性)
- 用更多的特征(增大输入向量的维度,增加模型复杂度)
- 方差过大,即过拟合
- 增大数据集合,使用更多的数据,噪声点比减少(减少数据扰动所造成的影响)
- 减少数据特征,减少数据维度,高维空间密度小(减少模型复杂度)
- 正则化方法
- 交叉验证法
偏差和方差用来描述模型的好坏,以及模型需要优化的方向。