算法 - 数据结构和算法

发表于 | 分类于 | 阅读次数

介绍算法基础知识，算法书籍推荐等；常见算法分析方法：贪心、分治、动态规划以及摊还分析等；常见数据结构基础介绍。

算法介绍

书籍推荐

  • 算法
    通常说的橙书，指的就是《算法-第四版》，由普林斯顿大学教授 Robert Sedgewick 和 Kevin Wayne 共同编写，使用 Java 实现了教材中的所有算法。
    官网信息：官网 ，网页包含一部分章节的电子书，以及一些代码链接；算法测试数据集 。
    代码地址：官网 github 。
    习题答案：官网课后习题答案 ，知乎关于课后习题答案 。
    公开课：公开课-1 ，公开课-2 。

  • 算法导论
    《算法导论》由 Thomas H.Cormen、Charles E.Leiserson、Ronald L.Rivest、Clifford Stein 四人合作编著，通常简称为 CLRs 。所有算法都用伪代码描述，包含大量严格的数学证明。学习资料：网易公开课 ，coursera公开课 。

  • 数据结构与算法分析
    《数据结构与算法分析：C 语言描述》 由佛罗里达国际大学计算机学院教授 Mark Allen Weiss 编写，C 语言实现的算法。目录结构和国内教材非常类似，适合入门。

  • 学习路线
    《算法导论》包含了大量数学相关知识，《算法》写的更通俗易懂，推荐先从《算法》开始学习。但是《算法导论》中的算法似乎更通用，《算法》中的算法实现加入了很多作者的优化和想法。知乎高票答案：如何学习数据结构 ，《算法导论》 还是先看完 《算法 第四版》 ，算法的作用。

算法可视化

算法通过动画来演示效果，能非常直观的体现算法过程。有两个非常有用的可视化网站：

算法博客推荐

其他可能有用的信息

算法刷题网站

数据结构和算法

我们关注的大多数算法都需要适当地组织数据，而为了组织数据就产生了数据结构，数据结构也是计算机科学研究的核心对象，它和算法的关系非常密切。数据结构是算法的副产品或是结果，因此要理解算法必须学习数据结构。简单的算法也会产生复杂的数据结构，相应地复杂的算法也许只需要简单的数据结构。

算法分析方法

贪心

贪心算法 greedy algorithms ：在对问题求解时，总是做出在当前看来是最好的选择。也就是说，不从整体最优上加以考虑，他所做出的是在某种意义上的局部最优解。贪心算法终止时，希望局部最优就是全局最优解；否则算法只能得到次最优解。
贪心选择是指所求问题的整体最优解可以通过一系列局部最优的选择，即贪心选择来达到。这是贪心算法可行的第一个基本要素，也是贪心算法与动态规划算法的主要区别。贪心选择是采用从顶向下、以迭代的方法做出相继选择，每做一次贪心选择就将所求问题简化为一个规模更小的子问题。对于一个具体问题，要确定它是否具有贪心选择的性质，我们必须证明每一步所作的贪心选择最终能得到问题的最优解。通常可以首先证明问题的一个整体最优解，是从贪心选择开始的，而且作了贪心选择后，原问题简化为一个规模更小的类似子问题。然后，用数学归纳法证明，通过每一步贪心选择，最终可得到问题的一个整体最优解。

  • 最优子结构
    当一个问题的最优解包含其子问题的最优解时，称此问题具有最优子结构性质。运用贪心策略在每一次转化时都取得了最优解。问题的最优子结构性质是该问题可用贪心算法或动态规划算法求解的关键特征。贪心算法的每一次操作都对结果产生直接影响，而动态规划则不是。贪心算法对每个子问题的解决方案都做出选择，不能回退；动态规划则会根据以前的选择结果对当前进行选择，有回退功能。动态规划主要运用于二维或三维问题，而贪心一般是一维问题。
  • 示例
    贪心最通用的示例为：找零钱。通常我们都会优先使用大额钞票 50，再其次 20，依次到最小的 1 角；虽然找零钱有各种方式，但是贪心策略能最快得到解。其他常见贪心算法应用：最短路径树 Dijkstra 算法、最小生成树 Prim 算法、最小生成树 Kruskal 算法等。

分治

分治 divide and conquer 算法，由两部分组成：

  • 分 divide ：递归解决较小的问题（基本情况除外）
  • 治 conquer ：从子问题的解构建原问题的解

分治算法的基本思想是将一个规模为 N 的问题分解为 K 个规模较小的子问题，这些子问题相互独立且与原问题性质相同。求出子问题的解，就可得到原问题的解。即一种分目标完成程序算法，简单问题可用二分法完成。

分治算法基本上都是递归实现（算法中至少出现两个递归调用才算分治），但是有些递归调用（算法中只有一次递归调用）并不算是分治算法，而只是化简到一个更简单的情况。

  • 分治递归
    常见的有：二分搜索、树的遍历（左子树、右子树），归并排序，快速排序等。 

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    // 归并排序示例
    private static void sort(Comparable[] a, Comparable[] aux, 
        int lo, int hi) {
        if (hi <= lo) return;
        int mid = lo + (hi - lo) / 2;
        // 至少有两个递归
        sort(a, aux, lo, mid);
        sort(a, aux, mid + 1, hi);
        merge(a, aux, lo, mid, hi);
    }

  • 简单递归
    常见的有：二叉查找树查找算法，并查集查找，图的深度搜索等等，这些算法不是分治算法，只是进行了一次递归调用。 

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    // 图的深度搜索
    private void dfs(Graph G, int v) {
        count++;
        marked[v] = true;
        for (int w : G.adj(v)) {
            if (!marked[w]) {
                parent[w] = v;
                // 仅仅进行一次递归调用
                dfs(G, w);
            }
        }
    }

分治算法对应的时间复杂度通常为 O(NlogN) 。

动态规划

动态规划 DP: Dynamic Programming 是运筹学的一个分支，是求解决策过程最优化的数学方法。动态规划算法通常用于求解具有某种最优性质的问题。在这类问题中，可能会有许多可行解。每一个解都对应于一个值，我们希望找到具有最优值的解。动态规划算法与分治法类似，其基本思想也是将待求解问题分解成若干个子问题，先求解子问题，然后从这些子问题的解得到原问题的解。与分治法不同的是，适合于用动态规划求解的问题，经分解得到子问题往往不是互相独立的。若用分治法来解这类问题，则分解得到的子问题数目太多，有些子问题被重复计算了很多次。如果我们能够保存已解决的子问题的答案，而在需要时再找出已求得的答案，这样就可以避免大量的重复计算，节省时间。我们可以用一个表来记录所有已解的子问题的答案。不管该子问题以后是否被用到，只要它被计算过，就将其结果填入表中。
动态规划算法与分治算法最大的差别是：适合于用动态规划法求解的问题，经分解后得到的子问题往往不是互相独立的（即下一个子阶段的求解是建立在上一个子阶段的解的基础上，进行进一步的求解）。另外，分治法中使用的递归效率较低，通常会利用动态规划思想将算法写成非递归的方式，并把子问题的答案系统的记录在表中。

摊还分析

摊还分析 amortized analysis ：我们求数据结构的一个操作序列中所执行的所有操作的平均时间，来评价操作的代价。即使序列中某个单一操作的代价很高，但是一个操作的平均代价是很低的。摊还分析并不同于平均情况，不涉及概率，可以保证最坏情况下每个操作的平均性能。
摊还分析中最常用的三种技术：

  • 聚合分析 aggregate analysis
    该方法用来确定一个 n 个操作的序列的总代价的上界 T(n)，因此每个操作的平均代价为 T(n)/n 。我们将平均代价作为每个操作的摊还代价，因此所有操作具有相同的摊还代价。
  • 核算法 accounting method
    用来分析每个操作的摊还代价，当存在不止一种操作时，每种操作的摊还代价可能是不同的。核算法将序列中某些较早的操作的“余额”作为“预付信用”存储起来，与数据结构中的特定对象相关联。在操作序列中随后的部分，存储的信用即可用来为那些缴费少于实际代价的操作支付差额。
  • 势能法 potential method
    与核算法类似，势能法也是分析每个操作的摊还代价，而且也是通过较早操作的余额来补偿稍后操作的差额。势能法将信用作为数据结构的“势能”存储起来，与核算法不同，它将势能作为一个整体存储，而不是将信用与数据结构中单个对象关联分开储存。

基础数据结构

表

我们将处理一般的形如 A1, A2, A3, ... , An 的表 list，我们称这个表的大小为 N 。大小为 0 的表为空表 empty list 。对于除空表外的任何表，说 Ai+1 后继 Ai，并称 Ai-1 前驱 Ai 。
表支持查找、插入、删除等基本操作。表可以通过简单数组或链表的形式实现。

数组和链表

  • 数组
    在内存中数组是一块连续的区域，使用前需要预留空间，即使没有利用也会占用内存。不利用扩展，扩容时需要重新申请大数组，并拷贝整个原数组。插入和删除效率低，但是随机访问速度快（下标直接访问）。
  • 链表
    不要求内存是连续的，每个数据都保存了下一个数据的地址。不用指定大小，方便扩展。插入和删除效率高，但是随机访问效率低，需要逐个数据遍历一遍。

数组和链表是最基本的数据结构，单独或者组合使用，是所有复杂数据结构的数据存储器。

队列和栈

  • 栈
    特点：LIFO: Last In First Out，后进先出。也就是插入和删除只能在栈顶操作，分别为进栈 Push 和出栈 Pop 。
  • 队列
    特点：FIFO: First In First Out，先进先出。队列固定在一端进入另一端出去，分别为入队 Enqueue/Offer 和出队 Dequeue/Poll 。

栈和队列都是表，所以都可以通过数组或链表来实现。栈通常用于保存方法调用顺序，逆波兰表达式等等；队列适合任何需要排队实现的应用场景。

树

树的基本概念

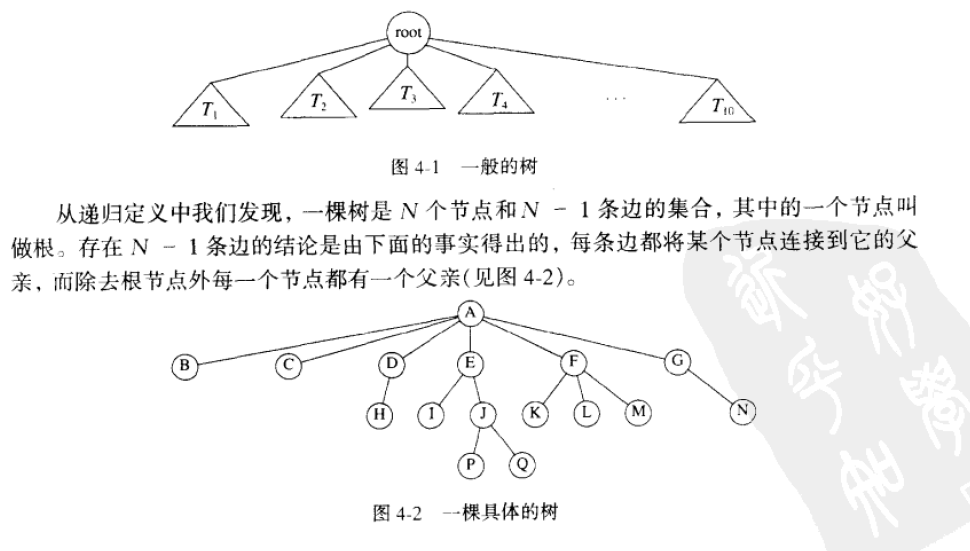
树 Tree ：定义树的一种自然的方式是递归方法，一棵树是一些节点的集合。这个集合可以是空集；若非空，则一棵树由根 root 节点 r 以及 0 个或多个非空子树 T1, T2...Tk 组成，这些子树中每一颗的根都被根 r 的边 edge 连接。

  • 子父节点：每颗子树的根叫做根 r 的儿子 child 或者子节点；而根 r 是每颗子树根的父亲 parent 或者父节点
  • 树叶：每个节点可以有任意多个子节点，也可能是 0 个子节点；没有儿子的节点称为树叶 leaf
  • 兄弟：具有相同父亲的节点称为兄弟 sibling
  • 深度：任意节点的深度 depth 是从根到该节点边的条数。根的深度为 0
  • 高度：树的高度 height 是从根到树叶的最长路径

0088-tree.png

二叉树

二叉树 binary tree 是一棵树，其中每个节点都不能有多于两个的儿子。

二叉查找树

二叉查找树 Binary Search Tree，又称二叉排序树 BST: Binary Sort Tree 、二叉搜索树；详解参考：算法 - 二叉查找树 。
二叉查找树：是一颗二叉树，其中每个节点都含有一个 Comparable 的键（以及相关联的值），其中每个节点的键都大于左子树中的任意节点的键，并且小于右子树中的任意节点的键。

红黑树

红黑树首先是一颗二叉查找树，详解参考：算法 - 红黑树 ；红黑树同时满足 5 条性质：

  • 每个节点要么是红色要么就是黑色
  • 根节点必须是黑色
  • 每个空（NIL）节点必须是黑色
  • 如果节点是红色，它的两个子节点必须是黑色
  • 树是完美黑色平衡的：即任意空 NIL 节点到根节点路径上包含相同数量的黑色节点

其他常见查找树

  • B 树
    B 树：B-tree, Balanced tree, 也就是平衡树，也称为 B-, B_ 树，它是一种平衡的多叉树。2-3 树是最简单的 B 树。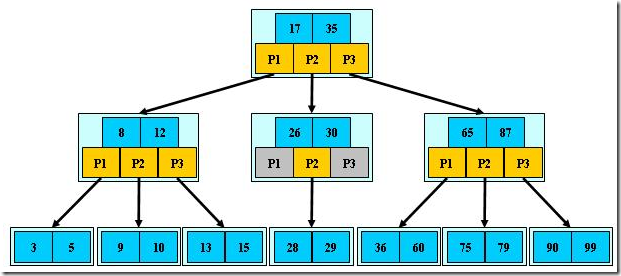
    0084-data-structure-tree-b-tree.png
  • B+ 树
    B+ 树是 B- 树的变体，也是一种多路搜索树。为叶子结点增加链表指针，所有关键字都在叶子结点中出现，非叶子结点作为叶子结点的索引。B+ 树总是到叶子结点才命中，适合文件索引系统。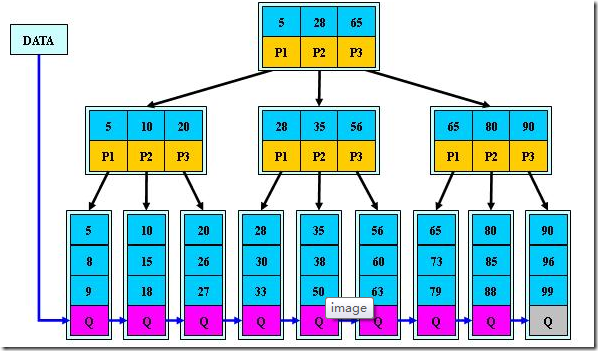
    0084-data-structure-tree-b-plus-tree.png
  • B* 树
    B* 树是 B+ 树的变体，为非叶子结点也增加链表指针，提高节点利用率。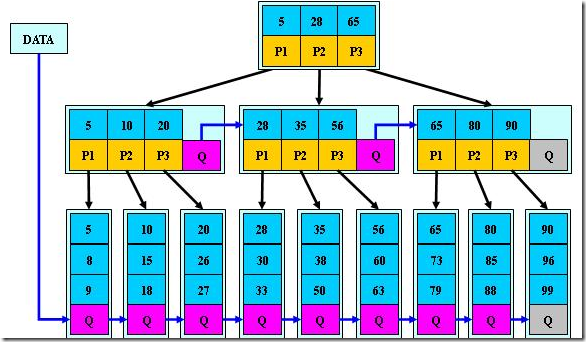
    0084-data-structure-tree-b-star-tree.png

图

图是一组顶点和一组能够将两个顶点相连的边组成的，详情参考：算法 - 图的基础概念 。四种重要的图模型：

  • 无向图
    简单连接。无向图是由一组顶点和一组能够将两个顶点相连的边组成的。
  • 有向图
    连接有方向性。有向图由一组顶点和一组有方向的边组成，每条有方向的边都连接着有序的一对顶点。
  • 加权图无向图
    无向图的每条边，连接带有权值。
  • 加权有向图
    有向图的每条边，连接既有方向性又带有权值。

常见数据结构

散列表

也称为哈希表，通过把关键码值映射到表中一个位置来访问记录，以加快查找的速度。这个映射函数叫做散列函数，存放记录的数组叫做散列表。详情参考：Java HashMap 简介

  • 散列函数
    散列函数能使对一个数据序列的访问过程更加迅速有效，通过散列函数，数据元素将被更快地定位。
  • 处理冲突
    散列表解决冲突的两种方式：拉链法和线性探测法。线性探测法的提前条件就是：大小为 M 的数组保存 N 个键值对，其中 M > N，也就是数组要足够大。

优先队列

优先队列 Priority queue ：是这样一种数据结构，支持删除优先级最高元素和插入元素。通常有两种实现方式：

  • 最大优先队列
    支持删除最大元素，也称为大根堆。
  • 最小优先队列
    支持删除最小元素，也称为小根堆。

优先队列有多种实现方式，常见的有：算法 - 优先队列 - 二叉堆 ，算法 - 优先队列 - 斐波那契堆 。

并查集

并查集 Union-Find ，也称为不相交集。一个不相交集合数据结构 disjoint-set data structure 维护了一个不相交动态集的集合 S={S1, S2, S3, ..., Sk}。我们用一个代表 representative 来标识这个集合，它是这个集合的某个成员。详情参考：算法 - 并查集 ；这个数据结构支持下面三个操作：

  • MAKE-SET(x) ：集
  • UNION(x, y) ：并
  • FIND-SET(x) ：查

数据结构设计思路

  • 理清需要解决什么问题
  • 设计对应的 API 接口
  • 使用 API 设计测试程序
  • 设计合适的数据结构
  • 使用匹配的算法实现

API 接口设计作用是将使用和实现分离，以实现模块化编程。先定义 API 有两个目标：一是希望测试用例的代码清晰且正确（测试驱动）；二是希望这些操作确实是可以实现的。

参考文档

  • 《算法：第四版》
  • 《算法导论：第 3 版》
  • 《数据结构与算法分析：C 语言描述》
0%