算法 - 二叉查找树

发表于 | 分类于 | 阅读次数

算法：二叉查找树。

二叉查找树

定义

二叉查找树 Binary Search Tree，又称二叉排序树 BST: Binary Sort Tree 、二叉搜索树。
二叉查找树：是一颗二叉树，其中每个节点都含有一个 Comparable 的键（以及相关联的值），其中每个节点的键都大于左子树中的任意节点的键，并且小于右子树中的任意节点的键。

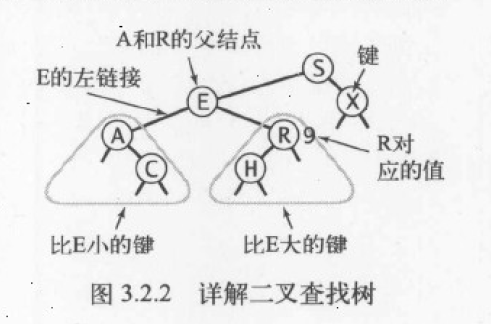
0088-binary-search-tree.png

数据表示

一颗二叉查找树代表了一组键值的集合，而同一个集合可以有多颗不同的二叉查找树表示。但这些二叉查找树在垂直方向上的投影：都是固定顺序的，由小到大的排序顺序。

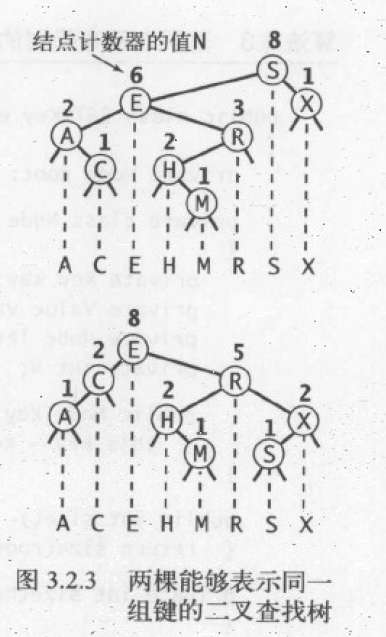
0085-binary-search-tree-same-order.png

数据结构解析

节点

1
2
3
4
5
6
7
8
9
10
11
12
private class Node {
    private Key key;           // sorted by key
    private Value val;         // associated data
    private Node left, right;  // left and right subtrees
    private int size;          // number of nodes in subtree

    public Node(Key key, Value val, int size) {
        this.key = key;
        this.val = val;
        this.size = size;
    }
}

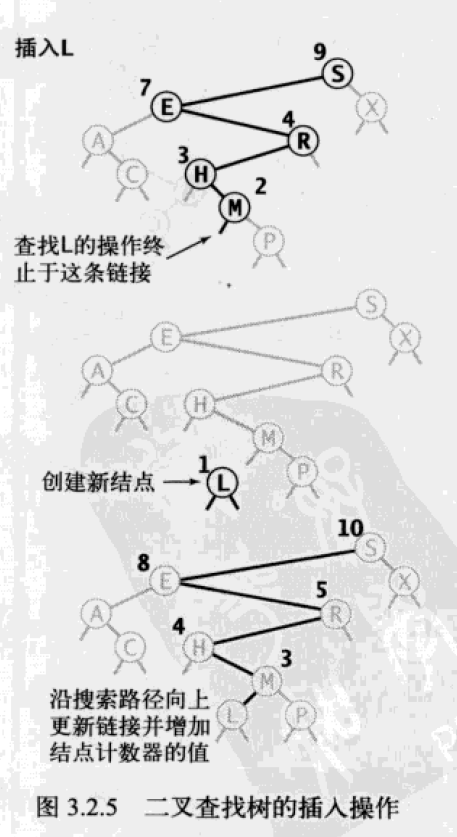
插入 insert

插入操作用来构造一颗二叉查找树。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public void insert(Key key, Value val){
    if(key == null || val == null) return;
    root = insert(root, key, val);
}

// 递归算法
private Node insert(Node x, Key key, Value val) {
    // 如果没有查找到 key，则新建节点
    if (x == null) return new Node(key, val, 1);
    
    // key 和当前节点比较：小则插入左子树，大则插入右子树
    // 相等则更新 key 对应的 value
    int cmp = key.compareTo(x.key);
    if      (cmp < 0) x.left  = insert(x.left,  key, val);
    else if (cmp > 0) x.right = insert(x.right, key, val);
    else              x.val   = val;
    
    // 更新子树节点数量
    x.size = 1 + size(x.left) + size(x.right);
    return x;
}

插入示意图：

0088-bst-insert-show.png

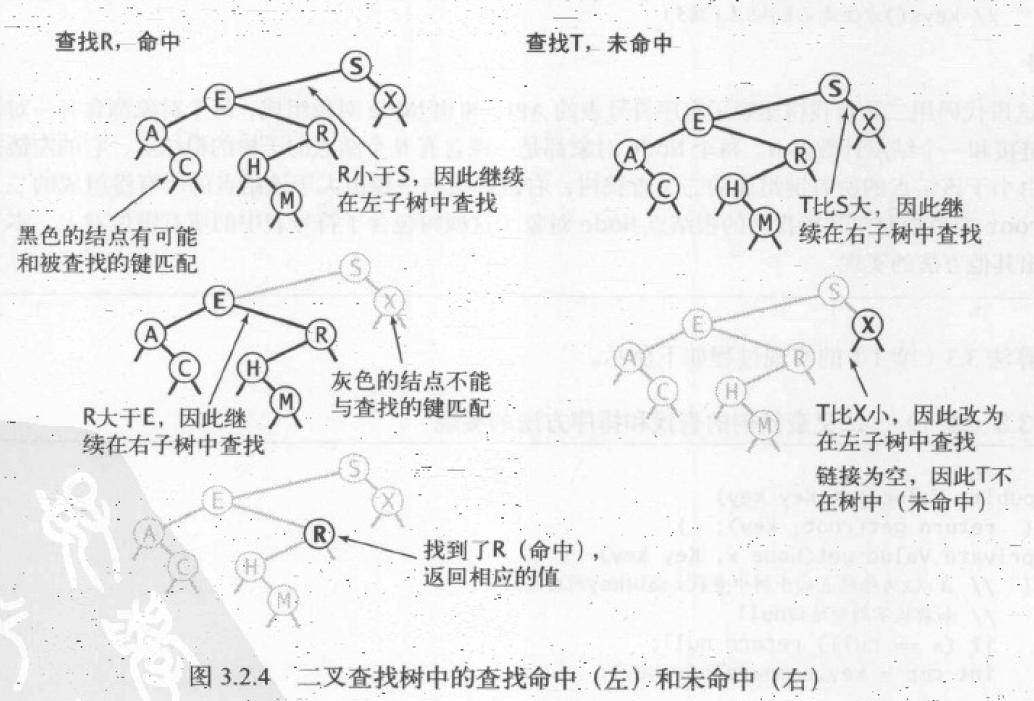
查找 find

在二叉查找树中，查找指定的关键字。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public Value find(Key key){
    return find(root, key);
}

// 递归算法
private Value find(Node x, Key key) {
    if (key == null || x == null) return null;
    
    // key 和当前节点比较：小则查找左子树，大则查找右子树
    // 相等表示查找到 key 对应的 value
    int cmp = key.compareTo(x.key);
    if      (cmp < 0) return find(x.left, key);
    else if (cmp > 0) return find(x.right, key);
    else              return x.val;
}

查找示意图：

0088-bst-search-result.png

性能分析

二叉查找树的算法性能取决于二叉树的形状，而二叉查找树的形状取决于键被插入的先后顺序。最好情况下是完全平衡的二叉树，N 个节点查找的时间复杂度为 logN；最坏情况下时间复杂度会达到 N 。

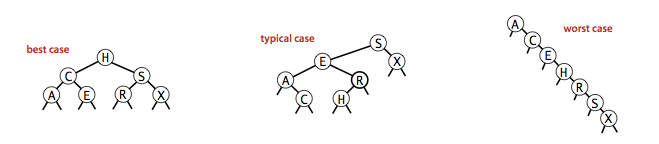
0088-bst-best-typical-worst-case.png

有序性

二叉查找树得到广泛应用的一个重要原因是：始终能保持键的有序性，不管是插入、删除等操作，二叉查找树始终是一个排好序的数据结构。

最大值和最小值

  • 最大值始终在右子树
  • 最小值始终在左子树 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
// 最小值  
public Key min() {
    if (isEmpty()) throw new NoSuchElementException("empty symbol table");
    return min(root).key;
} 

private Node min(Node x) { 
    if (x.left == null) return x; 
    else                return min(x.left); 
}

// 最大值  
public Key max() {
    if (isEmpty()) throw new NoSuchElementException("empty symbol table");
    return max(root).key;
} 

private Node max(Node x) {
    if (x.right == null) return x; 
    else                 return max(x.right); 
}

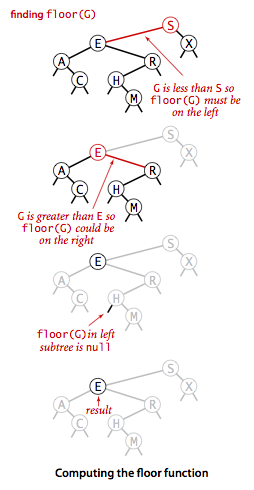
向上取整和向下取整

  • 向上取整：找到大于等于指定 key 的最小 key
  • 向下取整：找到小于等于指定 key 的最大 key 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
// 向上取整
public Key ceiling(Key key) {
    if (key == null) throw new IllegalArgumentException("argument is null");
    if (isEmpty()) throw new NoSuchElementException("empty symbol table");
    
    Node x = ceiling(root, key);
    if (x == null) return null;
    else return x.key;
}

private Node ceiling(Node x, Key key) {
    if (x == null) return null;
    
    int cmp = key.compareTo(x.key);
    if (cmp == 0) return x;
    if (cmp < 0) { 
        Node t = ceiling(x.left, key); 
        if (t != null) return t;
        else return x; 
    } 
    return ceiling(x.right, key); 
}

// 向下取整
public Key floor2(Key key) {
    return floor2(root, key, null);
}

private Key floor2(Node x, Key key, Key best) {
    if (x == null) return best;
    int cmp = key.compareTo(x.key);
    if      (cmp  < 0) return floor2(x.left, key, best);
    else if (cmp  > 0) return floor2(x.right, key, x.key);
    else               return x.key;
}

向下取整搜索示意图：

0088-bst-floor.png

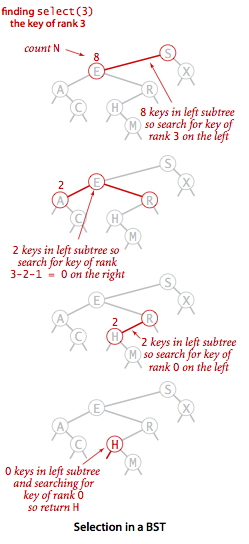
选择和排名

  • 选择：找出第 k 个排序位置的键值
  • 排名：给定键值 key 的排序位置

二叉查找树的节点中 size 保存了以该节点为根的子树，一共包含多少子节点（包含自己），计算方式为：size(r) = size(r.left) + size(r.right) + 1;。不管是选择还是排名，都和位置有关系，也就是和节点数有关。所以计算位置时，直接以节点数来判断。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
// 选择  
public Key select(int k) {
    if (k < 0 || k >= size()) {
        throw new IllegalArgumentException("argument  is invalid: " + k);
    }
    
    Node x = select(root, k);
    return x.key;
}

// Return key of rank k. 
private Node select(Node x, int k) {
    if (x == null) return null; 
    
    int t = size(x.left); 
    if      (t > k) return select(x.left,  k); 
    // 选择右子树时，需要扣除左子树中的节点总数
    else if (t < k) return select(x.right, k-t-1); 
    else            return x; 
}

// 排名  
public int rank(Key key) {
    if (key == null) throw new IllegalArgumentException("argument is null");
    return rank(key, root);
} 

// Number of keys in the subtree less than key.
private int rank(Key key, Node x) {
    if (x == null) return 0; 
    
    int cmp = key.compareTo(x.key); 
    if      (cmp < 0) return rank(key, x.left); 
    // 排名右子树时，需要加上左子树的节点总数
    else if (cmp > 0) return 1 + size(x.left) + rank(key, x.right); 
    else              return size(x.left); 
}

选择示意图：

0088-bst-select.png

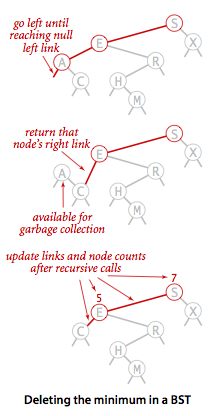
删除最大键和最小键

  • 删除最小键
    最小键的左子树一定为空，右子树可以为空或者非空；删除时将右子树赋给父节点左子树。
  • 删除最大键
    最大键的右子树一定为空，左子树可以为空或者非空；删除时将左子树赋给父节点右子树。
  • 更新节点数
    删除键值时，需要注意更新所在子树中每个节点的 size 值。 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
// 删除最小值
public void deleteMin() {
    if (isEmpty()) throw new NoSuchElementException("Symbol table null");
    root = deleteMin(root);
}

private Node deleteMin(Node x) {
    // 如果左子树为空，x 即为最小值，返回其右子树
    if (x.left == null) return x.right;
    // 最小值始终在左子树
    // 将找到的最小值节点的右子树赋给父节点左子树
    x.left = deleteMin(x.left);
    // 递归更新节点数
    x.size = size(x.left) + size(x.right) + 1;
    return x;
}

// 删除最大值
public void deleteMax() {
    if (isEmpty()) throw new NoSuchElementException("Symbol table null");
    root = deleteMax(root);
}

private Node deleteMax(Node x) {
    // 如果右子树为空，x 即为最大值，返回其左子树
    if (x.right == null) return x.left;
    // 最大值始终在右子树
    // 将找到的最大值节点的左子树，赋给父节点右子树
    x.right = deleteMax(x.right);
    // 递归更新节点数
    x.size = size(x.left) + size(x.right) + 1;
    return x;
}

删除最小值示意图：

0088-bst-deletemin.png

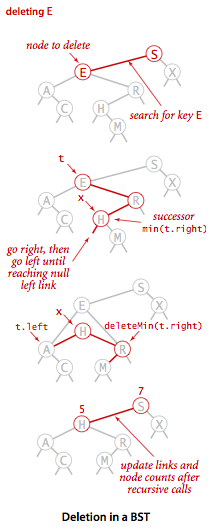
删除指定键值

删除最小值或最大值的方法，只适合删除包含一个子节点或没有子节点的节点。但如果一个节点拥有两个子节点，该如何删除？T.Hibbard 在 1962 年提出了解决方案：删除一个节点时，使用其后继节点来填补它的位置。后继节点为其右子树中的最小节点（当然也可以取左子树的最大节点），这样替换后仍能保持二叉查找树的有序性。详细步骤如下：

  • 被删除的节点 x 保存为 t
  • 将 x 赋值为后继节点，即 min(t.right)
  • x 的右子树删除最小值，并更新 x 右子树
  • x 的左子树保持不变
  • 递归更新子树所有节点数 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
public void delete(Key key) {
    if (key == null) throw new IllegalArgumentException("null key");
    root = delete(root, key);
}

private Node delete(Node x, Key key) {
    if (x == null) return null;

    int cmp = key.compareTo(x.key);
    if      (cmp < 0) x.left  = delete(x.left,  key);
    else if (cmp > 0) x.right = delete(x.right, key);
    else { 
        if (x.right == null) return x.left;
        if (x.left  == null) return x.right;
        // 被删除节点保存为 t
        Node t = x;
        // 更新值为后继节点
        x = min(t.right);
        // 右子树删除最小值并更新
        x.right = deleteMin(t.right);
        // 左子树保持不变
        x.left = t.left;
    } 
    // 递归更新节点数
    x.size = size(x.left) + size(x.right) + 1;
    return x;
}

删除指定键值示意图：

0088-bst-delete.png

范围查找

使用队列保存指定范围内查找到的键值。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
// 输出所有键值
public Iterable<Key> keys() {
    if (isEmpty()) return new Queue<Key>();
    return keys(min(), max());
}

// 输出指定范围键值
public Iterable<Key> keys(Key lo, Key hi) {
    if (lo == null || hi == null) 
        throw new IllegalArgumentException("key is null");

    Queue<Key> queue = new Queue<Key>();
    keys(root, queue, lo, hi);
    return queue;
} 

private void keys(Node x, Queue<Key> queue, Key lo, Key hi) { 
    if (x == null) return; 
    int cmplo = lo.compareTo(x.key); 
    int cmphi = hi.compareTo(x.key); 
    // 如果下界比键值小，遍历左子树
    if (cmplo < 0) keys(x.left, queue, lo, hi); 
    // 如果键值落入范围，入队
    if (cmplo <= 0 && cmphi >= 0) queue.enqueue(x.key); 
    // 如果上界比键值大，遍历右子树
    if (cmphi > 0) keys(x.right, queue, lo, hi); 
}

小结

二叉查找树的几个特点：

  • 性能和输入序列顺序高度相关
  • 插入和查找的平均时间复杂度都为 logN
  • 插入、删除等操作，始终能保持键的有序性

参考文档

0%