算法 - 最短路径树基础以及 Dijkstra 算法

介绍最短路径基础概念；以及 Dijkstra 算法 - 迪科斯彻算法：解决边权重非负的加权有向图的单点最短路径问题。

最短路径基础概念

名词

• 最短路径
  在一幅加权有向图中，从顶点 s 到顶点 v 的最短路径是所有从 s 到 v 的路径中的权重最小者。
• 最短路径树
  SPT: Shortest Path Tree，给定一幅加权有向图和顶点 s，以 s 为起点的一颗最短路径树是图的一幅子图，它包含 s 和从 s 可达的所有顶点。这颗有向树的根顶点为 s，树的每条路径都是有向图中的一条最短路径。

边的松弛

松弛 relaxation ，对于每个顶点 v 来说：

• v.d
  假设 v.d 用来记录从起点 s 到达顶点 v 的最短路径权重的上界。我们称 v.d 为 s 到 v 的最短路径估计。
• v.π
  假设 v.π 表示顶点 v 的前驱顶点。

松弛过程：将从起点 s 到顶点 u 之间的最短路径距离加上顶点 u 与 v 之间的边权重，并与当前 s 到 v 的最短路径估计进行比较，如果前者更小，则对 v.d, v.π 进行更新。

// 初始化所有顶点
// 每个顶点最短路径估计为无穷大，前驱顶点为空
INITIALIZE-SINGLE-SOURCE(G, s)
    for each vertex v ∈ G.V
        v.d = ∞
        v.π = NIL
    s.d=0

// 松弛，并更新 v 的前驱顶点为 u
// w 表示权重
RELAX(u,v,w)
    if v.d > u.d + w(u,v)
        v.d = u.d + w(u,v)
        v.π = u

松弛操作的时间复杂度为 O(1) 。

最短路径的最优性条件

最优性条件：G 是一幅加权有向图，顶点 s 是 G 的起点，distTo[] 是一个由顶点索引的数组，保存的是 G 中路径的长度。对于从 s 可达的所有顶点 v，distTo[v] 的值是从 s 到 v 的某条路径的长度，对于从 s 不可达的所有顶点 v，该值为无穷大。当且仅当对于从 v 到 w 的任意一条边 e，这些值都满足 distTo[w] <= distTo[v] + e.weight() 时（换句话说，不存在有效边时），它们是最短路径长度。

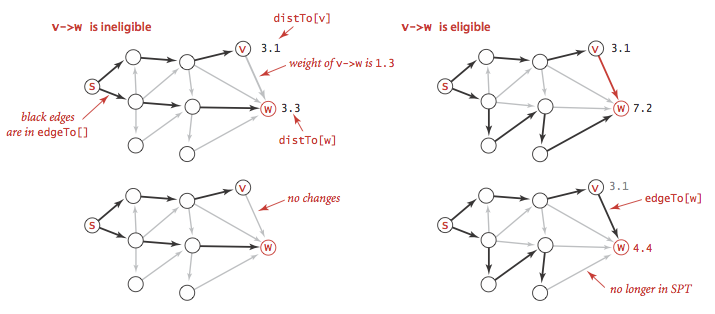
边的松弛实现：放松边 v-w 意味着检查从 s 到 w 的最短路径是否先从 s 到 v，然后再由 v 到 w。如果是，则比较 distTo[w] 和 distTo[v] + e.weight() 的大小。如果 distTo[w] 小，则 v-w 这条边失效了；否则将 distTo[w] 更新为较小值。distTo[] 记录顶点到该点的最短路径。

private void relax(DirectedEdge e){
    int v = e.from(), w = e.to();
    if(distTo[w] > distTo[v] + e.weight()){
        distTo[w] = distTo[v] + e.weight();
        edgeTo[w] = e;
    }
}

最优性条件是所有最短路径算法证明的基础，即只要满足不等式 distTo[w] <= distTo[v] + e.weight() ，则这条路径必为最短路径。

通用最短路径算法

一个定义明确且可以解决的加权有向图最短路径问题的算法：

• 对于起点不可达的顶点，最短路径为正无穷
• 对于起点可达但路径上某个顶点属于一个负权重环的顶点，最短路径为负无穷
• 对于所有其他顶点，计算最短路径及最短路径树

将 distTo[s] 初始化为 0 ，其他 distTo[] 元素初始化为无穷大，继续如下操作：放松 G 中的任意边，直到不存在有效边为止。
对于任意从 s 可达的顶点 w ，在进行这些操作之后，distTo[w] 的值即为从 s 到 w 的最短路径的长度（且 edgeTo[w] 的值即为该路径上的最后一条边）。

最优性条件和通用算法，给出了计算最短路径的思路，但是没有指定边的放松顺序。接下来学的 Dijkstra 算法、Bellman-Ford 算法和 DAG 有向无环图算法，主要区别在于：边的放松顺序不一样。

特点

• 环路
  最短路径不能包含环路，不管是负值环还是正值环。
• 唯一性
  最短路径并不是唯一的，最短路径树也不是唯一的。

Dijkstra 算法

定义

Dijkstra 算法类似 Prim 算法：构造的每一步都想这棵树中添加一条新的边。
首先将 distTo[s] 初始化为 0，distTo[] 其他元素初始化为正无穷。然后将 distTo[] 最小的非树顶点放松并加入树中，直到所有顶点都在树中或者所有的非树顶点的 distTo[] 值均为无穷大。

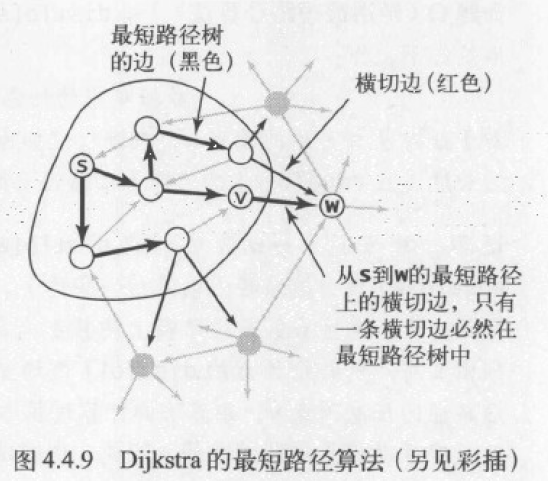
Dijkstra 算法能够解决边权重非负的加权有向图的单起点最短路径问题。边的放松顺序为：距离起点路径最短的顶点，该顶点指向邻接点的边。且整个算法过程中，每条边会被放松一次。

正确性证明

Dijkstra 算法每条边的放松，都是基于前驱顶点最短路径已经确定的前提下进行的。

不能处理负权重边的原因

Dijkstra 算法属于贪心算法，每次选的是当前能连到的边中权值最小的，并没有考虑到远处的边。在正权重图中这种贪心是对的，但是在负权重图中，远处的负权重边会影响当前能连到的权值最小值并不是最优解。
从上面的正确性证明中也可看出，每条边的放松，前驱顶点的最短路径必须是已经确定了的。但是如果存在负权重边，前驱顶点的最短距离将会可能会被后续的负权重边修改。

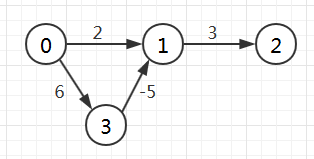
从示例中可以看出，根据 Dijkstra 算法，顶点 0 到顶点 2 的最短路径为：0 -> 1 -> 2，最短距离为 5。但是实际上，最短路径应该为 0 -> 3 -> 1 -> 2，因为存在负权重边，这条路径最短距离为 4. 所以存在负权重边的有向图， Dijkstra 算法计算出的最短路径并不准确。

疑问：在《算法 4》中给出的 DijkstraSP 实现中，只要去掉负权重边的判断，上图测试数据，算法最终还是可以准确计算出最短路径的。只是顶点 1 会两次入队，并更新顶点 1 和顶点 2 的最终最短路径。

动画演示

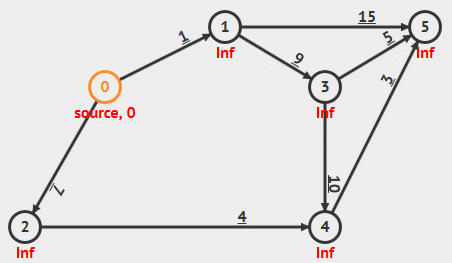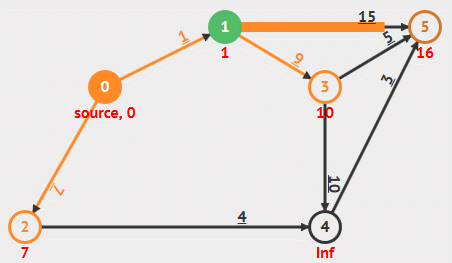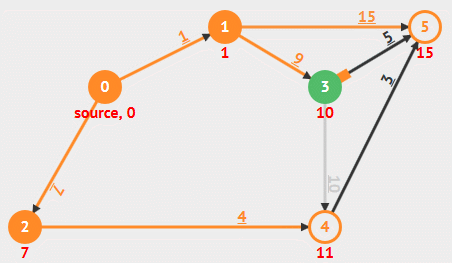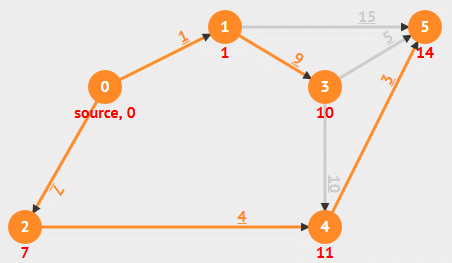
算法解析

• distTo[] 数组
  记录起点到当前顶点的，最短路径估计长度。
• edgeTo[] 数组
  记录起点到当前顶点最短路径上，最后一条边。也就是说前驱顶点到当前顶点的边。
• IndexMinPQ<Double> pq 索引最小优先队列
  索引为当前顶点，记录对应的最短路径估计（distTo）。使用索引最小优先队列的目的是，在边的松弛时，方便更新（降低）键值；最小值为距离起点路径最短的顶点。

public class DijkstraSP {
    private double[] distTo;
    private DirectedEdge[] edgeTo;
    private IndexMinPQ<Double> pq;
    
    public DijkstraSP(EdgeWeightedDigraph G, int s) {
        //疑问：如果去掉负权重边的判断，自测的几组包含负权重边的有向图
        // 是可以正确计算最短路径的，只是负权重边的顶点会重复入队
        for (DirectedEdge e : G.edges()) {
            if (e.weight() < 0)
                throw new IllegalArgumentException(
                    "edge " + e + " has negative weight");
        }

        distTo = new double[G.V()];
        edgeTo = new DirectedEdge[G.V()];

        //validateVertex(s);

        // 初始化所有顶点
        for (int v = 0; v < G.V(); v++)
            distTo[v] = Double.POSITIVE_INFINITY;
        distTo[s] = 0.0;
        // relax vertices in order of distance from s
        pq = new IndexMinPQ<Double>(G.V());
        pq.insert(s, distTo[s]);
        
        // 放松所有的边
        while (!pq.isEmpty()) {
            // 放松顺序：距离起点路径最短的顶点，该顶点指向邻接点的边
            int v = pq.delMin();
            for (DirectedEdge e : G.adj(v))
                relax(e);
        }
    }

    // relax edge e and update pq if changed
    private void relax(DirectedEdge e) {
        int v = e.from(), w = e.to();
        // 边的放松
        if (distTo[w] > distTo[v] + e.weight()) {
            distTo[w] = distTo[v] + e.weight();
            edgeTo[w] = e;
            
            // 索引优先队列降键值
            if (pq.contains(w)) pq.decreaseKey(w, distTo[w]);
            else                pq.insert(w, distTo[w]);
        }
    }
}

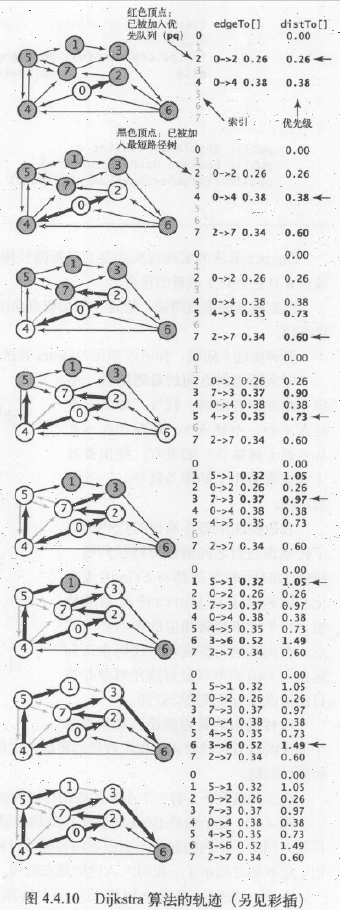
小结

• 权重
  Dijkstra 算法要求所有边的权重为非负值，但是可以包含有向环。
• 边的放松顺序
  放松顺序为：距离起点路径最短的顶点，该顶点指向邻接点的边。且整个算法过程中，每条边会被放松一次。
• 时间复杂度
  边的放松过程：优先队列的大小为 V 个顶点，插入或者降键值需要 logV ，需要放松所有的边即 E 条边。所以 Dijkstra 算法的时间复杂度为 O(ElogV) 。

参考文档

• 《算法：第四版》 第 4 章
• algs4: sp
• visualgo动画-Dijkstra实现