算法 - 最短路径：有向无环图

发表于 | 分类于 | 阅读次数

在计算最短路径时，Dijkstra 算法和 Bellman-Ford 算法都可以包含环，但是时间复杂度都较高。而有向无环图中，使用拓扑顺序放松边，能非常高效解决单点路径问题。

概念

加权有向无环图最短路径算法：

  • 能够在线性时间内解决单点路径问题
  • 能够处理负权重的边
  • 能够解决相关问题，例如找到最长的路径

其特点是：无环，权重可正可负，但是不能包含环。

算法定义

首先将 distTo[s] 初始化为 0，其他 distTo[] 元素初始化为无穷大，然后一个一个地按照拓扑顺序放松所有顶点。

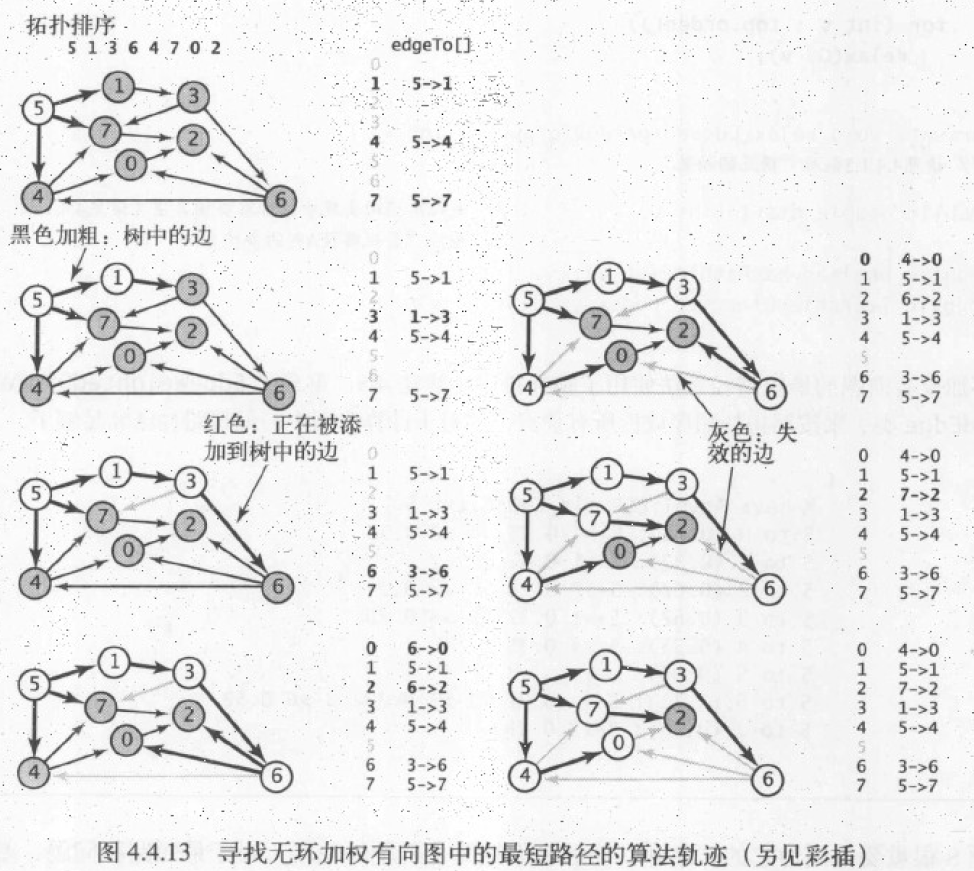
0100-spt-dag-trace.png

按照拓扑排序放松所有顶点，能在和 E+V 成正比的时间内解决无环加权有向图的单点路径问题。

动画演示

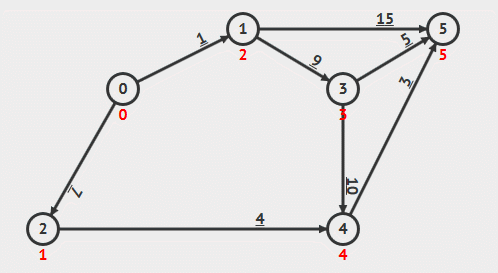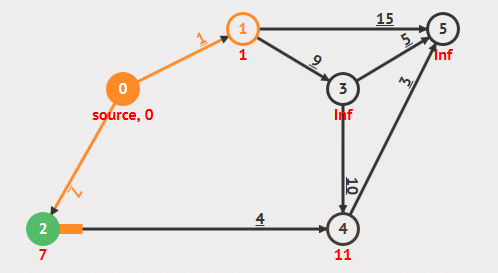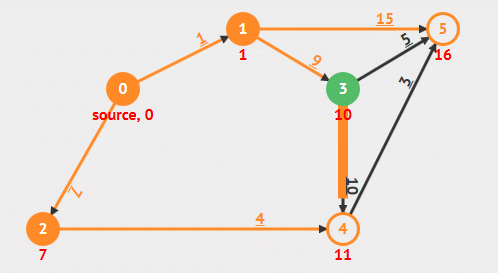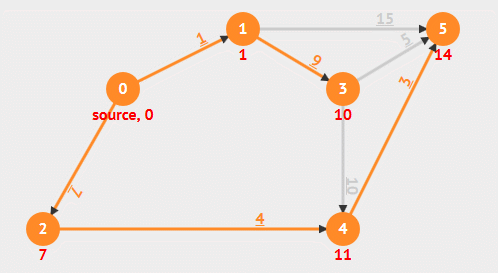
0100-spt-dag.gif

算法解析

  • double[] distTo 数组
    记录起点到当前顶点的，最短路径估计长度。
  • DirectedEdge[] edgeTo 数组
    记录起点到当前顶点最短路径上，最后一条边。也就是说前驱顶点到当前顶点的边。 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
public class AcyclicSP {
    private double[] distTo;
    private DirectedEdge[] edgeTo;

    public AcyclicSP(EdgeWeightedDigraph G, int s) {
        distTo = new double[G.V()];
        edgeTo = new DirectedEdge[G.V()];

        //validateVertex(s);

        // 初始化
        for (int v = 0; v < G.V(); v++)
            distTo[v] = Double.POSITIVE_INFINITY;
        distTo[s] = 0.0;

        // visit vertices in topological order
        // 拓扑排序顶点，并判断是否有环
        Topological topological = new Topological(G);
        if (!topological.hasOrder())
            throw new IllegalArgumentException("Digraph is not acyclic.");
        
        // 按照拓扑顺序取出顶点
        for (int v : topological.order()) {
            for (DirectedEdge e : G.adj(v))
                relax(e);
        }
    }

    // relax edge e
    private void relax(DirectedEdge e) {
        int v = e.from(), w = e.to();
        if (distTo[w] > distTo[v] + e.weight()) {
            distTo[w] = distTo[v] + e.weight();
            edgeTo[w] = e;
        }
    }
}

小结

  • 权重
    边的权重可正可负，有向图不能包含环。
  • 边的放松顺序
    按照顶点的拓扑顺序，放松所有的边；且所有的边只会被放松一次。
  • 时间复杂度
    V 个顶点，E 条边的有向无环图，拓扑排序时间复杂度为 O(E+V)；而根据拓扑顺序放松所有的边为 O(E)；所以总的时间复杂度为 O(E+V) 。

最短路径算法对比

Dijkstra 算法

  • 特点：支持环，仅能处理权重全为正的有向图
  • 时间复杂度为 O(ElogV)
  • 边的放松顺序
    小根堆取出距离起点距离最近的顶点，依次放松该顶点指向邻接点的边；且每条边只会被放松一次。

Bellman-Ford 算法

  • 特点：支持环，权重正或负都能处理，但有向图中不能存在负权重环（如果存在，最短路径树的计算会被无限循环放松）
  • 时间复杂度为 O(EV)
  • 边的放松顺序
    原始 Bellman-Ford 算法：以任意顺序放松边，放松 V 轮；SPFA 基于队列改进型算法：当 distTo[w] 值发生变化的顶点进入队列，以 FIFO 的方式放松该顶点指向邻接点的边。

DAG 有向无环图算法

  • 特点：不支持环，权重正或负都能处理
  • 时间复杂度为 O(E+V)
  • 边的放松顺序
    按照顶点的拓扑顺序，放松所有的边；且所有的边只会被放松一次。

支持环：仅仅表示有向图中可以有环存在；但最短路径树中是不可能存在环的（不管是正权重环还是负权重环）。三个算法的主要区别在于边的放松顺序不同。

参考文档

0%