算法 - 子字符串匹配 KMP 算法

发表于 | 分类于 | 阅读次数

介绍子字符串匹配算法：暴力匹配算法，KMP 算法。

概念

定义

字符串匹配问题的形式定义：

  • 文本 Text 是一个长度为 n 的数组 T[1..n]
  • 模式 Pattern 是一个长度为 m 且 m≤n 的数组 P[1..m]
  • T 和 P 中的元素都属于有限的字母表 Σ 表的字符；比如：Σ={0,1} 或者 Σ={a,b,...,z}。P, T 通常称为字符串

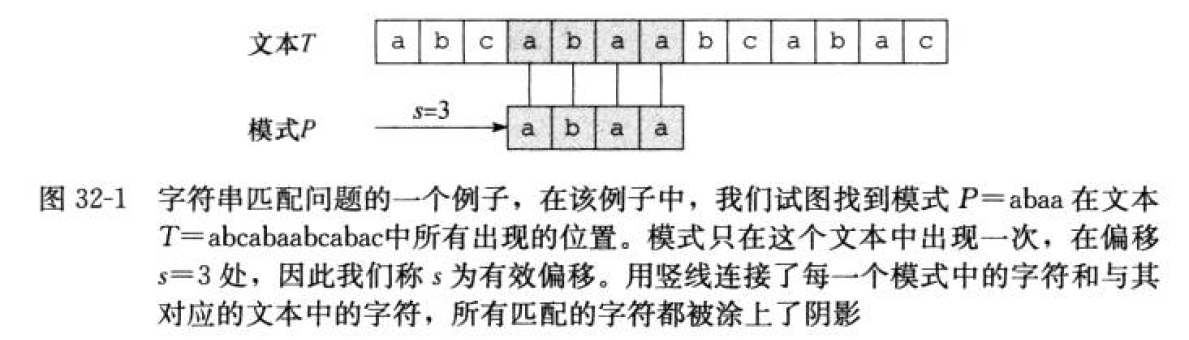
如果 0≤s≤n-m，并且 T[s+1..s+m] = P[1..m]，即对 1≤j≤m，有 T[s+j] = P[j]，那么称模式 P 在文本 T 中出现，且位移为 s。称 s 是一个有效偏移；如果 s 不出现则称它为无效偏移。

0102-strings-search-definition.png

时间复杂度

字符串匹配算法通常分为两个步骤：预处理 Preprocessing 和匹配 Matching 。算法的总运行时间为预处理和匹配两个阶段所耗时间的总和。

暴力匹配算法

朴素的字符串匹配算法 Naive String Matching Algorithm ，又称为暴力匹配算法 Brute Force Algorithm 。

算法实现

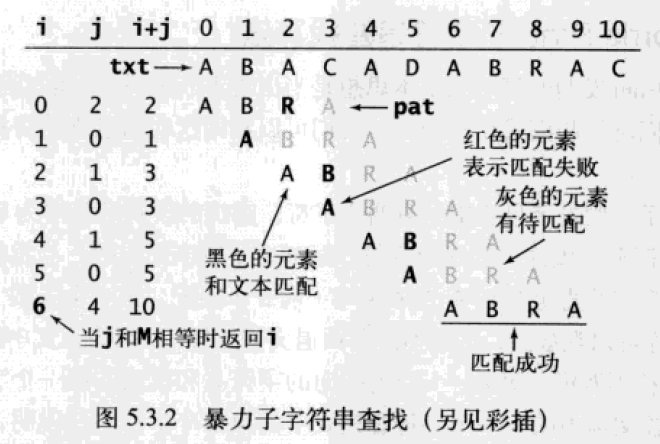
使用下标 i 记录文本位置；使用下标 j 记录模式位置。从文本和模式的首字母开始比较，直到整个模式匹配，则返回文本位置。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public static int search(String pat, String txt){
    int M = pat.length();
    int N = txt.length();
    int i =0, j = 0;
    
    while(i < N && j < M){
        if (txt.charAt(i) == pat.charAt(j)) {
            i++;
            j++;
        } else {
            i = i - j + 1;
            j = 0;
        }
    }
    
    if (j == M) return i - j;   // 找到匹配
    else return -1;             // 未找到匹配
}

0102-strings-search-brute-force.png

时间复杂度

暴力匹配算法没有预处理步骤，在最坏情况下，在长度为 N 的文本中查找长度为 M 的模式，时间复杂度为 O(NM) 。

0102-strings-search-brute-force-worst.png

KMP 算法基础概念

KMP: Knuth-Morris-Pratt 子字符串查找算法的基本思想是：当出现不匹配时，已经能知晓一部分文本内容（因为在匹配失败前这部分文本内容已经和模式相匹配），利用这些信息避免将下标回退到这些已知字符之前。

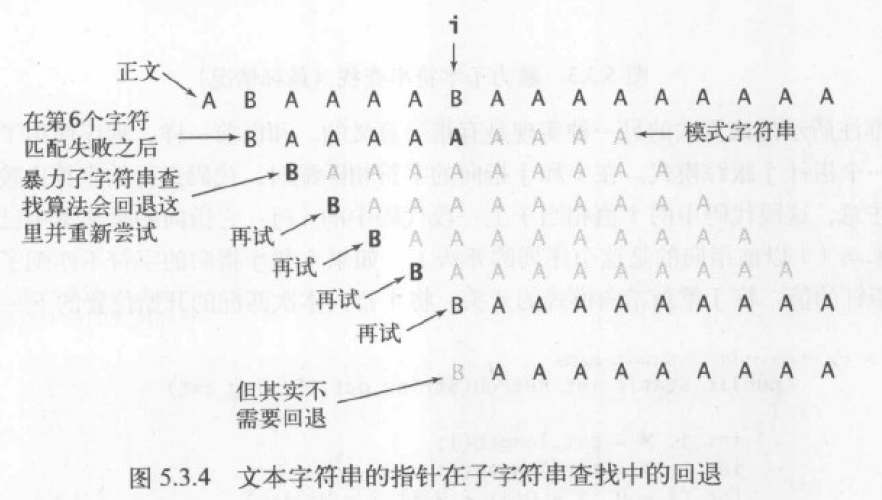
0102-strings-search-kmp.png

《算法 4》中的 KMP 算法使用了有限状态机 DFA[][] 来计算下标回退的位置。我们这里参考《算法导论 3》中更通用的算法，使用模式的前后缀来计算下标。

伪代码

《算法导论》中的伪代码，其中当出现不匹配时， π 数组记录了不匹配字符对应的移动距离，这个值是模式向右移动的距离。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
KMP-MATCHER(T,P)
    n=T.length              // 文本长度
    m=P.length              // 模式长度
    π=COMPUTE-PREFIX-FUNCTION(P)
    q=0                     // 字符串匹配个数
    for i=1 to n            // 从左往右扫描文本
        while q>0 and P[q+1]≠T[i]
            q=π[q]          // 下个字符不匹配
        if P[q+1] == T[i]
            q=q+1           // 下个字符匹配
        if q == m           // 模式完全匹配？
            print "Pattern occurs with shift" i-m 
        q=π[q]              // 从下一个位置开始查找

COMPUTE-PREFIX-FUNCTION(P)
    m=P.length
    let π[1..m] be a new array
    π[1]=0
    k=0
    for q=2 to m
        while k>0 and P[k+1]≠P[q]
            k=π[k]
        if P[k+1] == P[q]
            k=k+1
        π[q]=k
    return π

next 数组

先了解两个定义：

  • 前缀：字符串中去掉最后一个字符后，全部头部字符串组合
  • 后缀：字符串中去掉第一个字符，全部尾部字符串组合

比如：字符串 bread，其前缀和后缀分别为：

  • 前缀：b, br, bre, brea
  • 后缀：read, ead, ad, d

根据以上定义，我们计算模式 ABCDABD 中，每个子串前后缀的最长共有元素长度：

模式的子串 前缀 后缀 最长共有元素 长度
A 空集 空集 无 0
AB A B 无 0
ABC A, AB BC, C 无 0
ABCD A, AB, ABC BCD, BC, D 无 0
ABCDA A, AB, ABC, ABCD BCDA, CDA, CD, A A 1
ABCDAB A, AB, ABC, ABCD, ABCDA BCDAB, CDAB, DAB, AB, B AB 2
ABCDABD A, AB, ABC, ABCD, ABCDA, ABCDAB BCDABD, CDABD, DABD, ABD, BD, D 无 0

最长共有元素长度，表示有相同前后缀的长度。这也是 KMP 算法的核心，当出现不匹配字符时，利用前面已知的已经匹配的字符，不需要把文本字符串下标回退，而是利用具有相同前后缀信息，直接将模式向后移动。

next 数组：记录了每个元素前的子串前后缀最长共有元素长度，其中 next 数组第一位默认为 -1 。（而模式本身对应的最长共有元素长度舍弃掉）

0102-strings-search-kmp-next-array.png

模式移动位数

移动位数 = 失配字符所在位置 - 失配字符对应的 next 值。（字符位置从 0 开始计数）

使用下标 j 记录模式中不匹配字符所在位置，该位置对应的 next[j]=k ，即前后缀最长共有元素长度为 k。那么移动位数为：j - next[j] 。我们用下图来表示：

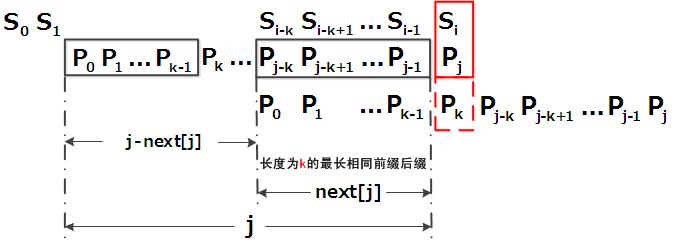
0102-strings-search-kmp-next-value.jpg

模式在 Pj 和文本 Si 位置匹配失败，此时模式的前缀和后缀共有元素为 P0 P1 ... Pk-1 = Pj-k Pj-k+1 ... Pj-1，即有 k 个最长共有元素 next[j] = k 。模式向后移动位数为 j - next[j] ，让模式的 Pk 位置字符和文本 Si 位置字符继续匹配。也就是说：模式的下个比较的位置为 j=k=next[j] 。

next[j] 的实际意义为：模式匹配过程中，如果该位置字符不匹配，模式从 next[j] 位置开始和文本的第 i 个位置继续比较。也就是说 KMP 算法中，为确保文本不用回退，模式整体向后移动 j-next[j] 位。

图解

文本：BBC ABCDAB ABCDABCDABDE ；模式：ABCDABD 。

  • 子字符串匹配从文本和模式的第一个字符开始比较，直到出现不匹配字符
    0102-strings-search-kmp-graph-1.png
  • 如果是暴力匹配算法，存在文本下标回退
    0102-strings-search-kmp-graph-2.png
  • KMP 算法，仅将模式向后移动
    模式在第 6 位字符 D 出现不匹配，对应的 next 值为 2，所以模式移动位数为 6-2=4 ；模式向后移动 4 位，继续匹配。
    0102-strings-search-kmp-graph-3.png
  • 继续比较中，模式中字符 C 与文本的空格不匹配
    模式在第 2 位字符 C 出现不匹配，对应的 next 值为 0，所以模式移动位数为 2-0=2 ；模式向后移动 2 位，继续匹配。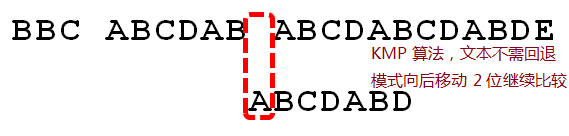
    0102-strings-search-kmp-graph-4.png
  • 继续比较中，模式中字符 A 与文本的空格不匹配
    此次比较模式的第一个字符就不匹配，模式和文本同时向后移动一位，继续比较。
  • 继续比较中，直到出现不匹配字符
    模式在第 6 位字符 D 和文本中的字符 C 不匹配，对应的 next 值为 2，模式向后移动 4 位，继续匹配。
    0102-strings-search-kmp-graph-5.png
  • 模式向后移动 4 位后，匹配成功
    0102-strings-search-kmp-graph-6.png

KMP 算法解析

next 数组计算

next 数组第一位默认为 -1，假设已知 0...j 个字符对应的 next 数组值，其中第 j 个字符前的子串，其前后缀最长共有元素长度为 k ， 即 next[j]=k。那么：如何计算第 j+1 个字符串的 next ？

  • P[k] == P[j]

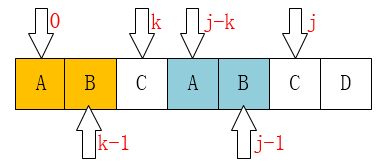
0102-strings-search-kmp-next-calculator-1.png

当 P[k] == P[j] 时，意味着第 j+1 个字符前的子串，其前后缀最长共有元素多了一位，即 next[j+1] = next[j]+1 = k+1 。

  • P[k] ≠ P[j]

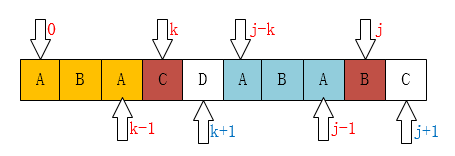
0102-strings-search-kmp-next-calculator-2.png

因为前 k-1 个字符是相同的，而第 k 位和 j 位字符不匹配。我们换个思路来看待这个问题：将模式的前 k+1 个字符比作新的模式，原模式去掉新模式后剩余字符串比作新的文本。这样类比后，可以看作一个新的模式和文本匹配问题了。

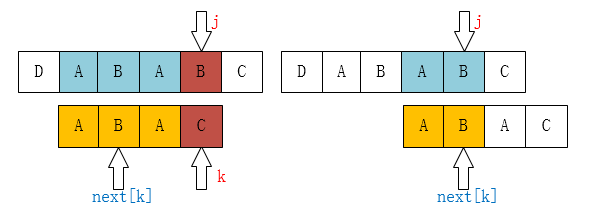
0102-strings-search-kmp-next-calculator-3.png

而 next[0...k] 是已知的，根据 KMP 算法，第 k 个元素出现不匹配，将新的模式整体向后移动，即新模式从 k=next[k] 的位置重新和 j 比较。这是一个递归过程，直到出现 P[k] == P[j] 或者 k=-1 为止。其中：
如果 P[k] == P[j] ， 则 next[j+1]=next[k]+1=k+1；
如果 k=-1 ，则表示新模式的第一个字符就和新文本的第 j 位不相等，匹配结束没有共有元素，next[j+1]=0=k+1。

next 数组计算分为两种情况：k=-1 或者 P[k] == P[j] 时，next[j+1]=k+1；其他情况即出现不匹配时，使用最大子串 k=next[k] 继续比较，即从第 next[k] 处开始继续比较。

k=next[k] 的意义：表示 k 个字符串内部前后缀最大共有元素长度，使用该子串继续去匹配：

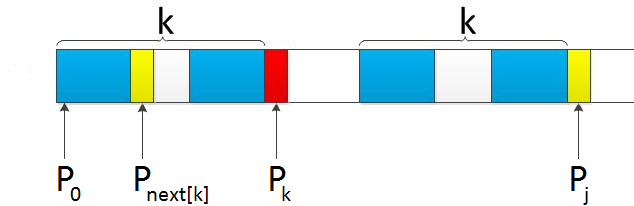
0102-strings-search-kmp-next-calculator-4.png

算法实现

算法分为两部分：预处理和匹配搜索。预处理步骤用来计算 next 数组；匹配步骤用来从文本中搜索模式字符串。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
private int next[];
// 计算 next 数组
private void KMPCLRNext(String pattern) {
    int m = pattern.length();
    next = new int[m];
    next[0] = -1;
    int j = 0, k = -1;

    while (j < m - 1) {
        // k 为 -1，表示不匹配，没有共有元素
        // 或者第 k 个位置的字符和第 j 个位置字符相等时
        // next[j+1]=k+1
        if (k == -1 || pattern.charAt(j) == pattern.charAt(k)) {
            next[++j] = ++k;
        } else {
        // 如果出现不匹配，从第 next[k] 位置继续匹配
            k = next[k];
        }
    }
}

// 文本中搜索模式字符串
private int KMPCLRSearch(String text, String pattern) {
    KMPCLRNext(pattern);

    int n = text.length();
    int m = pattern.length();

    int i = 0, j = 0;
    while (i < n && j < m) {
        // j 为 -1 时，表示模式的第一个字符和文本当前位置不匹配
        // 或者文本第 i 个位置字符和模式第 j 个位置字符匹配
        // 这两种情况：文本和模式都同时向后移动一位
        if (j == -1 || text.charAt(i) == pattern.charAt(j)) {
            i++;
            j++;
        } else {
        // 如果模式不是在第一个字符出现的不匹配，模式向后移动 j-next[j] 位 
        // 即模式从第 next[j] 位置处和文本第 i 个位置字符继续匹配
            j = next[j];
        }
    }

    // 匹配成功
    if (j == m)
        return i - j;
    else
        return -1;
}

参考：algs4:kmp

时间复杂度

KMP 算法预处理步骤，需要遍历模式所有字符串（长度为 m），时间复杂度为 O(m)；搜索匹配阶段，需要遍历文本所有字符串（长度为 n），时间复杂度为 O(n)。所以整个算法时间复杂度为 O(n+m) 。

JDK 中 String.indexOf 算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
static int indexOf(char[] source, int sourceOffset, int sourceCount,
        char[] target, int targetOffset, int targetCount,
        int fromIndex) {
    if (fromIndex >= sourceCount) {
        return (targetCount == 0 ? sourceCount : -1);
    }
    if (fromIndex < 0) {
        fromIndex = 0;
    }
    if (targetCount == 0) {
        return fromIndex;
    }

    char first = target[targetOffset];
    int max = sourceOffset + (sourceCount - targetCount);

    for (int i = sourceOffset + fromIndex; i <= max; i++) {
        /* Look for first character. */
        if (source[i] != first) {
            while (++i <= max && source[i] != first);
        }

        /* Found first character, now look at the rest of v2 */
        if (i <= max) {
            int j = i + 1;
            int end = j + targetCount - 1;
            for (int k = targetOffset + 1; j < end && source[j]
                    == target[k]; j++, k++);

            if (j == end) {
                /* Found whole string. */
                return i - sourceOffset;
            }
        }
    }
    return -1;
}

从算法实现可以看出：indexOf 使用了暴力匹配算法。

参考文档

0%