算法 - 字符串排序算法

发表于 | 分类于 | 阅读次数

介绍字符串的几种排序算法：键索引计数法、低位优先排序、高位优先排序、三向字符串快速排序。

键索引计数法

概念

键索引计数法：适合小整数键的简单排序。它的实现步骤为如下四步：

  • 频率统计
  • 频率转换为索引
  • 数据分类
  • 回写

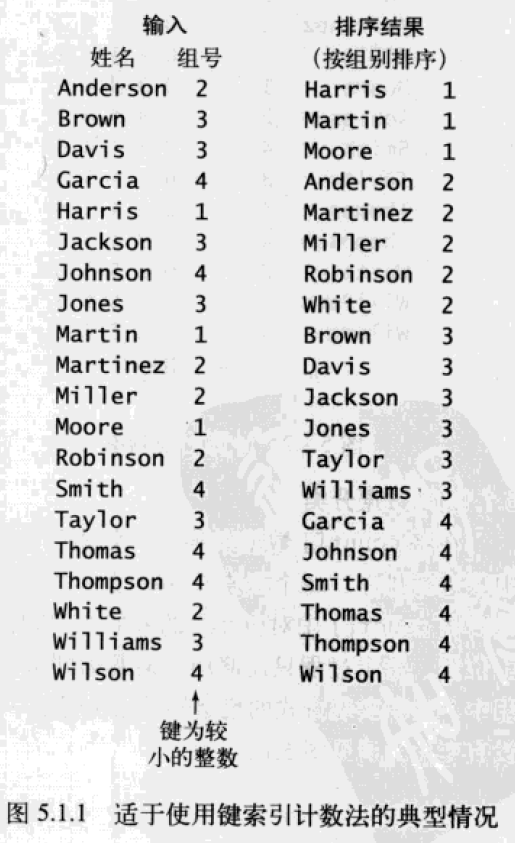
0104-strings-sort-key-index-count.png

算法实现

N 个字符串；R 个键值，键值范围 [0, R) 从 0 到 R-1 。

  • 数组 a[]
    存储待排序元素 item 的数组，长度为 N，item 记录字符串和对应的键值。
  • 整型数组 count[]
    数组长度为 R+1，为什么要多两个？其中 count[0] 和 count[R] 有特殊作用：
    在频率统计中，count[r] 记录键 r-1 出现的频率，即从 count[1] 开始记录键值出现的频率。其中：count[0] 无作用，默认设置为 0；count[R] 记录键 R-1 出现的频率。
    在频率转换为索引中，count[r] 记录键 r 在预期排序结果的起始索引位置；任意给定键 r 的起始索引位置为所有较小键出现频率之和，即 count[r+1] += count[r]。其中：count[0] 记录键 0 的起始索引；count[R] 无实际作用，记录 a[] 的长度。
    在数据分类中，count[r] 记录了*下一个键 r *的索引位置，即 count[a[i].key()]++ 。正常情况下，分类结束后的 count[r] 和分类前的 count[r+1] 值相等。
  • 辅助数组 aux[]
    存储排序后的值。 a[i] 元素在 aux[] 中的位置，由 a[i] 的键值 r 在 count[] 中索引值决定，在移动之后 count[] 中对应索引值加 1，确保 count[r] 总是下一个键为 r 的元素在 aux[] 中的索引位置。 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
// R 个键值，n 个字符串
int[] count = new int[R+1];

// 频率统计
for (int i = 0; i < n; i++)
    count[a[i].key() + 1]++;

// 频率转换为索引
for (int r = 0; r < R; r++)
    count[r+1] += count[r];

// 数据分类
for (int i = 0; i < n; i++)
    // 数据移动时，同步更新 count[] 的索引
    aux[count[a[i].key()]++] = a[i];

// 回写
for (int i = 0; i < n; i++)
    a[i] = aux[i];

图解

  • 频率统计
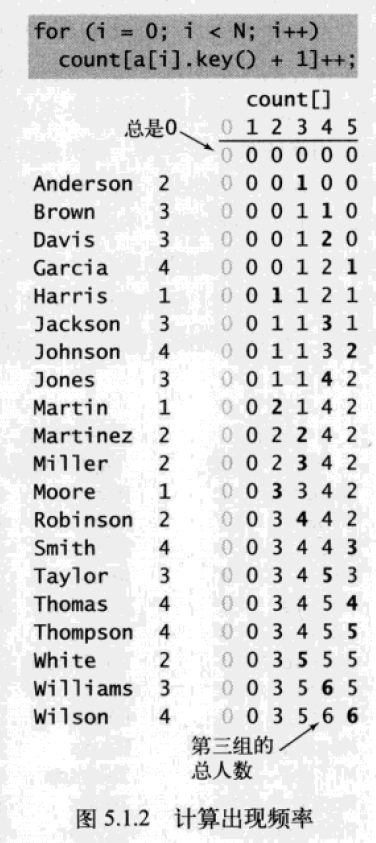
    0104-strings-sort-key-index-count-step-1.png
  • 频率转换为索引
    0104-strings-sort-key-index-count-step-2.png
  • 数据分类
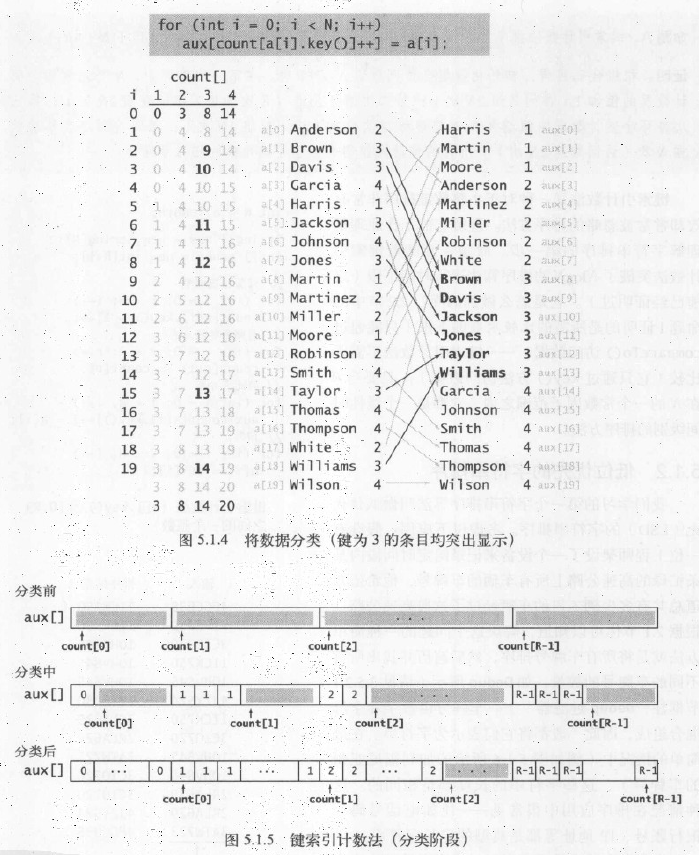
    0104-strings-sort-key-index-count-step-3.png

小结

键索引计数法是一种对于小整数键排序非常有效，但容易被忽略的排序算法。被排序字符串时等长字符串，可以在线性时间内完成排序。
注意：键索引计数法不会对相同键值的字符串做排序，仅仅按照键值排序排序字符串。

LSD 低位优先字符串排序

概念

LSD: Least Significant Digit radix sorts，低位优先字符串排序算法，要求字符串时定长的（即所有被排序字符串长度相同），能够稳定地将定长字符串排序。
思路：从右向左（即低位优先）依次将字符作为键值排序，通常取扩展 ASCII 码长度作为键的个数（256 个）。定长字符串长度为 W，只需要使用键索引计数法排序 W 遍，就可以得到最终排序结果了。

0104-strings-sort-lsd.png

算法实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
public static void sort(String[] a, int w) {
    int n = a.length;
    int R = 256;   // extend ASCII alphabet size
    String[] aux = new String[n];

    // n 个字符串，R 个键值，字符串为定长 W 
    // 低位优先，即从右向左一次将字符作为键值排序
    for (int d = w-1; d >= 0; d--) {
        // 键索引计数法  
        // sort by key-indexed counting on dth character

        // compute frequency counts
        int[] count = new int[R+1];
        for (int i = 0; i < n; i++)
            // chatAt(d) 将字符作为键值
            count[a[i].charAt(d) + 1]++;

        // compute cumulates
        for (int r = 0; r < R; r++)
            count[r+1] += count[r];

        // move data
        for (int i = 0; i < n; i++)
            aux[count[a[i].charAt(d)]++] = a[i];

        // copy back
        for (int i = 0; i < n; i++)
            a[i] = aux[i];
    }
}

参考：algs4: lsd

图解

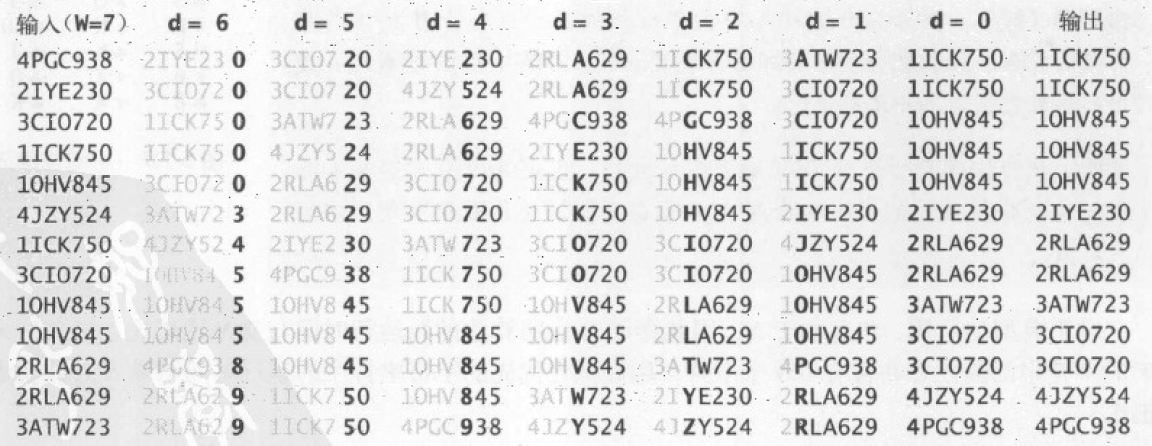
0104-strings-sort-lsd-samples.png

小结

对于 N 个定长为 W 的字符串，无论 N 有多大，都只需要遍历 W 次就能实现排序，排序时间也是线性的。

MSD 高位优先字符串排序

概念

MSD: Most Significant Digit radix sorts，高位优先字符串排序算法，可以实现通用字符串排序（即字符串长度可以不同），从左向右遍历所有字符。
思路：首先用键索引计数法将所有字符串按照首字母排序，然后（递归地）再将每个首字母所对应的子数组排序（忽略首字母，因为每一类中的所有字符串首字母是相同的）。
和快速排序一样，高位优先字符串排序会将数组切分为能够独立排序的子数组来完成排序任务，但它的切分会为每个首字母得到一个子数组，而不是像快速排序中产生固定的切分。

0104-strings-sort-msd.png

count[] 数组的含义

字符串末尾的约定：对于长度不等的字符串，当到达末尾时，指定位置为 -1，也就是说认为末尾字符为 count[0] 。

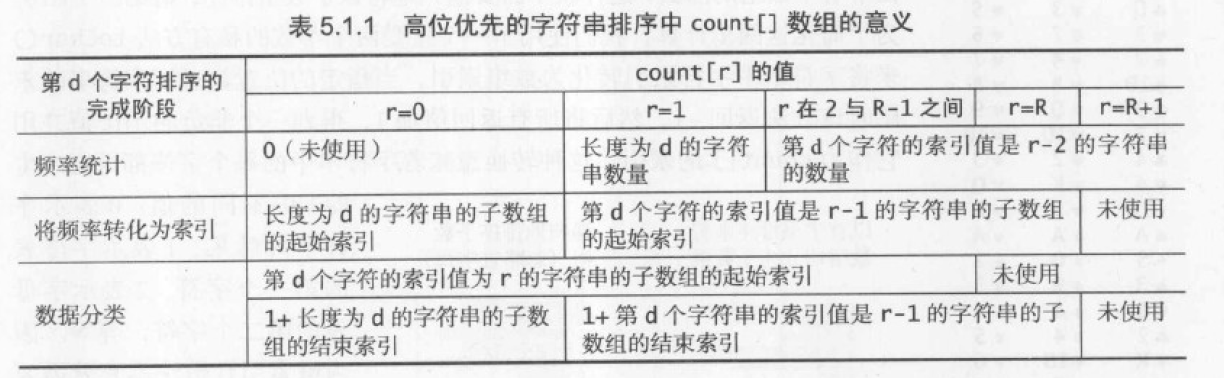
0104-strings-sort-msd-count.png

小型子数组

高位优先字符串排序的基本思想：在一般应用中，只需检查若干个字符就能完成所有字符串的排序。也就是说，这种方法能快速地将需要排序的数组切分为较小的数组。小型子数组对于高位优先的字符串排序性能至关重要。对于小型子数组，需要将排序算法切换为插入排序，减少过多的微型数组排序。

算法实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
public class MSD {
    private static final int R = 256;   // extended ASCII alphabet size
    private static final int CUTOFF =  15; // cutoff to insertion sort

    // do not instantiate
    private MSD() { } 

    public static void sort(String[] a) {
        int n = a.length;
        String[] aux = new String[n];
        sort(a, 0, n-1, 0, aux);
    }

    // return dth character of s, -1 if d = length of string
    // 如果到达字符串末尾，返回 -1
    private static int charAt(String s, int d) {
        assert d >= 0 && d <= s.length();
        if (d == s.length()) return -1;
        return s.charAt(d);
    }

    // sort from a[lo] to a[hi], starting at the dth character
    private static void sort(String[] a, int lo, int hi, 
        int d, String[] aux) {

        // cutoff to insertion sort for small subarrays
        if (hi <= lo + CUTOFF) {
            // 小型子数组切换为插入排序
            insertion(a, lo, hi, d);
            return;
        }

        // 键索引计数法四部曲
        // compute frequency counts
        int[] count = new int[R+2];
        for (int i = lo; i <= hi; i++) {
            int c = charAt(a[i], d);
            count[c+2]++;
        }

        // transform counts to indicies
        for (int r = 0; r < R+1; r++)
            count[r+1] += count[r];

        // distribute
        for (int i = lo; i <= hi; i++) {
            int c = charAt(a[i], d);
            aux[count[c+1]++] = a[i];
        }

        // copy back
        for (int i = lo; i <= hi; i++) 
            a[i] = aux[i - lo];


        // recursively sort for each character (excludes sentinel -1)
        // 递归实现
        for (int r = 0; r < R; r++)
            sort(a, lo + count[r], lo + count[r+1] - 1, d+1, aux);
    }

    // insertion sort a[lo..hi], starting at dth character
    // 插入排序
    private static void insertion(String[] a, int lo, int hi, int d) {
        for (int i = lo; i <= hi; i++)
            for (int j = i; j > lo && less(a[j], a[j-1], d); j--)
                exch(a, j, j-1);
    }

    // exchange a[i] and a[j]
    private static void exch(String[] a, int i, int j) {
        String temp = a[i];
        a[i] = a[j];
        a[j] = temp;
    }

    // is v less than w, starting at character d
    private static boolean less(String v, String w, int d) {
        // assert v.substring(0, d).equals(w.substring(0, d));
        for (int i = d; i < Math.min(v.length(), w.length()); i++) {
            if (v.charAt(i) < w.charAt(i)) return true;
            if (v.charAt(i) > w.charAt(i)) return false;
        }
        return v.length() < w.length();
    }
}

参考：algs4: msd

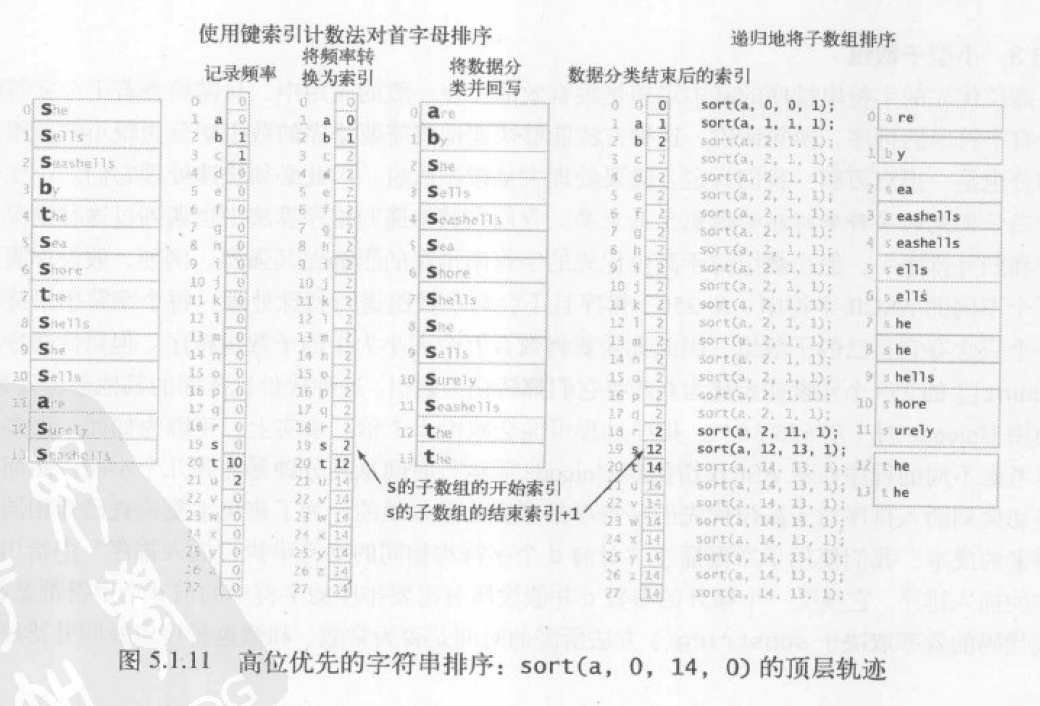
0104-strings-sort-msd-sort-trace.png

图解

0104-strings-sort-msd-sample.png

小结

高位优先字符串排序不会处理等值键数组。如果相同的子字符串出现过多，也不会切换排序算法，那么递归方法会检查相同键中的每一个字符。总体来讲，高位优先算法能很好的解决随机字符串的排序。

三向字符串快速排序

概念

三向字符串快速排序 Three-way string quicksort ：根据键的首字母进行三向切分，仅在中间子数组中的下一个字符（因为键的首字母都与切分字符相等）继续递归排序。

0104-strings-sort-quick-3string.png

小型子数组

在所有递归算法中，都可以通过对小型子数组进行特殊处理来提高效率。三向字符串快速排序和高位优先字符串排序一样，对于小型子数组会切换到插入排序算法。

算法实现

为了避免数组已经有序或接近有序的最坏情况，排序前先将数组随机打乱或者将第一个元素和一个随机位置的元素交换，以得到一个随机的切分元素。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
public class Quick3string {
    private static final int CUTOFF =  15;   // cutoff to insertion sort

    // do not instantiate
    private Quick3string() { } 

    public static void sort(String[] a) {
        // 随机打乱数组
        StdRandom.shuffle(a);
        sort(a, 0, a.length-1, 0);
    }

    // return the dth character of s, -1 if d = length of s
    // 如果到达字符串末尾，返回 -1
    private static int charAt(String s, int d) { 
        assert d >= 0 && d <= s.length();
        if (d == s.length()) return -1;
        return s.charAt(d);
    }

    // 3-way string quicksort a[lo..hi] starting at dth character
    private static void sort(String[] a, int lo, int hi, int d) { 

        // cutoff to insertion sort for small subarrays
        if (hi <= lo + CUTOFF) {
            // 小型子数组切换为插入排序
            insertion(a, lo, hi, d);
            return;
        }

        // 对指定位置字符进行快速排序
        int lt = lo, gt = hi;
        int v = charAt(a[lo], d);
        int i = lo + 1;
        while (i <= gt) {
            int t = charAt(a[i], d);
            if      (t < v) exch(a, lt++, i++);
            else if (t > v) exch(a, i, gt--);
            else              i++;
        }

        // a[lo..lt-1] < v = a[lt..gt] < a[gt+1..hi]. 
        // 递归实现
        sort(a, lo, lt-1, d);
        if (v >= 0) sort(a, lt, gt, d+1);
        sort(a, gt+1, hi, d);
    }

    // sort from a[lo] to a[hi], starting at the dth character
    private static void insertion(String[] a, int lo, int hi, int d) {
        for (int i = lo; i <= hi; i++)
            for (int j = i; j > lo && less(a[j], a[j-1], d); j--)
                exch(a, j, j-1);
    }

    // exchange a[i] and a[j]
    private static void exch(String[] a, int i, int j) {
        String temp = a[i];
        a[i] = a[j];
        a[j] = temp;
    }

    // is v less than w, starting at character d
    private static boolean less(String v, String w, int d) {
        assert v.substring(0, d).equals(w.substring(0, d));
        for (int i = d; i < Math.min(v.length(), w.length()); i++) {
            if (v.charAt(i) < w.charAt(i)) return true;
            if (v.charAt(i) > w.charAt(i)) return false;
        }
        return v.length() < w.length();
    }
}

参考：algs4: Quick3string

图解

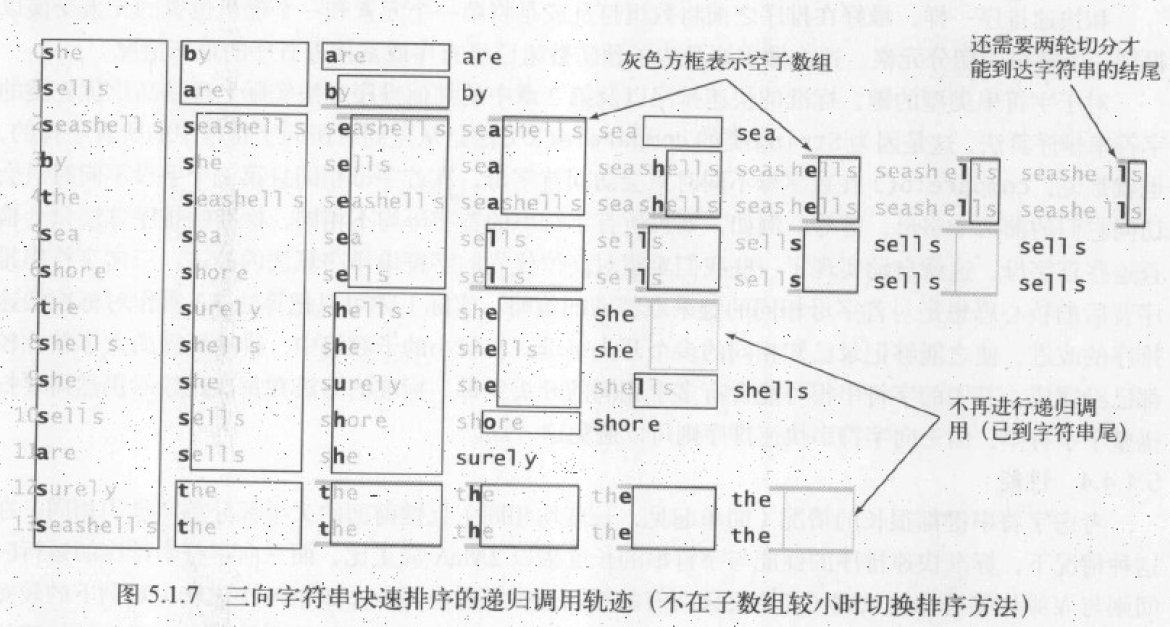
0104-strings-sort-quick-3string-samples.png

小结

高位优先字符串排序可能会创建大量（空）子数组，而三向字符串快速排序的切分总是只有三个。因此三向字符串快速排序能够很好地处理等值键、有较长公共前缀的键、取值范围较小的键和小数组等，所有高位优先字符串排序算法不擅长的各种情况。和普通快速排序一样，三向字符串快速排序也不需要额外的空间（除了递归所需的隐式栈调用）。

小结

各种字符串排序算法的性能特点：

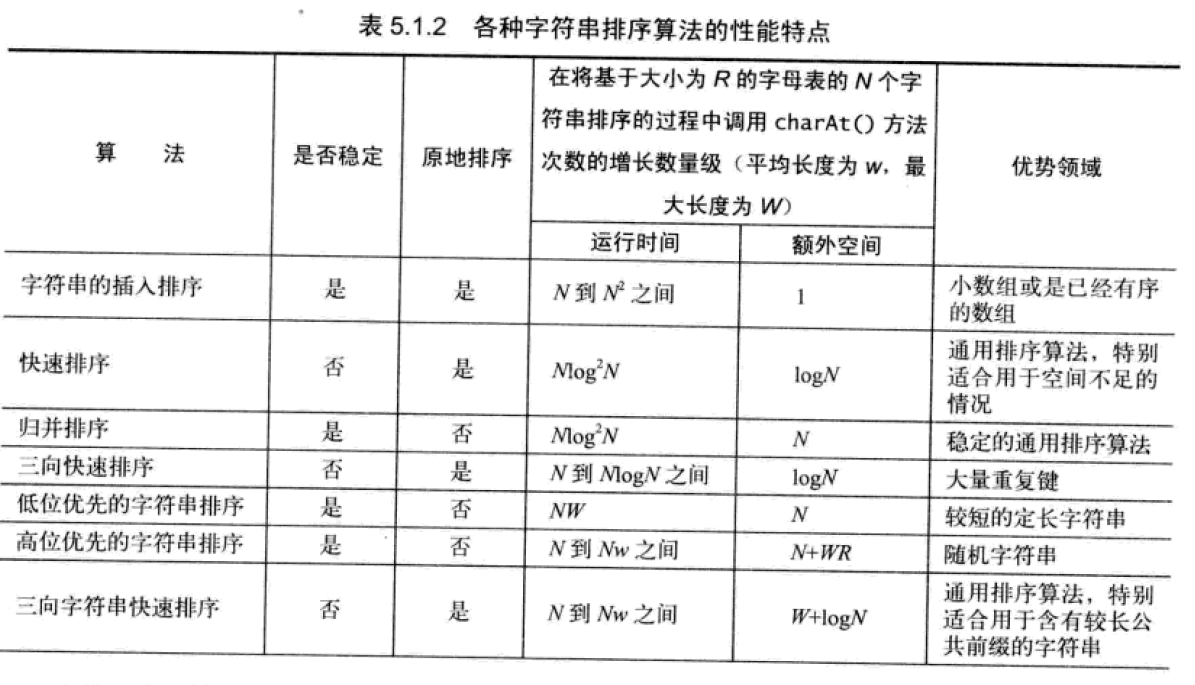
0104-strings-sort-summary.png

参考文档

  • 《算法：第四版》 第 5 章
0%